|
Was ist ein regelmäßiges
Sechseck?
|
Ein regelmäßiges Sechseck oder Hexagon ist ein Vieleck mit
sechs Ecken,
sechs gleich langen Seiten und
sechs gleich großen Innenwinkeln. |
Auf dieser Seite heißt das regelmäßige Sechseck meist
einfach Sechseck.
Konstruktion eines Sechsecks
top
... ...
|
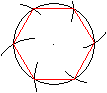
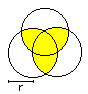
Man zeichnet einen Kreis und trägt auf dem Kreisbogen sechsmal
den gleichen Radius ab. Die Verbindungslinien der Schnittpunkte bilden
ein Sechseck.
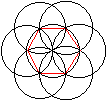
Zeichnet man die vollen Kreise, entsteht eine Rosette (rechts). |
... ...
|
Größen des Sechsecks
top
Ein regelmäßiges Sechseck ist im Allgemeinen durch die Seitenlänge
a
gegeben.
Daraus lassen sich der Flächeninhalt A, der Umfang
U,
der Radius des Umkreises R, der Radius des Inkreises r und
die Diagalen
d und e berechnen.
... ... |
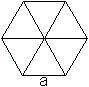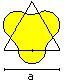
Am besten wählt man zur Herleitung die Aussage, dass das Sechseck
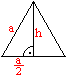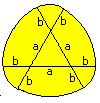
von sechs gleichseitigen Dreiecken gebildet wird. Man verwendet dann die
Formel für die Höhe des gleichseitigen Dreiecks. Nach dem Satz
des Pythagoras ist a²=h²+(a/2)² oder h = (1/2)sqrt(3)a. |
... ... |
Damit gilt für das regelmäßige Sechseck:
A=6(ah/2) = (6/4)sqrt(3)a² = (3/2)sqrt(3)a²
U=6a
R=a
r=h=(1/2)sqrt(3)a
d=2a
e=2h=sqrt(3)a...... |
Umkreis und Inkreis:
|
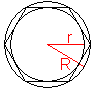
Diagonalen:
|
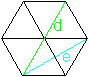
Die Größe des Innenwinkels des Sechsecks beträgt 120°.
Vom Vieleck zum Sechseck top
Das Sechseck ist der Sonderfall n=6 des Vielecks.
Kennt man die Formeln des Vielecks, so kann man die des Sechsecks berechnen.
Ist für ein
Vieleck die Seite a gegeben, so gilt
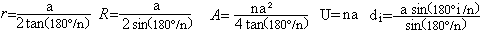
i=1,2,...n-1.
In der Rechnung treten für n=6 drei
Werte trigonometrischer Funktionen auf, nämlich tan(36°), sin(36°)
und sin(72°).
Es gilt tan(30°)=[(1/3)sqrt(3)], sin(30°)=1/2 und sin(60°)=(1/2)sqrt(3).
Damit ergibt sich
r = a/[2tan(30°)] = a/[(2/3)sqrt(3)] = (1/2)sqrt(3)a
R = a/[2sin(30°)] = a
A = 6a²/[4tan(30°)] = (6/4)sqrt(3)a² = (3/2)sqrt(3)a²
d2 = e = a sin(60°)/[sin(30°)] = [(1/2)sqrt(3)a]/(1/2)
= sqrt(3)a
d3 = d = a sin(90°)/[sin(30°)] = 2a
Eine Formel zum Sechseck top
|
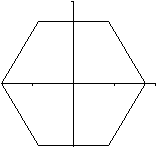
Es ist möglich, ein Sechseck in einem Koordinatensystem durch
nur
eine Gleichung zu beschreiben.
2|y|+|y-x*sqr(3)|+|y+x*sqr(3)| = 6 oder 2*abs(y)+abs(y-x*sqr(3))+abs(y+x*sqr(3))
= 6
|
Figuren im Sechseck top
Verbindet man alle Eckpunkte des Sechsecks wie in Bild 1, so
erhält man neun Diagonalen.
Es entsteht eine Reihe einfacher Figuren, wenn man nur einige Diagonalen
oder Teile von ihnen zeichnet.
2 Gleichseitiges Dreieck
3 Gleichschenkliges Trapez
4 Raute
5 Sechszackiger Stern oder Hexagramm
6 Rechteck
7 Zwei Rauten
8 Gedrehtes Sechseck im Inneren
Muster im Sechseck
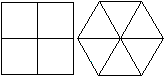
Zwei Quadrate im Sechseck
top
... ...
|
 ...
|
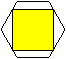
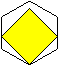
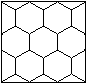
Es gibt zwei Möglichkeiten, ein möglichst großes Quadrat
in das Sechs einzupassen. Die Seitenlängen sind nach der Zeichnung
etwa gleich, so dass eine Rechnung klären muss, welche Größenbeziehung
besteht. |
1) Eine Quadratseite liegt parallel zur
Grundseite des Sechsecks.
... ... |
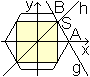Gegeben sei die Seite a des Sechsecks. Dann erhält man die Seitenlänge
des Quadrates, indem man zuerst ein Koordinatensystem einführt und
die Koordinaten des Schnittpunkts S der eingezeichneten Geraden g und h
bestimmt. Es gilt A(a|0) und B[(1/2)a|(1/2)sqrt(3)a]. Die Geradengleichung
zu AB ergibt sich über die Zwei-Punkte-Form: (y-0)/(x-a) = [(1/2)sqrt(3)a-0]/[(1/2)a-a] |
Dann ist y = [-sqrt(3)](x-a) oder y = -sqrt(3)x+sqrt(3)a.
Die Gerade h hat die Gleichung y=x.
Für den Schnittpunkt S gilt -sqrt(3)x+sqrt(3)a =x oder [(sqrt(3)+1]x=sqrt(3)a
oder x=sqrt(3)a/[(sqrt(3)+1]
oder x=(1/2)sqrt(3)[sqrt(3)-1]a oder x=(1/2)[3-sqrt(3)]a.
Die Quadratseite ist dann 2x=[3-sqrt(3)]a oder gerundet 1,27a.
2) Das Quadrat steht auf der Spitze.
... ... |
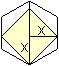Die Strecke x ist der Radius r des Inkreises, x = r = [(1/2)sqrt(3)]a.
Dann ist die Seitenlänge des Quadrats sqrt(2)x=[(1/2)sqrt(6)]a
oder gerundet 1,22a. |
Ergebnis: Das erste Quadrat ist größer als das zweite, und zwar
um 4,1%.
Fünfeck im Sechseck
... ... |
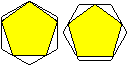Auch ein Fünfeck passt auf zweierlei Weisen in ein Sechseck.
Es sieht so aus, als sei das Fünfeck, bei dem eine Seite parallel
zu einer Sechseckseite liegt, etwas größer ist. Ein Klärung
kann eine Rechnung bringen... |
Kreis und Sechseck top
... ... |
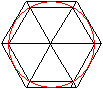Ein Kreis kann Umkreis und Inkreis zweier Sechsecke sein. Berechnet
man den Umfang der Sechsecke und bildet den Mittelwert, so erhält
eine gute Näherung des Umfangs eines Kreises.
Der Radius des Kreises sei r.
Umfang des inneren Sechsecks: 6r. Umfang des
äußeren Sechsecks: 3*sqr(5)*r.
Mittelwert: [6+3*sqrt(5)]/2 ~ ~ 2*3,15*r (Zum Vergleich
pi=3,14). Der Fehler liegt weit unter 1%. |
Das Puzzle "Wabe" top
Gegeben sind sieben sechseckige Klötze aus
Holz, deren Seiten mit Farben gekennzeichnet sind.
Man soll eine Figur wie rechts legen, wobei gleiche
Farben aneinander stoßen müssen.
(entwickelt von Torsten Sillke & Lothar Hanappel, aus der Reihe Grips
& Co, 6 Legespiele, copyright 1994)
Lösung:
...
 ...
|
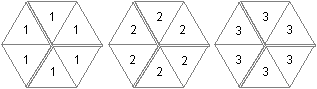
Links werden die Klötze oder Steine
noch einmal deutlicher dargestellt. |
Jedes Sechseck trägt drei Farben und zwar doppelt. Sie sind nach Rot
geordnet: Bei Stein 1 und 2 stoßen rote
Felder aneinander, bei 3, 4 und 5 liegen rote Felder einander gegenüber
und bei 6 und 7 liegt eine andere Farbe dazwischen.
Wenn man darauf vertraut, dass die Lösung symmetrisch ist, ist
anzunehmen, dass sich die Steine 1 und 2 gegenüberliegen. Dann liegt
in der Mitte Stein 4. So kommt man nach einigem Herumprobieren auf
die Lösung.
Die Farbverteilung von Stein 1 kann man mit dem Wort aabcbc kennzeichnen.
Stein 2 ist dann aacbcb zugeordnet. Insgesamt gibt es 6!/(2!*2!*2!)=90
Worte.
Puzzles dieser Art begegnet man häufig. Sie heißen im Englischen
"Matching Puzzles".
Es gibt zum Beispiel ein Puzzle mit sechs Farben bzw. mit den Zahlen
1 bis 6 an den Rändern (Buch 1, Seite 189 f.).
Sechseckzahlen top
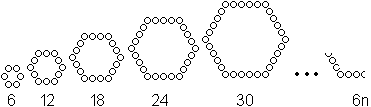
"Sechseckrand-Zahlen"
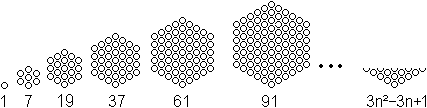
Zentrierte Sechseckzahlen ("Hex numbers")
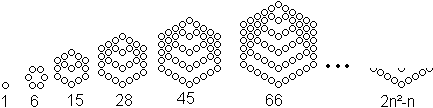
Sechseckzahlen (Jede zweite Dreieckszahl ist Sechseckzahl.)
Sechsecke in meiner Homepage
top
Hexagramm
... ... |
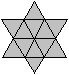Setzt man auf die Seiten eines Sechsecks gleichseitige Dreiecke, so
entsteht ein sechszackiger Stern,
das Hexagramm. |
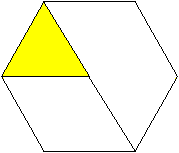
Trihexaflexagon
Man kann Papierstreifen zu Sechsecken mit Einsen vorne und Zweien hinten
falten. Klappt man die "Flexagons" in der Mitte auf, entsteht ein neues
Sechseck 3, das vorher unsichtbar war.
Mehr findet man auf meinen Seiten Flexagons
und Hexahexaflexagons.
Sechsecke aus Kreisbögen
Mehr findet man auf meiner Seite Kreisteile.
Ein Sechseck aus Kreisen
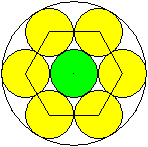
Man kann um einen Kreis sechs weitere Kreise mit gleichen Radien so
legen, deren Mittelpunkte ein Sechseck bilden.
Mehr findet man auf meiner Seite Kreise im
Kreis.
Parkettierung mit Sechsecken
|
Hauswand am Hafen von Chania auf Kreta
|
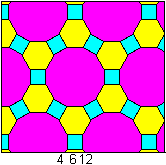
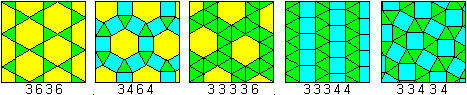
Homogene Parkettierungen
Mehr findet man auf meinen Seiten Parkettierungen
und Gleichseitiges Dreieck.
Sechsecke und Würfel
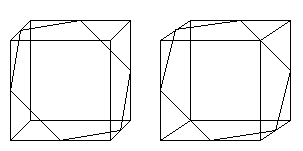
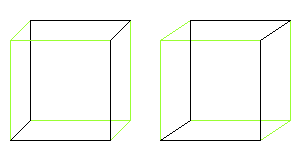Mehr findet man auf meinen Seiten Stereogramm
und Würfel.
Polyiamonds
Polyiamonds sind Figuren, die man aus gleichseitigen
Dreiecken bildet. Aus Hexiamonds z.B. kann man Sechsecke legen.
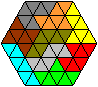Mehr findet man auf meiner Seite Polyiamonds.
Polywaben
Polywaben sind Figuren, die man aus Sechsecken bilden kann. Bekannt
sind die sieben Tetrawaben.
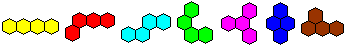Sie bilden die Spielsteine für ein Puzzle.
Mehr findet man auf meiner Seite Polywaben.
In der Linkliste findet man Spiele, die Sechsecke benutzen.
Magisches Sechseck
... ... |
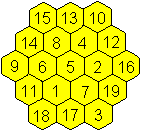Das magisches Sechseck ist eine Figur, die die Zahlen 1 bis 19 enthält
und bei der die 15 Summen horizontal (-), schräg nach oben rechts
(/) und schräg nach oben links (\) gleich sind, nämlich 38.
Mehr findet man auf meiner Seite Magisches
Sechseck. |
Sechseck und Körper
Es gibt Körper, die u.a. von Sechsecken
begrenzt werden.
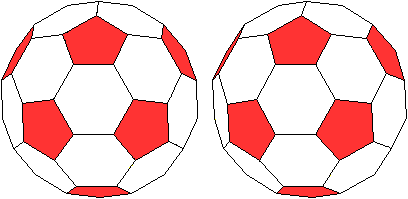
Abgestumpftes Ikosaeder - 20 Sechsecke
Die Bildpaare erlauben eine dreidimensionale Ansicht der Körper.
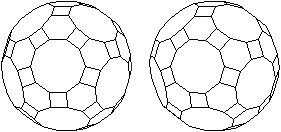
Großes Rhombenikosidodekaeder
- 20 Sechsecke
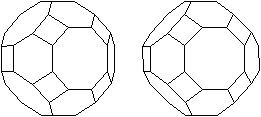
Großes Rhombenkuboktaeder
- acht Sechsecke
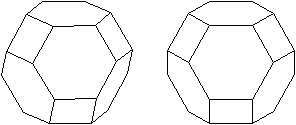
Abgestumpftes Oktaeder - acht
Sechsecke
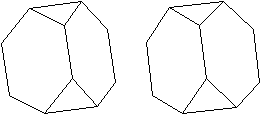
Abgestumpftes Tetraeder - vier Sechsecke
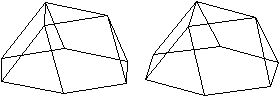
Dreieckskuppel - ein Sechseck
Ferner
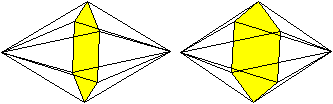
Bipyramide - ein Sechseck
Bestimmte Körper zeigen bei bestimmten
Ansichten Sechsecke.
"Design at Pompeii"
|
|
Sechsecke im Internet top
Deutsch
Wikipedia
Sechseck, Hexagramm
www.sachsentext.de
Hexogonal,
Wabenrätsel,
Takumi
Englisch
David King
Hall of Hexagons
Eric W. Weisstein (World of Mathematics)
Hexagon, Cosine
Hexagon, Figurate
Number, Hex Number,
Talisman
Hexagon,
Magic
Hexagon,
Hexagram
Graham's
Biggest Little Hexagon
Jaap Scherphuis
Tantrix
John Baker (Natural Maths)
Hexagonia
Lou Hoelbling
The World's Largest Six
Ring Magical Hexagon?
Patricia L. Cummings
How
to Make a Hexagon Quilt
Torsten Sillke
Magic
Hexagon
Wikipedia
Hexagon, Hexagram,
Magic
hexagon, Hexagonal
tiling
Referenzen top
(1) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont taschenbuch1480)
[ISBN 3-7701-2097-3]
(2) Martin Gardner: Mathematischer Karneval, Frankfurt a.M 1975 [ISBN
3 550 07675 4]
(3) Martin Gardner: Mathematisches Labyrinth, Braunschweig/Wiesbaden
1979 [ISBN 3-528-08402-2]
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage
http://www.mathematische-basteleien.de/
©
2004 (ergänzt 2010) Jürgen Köller
top |
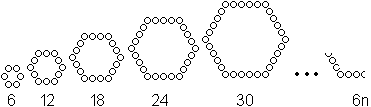
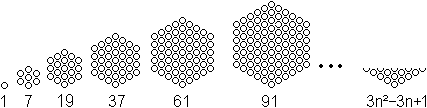
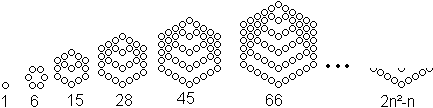
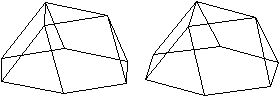
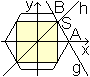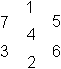
