|
Was ist ein abgestumpftes Ikosaeder?
... ... ...
|
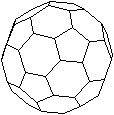
Ein abgestumpftes Ikosaeder ist ein Körper, der
von 12 regelmäßigen Fünfecken und 20 regelmäßigen
Sechsecken gebildet wird. |
Neben den 12+20=32 Seitenflächen hat das abgestumpfte
Ikosaeder 90 Kanten und 60 Eckpunkte.
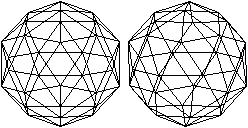
Wer den 3D-Blick beherrscht,
sieht das abgestumpftes Ikosaeder räumlich.
durchsichtig
|
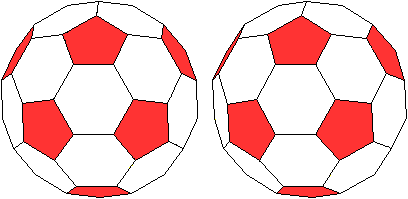
undurchsichtig
|
Entstehung
...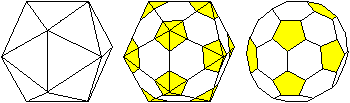 ... ... |
Er entsteht aus einem Ikosaeder, indem man die Ecken
passend abschneidet. Dazu teilt man die Kante in drei gleiche Teile.
An den Ecken des Ikosaeders entstehen Fünfecke.
Die Seitenflächen des Ikosaeders reduzieren sich auf Sechsecke. |
Einordnung
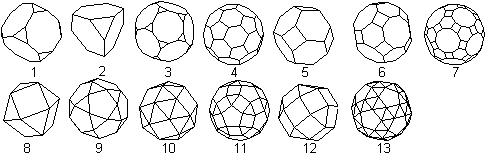 Da beim abgestumpften Ikosaeder (4) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört es zu den 13
archimedischen
Körpern.
Da beim abgestumpften Ikosaeder (4) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört es zu den 13
archimedischen
Körpern.
Beschreibungen top
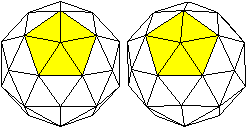
Lage der Fünf- und Sechsecke
...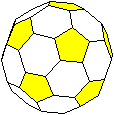 |
Jedes Fünfeck ist isoliert........................... |
...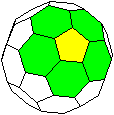 |
Jeweils fünf Sechsecke bilden einen Ring. |
...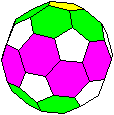 ... ... |
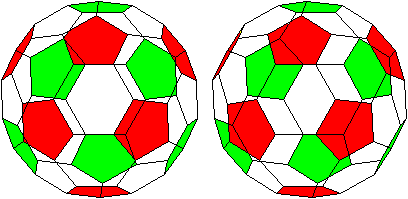
Zehn Sechsecke laufen "am Äquator" als Zickzacklinie
um den Körper herum.
Die beiden Ringe in "Polnähe" sind gegeneinander
gedreht. |
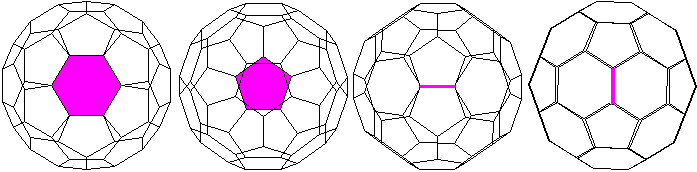
Parallelprojektionen
Ein Sechseck, ein Fünfeck, eine Kante, eine Kante und
ein Eckpunkt liegen vorne.
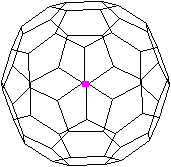
Schlegel-Diagramm
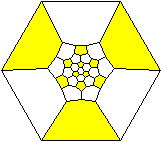
Diagonalen
240 Flächendiagonalen
...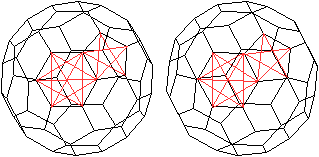 .... .... |
Die Diagonalen der Fünf- und Sechsecke bilden die
Flächendiagonalen des abgestumpften Ikosaeders. Jedes Fünfeck
hat 5 Diagonalen. Jedes Sechseck hat 9 Diagonalen.
Das führt zu insgesamt 12*5+20*9=240 Flächendiagonalen. |
1440
Raumdiagonalen
...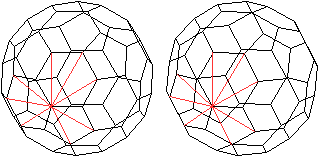 ... ... |
Von jedem der 60 Eckpunkte gehen Verbindungslinien zu
den anderen Eckpunkten aus. Das sind 8 Flächendiagonalen und 3 Kanten,
wie die Zeichnung zeigt. In 60-11=49 Punkten enden dann Raumdiagonalen.
Das führt zu insgesamt (1/2)*60*48=1440 Raumdiagonalen
des abgestumpften Ikosaeders. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das abgestumpfte Ikosaeder bedeutet das, dass
es (1/2)*59*60=1770 Verbindungslinien gibt.
Das sind die 90 Kanten, 240 Flächendiagonalen und
1440 Raumdiagonalen.
Bau des Körpers
top
Die Schönheit dieses Körpers erschließt
sich eigentlich erst, wenn man ihn bastelt.
... ... ... |
Es ist sicherlich viel Arbeit, das abgestumpfte Ikosaeder
aus einem Netz zu basteln.
G. Korthals Altes bietet eine Vorlage an (URL unten). |
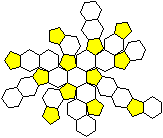
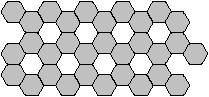
Viel schneller und origineller
entsteht der Körper allein mit Hilfe regelmäßiger Sechsecke.
Die Fünfecke erscheinen beim fertigen Körper
als Löcher.
Die Bastelvorlage enthält 31 Sechsecke. Für den
Körper braucht man aber nur 20. Elf Sechsecke kleben aufeinander.
- Vielleicht ist es sicherer, vor dem Kleben Büroklammern zu verwenden,
wie ich es getan habe. Der Link auf die Vorlage existiert nicht mehr, hier
ist ein Ersatz.
Wer sich in der Flechttechnik
auskennt, findet eine Vorlage bei H.B.Meyer (URL unten).
Größen top
Das abgestumpfte Ikosaeder sei durch die Kantenlänge
a gegeben.
Daraus lassen sich die weiteren Größen Radius
R
der Umkugel, Volumen
V, Oberfläche O, Abstand d5
gegenüberliegender Fünfecke, Abstand d6 gegenüberliegender
Sechsecke berechnen.
Es gilt
Herleitung
Vorweg: Es werden hier Formeln verwendet, die an anderen
Stellen meiner Homepage hergeleitet werden.
Regelmäßiges
Fünfeck
Flächeninhalt:
A5 = (1/4)sqrt[25+10sqrt(5)]a²
Umkreises des Fünfecks:
R5 = (1/10)sqrt[50+10*sqrt(5)]a |
Regelmäßiges
Sechseck
Flächeninhalt:
A6 = (3/2)sqrt(3)a²
.
. |
Ikosaeder
Abstand paralleler Gegenseiten:
d = (1/2)[1+sqrt(5)]a'
.
. |
Wie gesagt entsteht das abgestumpfte Ikosaeder
aus dem Ikosaeder. Für die Rechnungen ist es hilfreich, beim
Ikosaeder durch eine Kante und den Mittelpunkt eine Schnittfläche
zu legen.
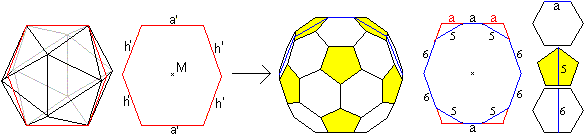 Überträgt man diesen Schnitt auf das abgestumpfte
Ikosaeder, so ergibt sich das blaue Zehneck aus zwei Kanten und je vier
Höhen von Fünf- und Sechsecken.
Überträgt man diesen Schnitt auf das abgestumpfte
Ikosaeder, so ergibt sich das blaue Zehneck aus zwei Kanten und je vier
Höhen von Fünf- und Sechsecken.
Die Mittelpunkte des Ikosaeders und des abgestumpften
Ikosaeders fallen zusammen.
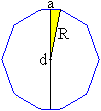
Radius
der Umkugel
d = (1/2)[1+sqrt(5)]a' ist beim Ikosaeder (und auch hier)
der Abstand paralleler Gegenseiten.
Es gilt a' = 3a und somit d = (3/2)[1+sqrt(5)]a.
... ... ...
|
Nach dem Satz des Pythagoras ist R² = (d/2)²+(a/2)².
Daraus folgt R = (1/4)sqrt[58+18sqrt(5]a. |
...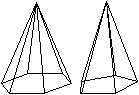 ... ... |
Verbindet man die Eckpunkte der Fünf- und Sechsecke
mit dem Mittelpunkt des Körpers, so entstehen gerade regelmäßige
Pyramiden.
Alle Seitenlinien der Pyramiden sind so lang wie der Radius
der Umkugel. |
Oberfläche
Die Oberfläche wird von Fünfecken
und Sechsecken gebildet.
Das Fünfeck hat den Flächeninhalt A5 =
(1/4)sqrt[25+10sqrt(5)]a², das Sechseck A6 = (3/2)sqrt(3)a².
Es ergibt sich O = 12A5 +20A6 =
3{sqrt[25+10sqrt(5)]a²+10sqrt(3)}a².
Abstand
gegenüberliegender Fünfecke
Zunächst wird die Höhe der Fünfeckpyramide
bestimmt.
...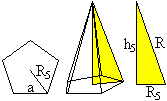 ... ... |
Sie ist nach dem Satz des Pythagoras h5 =
sqrt(R²-R5²).
Dabei ist R5 = (1/10)sqrt[50+10*sqrt(5)]a
der Radius des Umkreises des Fünfecks. |
Mit R = (1/4)sqrt[58+18sqrt(5)]a erhält man h5
=
sqrt{(1/40)[125+41sqrt(5)]}a.
Dann ist d5 = 2h5 = sqrt{(1/10)[125+41sqrt(5)]}a.
Abstand
gegenüberliegender Sechsecke
Zunächst wird die Höhe der Sechseckpyramide
bestimmt.
...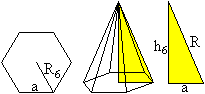 ... ... |
Sie ist nach dem Satz des Pythagoras h6 =
sqrt(R²-a²). Dabei ist R6 = a der Radius des Umkreises
des Sechsecks.
Mit R = (1/4)sqrt[58+18sqrt(5)]a erhält man h6
=
sqrt{(1/8)[21+9sqrt(5)]}a.
Dann ist d6 = 2h6 = sqrt{(1/2)[21+9sqrt(5)]}*a. |
Volumen
Das Volumen setzt sich aus den Volumina der Fünf-
und Sechseckpyramiden zusammen:
V = 12*(1/3)A5h5+20*(1/3)A6h6
(#).
Die Höhen sind h5 = sqrt[(1/40)125+41sqrt(5)]*a
und h6 = sqrt{(1/8)[21+9sqrt(5)}a
und die Grundflächen A5 = (1/4)sqrt[25+10sqrt(5)]a²
und A6 = (3/2)sqrt(3)a².
Setzt man diese Terme in die Gleichung (#) ein, so ergibt
sich nach längerer Rechnung
V = sqrt{(1/8)[1035+455sqrt(5)]}a³+sqrt{(1/4)[3150+1350sqrt(5)]}a³.
Das Programm Derive von etwa 1990 (noch mit Tastenbedienung)
hilft, den Term zu vereinfachen:
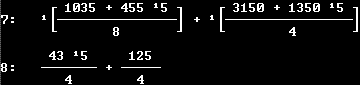 Ergebnis: V = (1/4)[125+43sqrt(5)]a³
Ergebnis: V = (1/4)[125+43sqrt(5)]a³
Inkugel
Das abgestumpfte Ikosaeder hat keine Inkugel. Sein Mittelpunkt
ist vom Fünfeck weiter entfernt als vom Sechseck:
Es gilt gerundet h5 = 2,33a und h6 =
2.27a. Im Vergleich dazu ist der Radius der Umkugel R = 2,47a.
Eine Kugel mit dem gleichen Volumen wie das abgestumpfte
Ikosaeder hat einen Radius von 2,36a.
Der duale Körper
top
Verbindet man die Mittelpunkte der nebeneinanderliegenden
Fünf- und Sechsecke, die das abgestumpfte Ikosaeder bilden, so entsteht
der duale Körper.
Wenn das abgestumpfte Ikosaeder 60 Kanten, 32 Flächen
und 90 Ecken hat, dann hat der duale Körper 60 Kanten, 90 Flächen
und 32 Eckpunkte. Die Anzahl der Flächen und Ecken tauschen sich aus.
Der duale Körper wird von Dreiecken begrenzt. Fünf
Dreiecke bilden jeweils eine Fünfeckpyramide.
Der Körper heißt Pentakisdodekaeder.
Fußball und
Buckyball top
Das abgestumpfte Ikosaeder hat Berühmtheit erlangt,
weil einmal eine Spielart des Balles des Fußballspiels bis auf die
Wölbung, die durch den Innendruck entsteht, diese Form hat. Zum anderen
gibt es Makromoleküle aus Kohlenstoffatomen in der gleichen Form.
Dieses Molekül heißt das Fulleren (Mehrzahl: die Fullerene)
oder der Buckyball.
Weitere Informationen erhält man über die Links
im nächsten Kapitel.
Abgestumpftes
Ikosaeder im Internet top
Deutsch
Friedrich Cordes
Fußball
- Ikosaeder
H.B.Meyer
Abgestumpftes
Ikosaeder
Raúl Rojas
Brazuca:
das Eckige im Runden
Thomas Burmester
Himmelskugel
(aus Holz)
Werner Brefeld
Fußball,
Platonische Körper und Archimedische Körper
Wikipedia
Abgestumpftes
Ikosaeder, Fulleren,
Ikosaeder,
Archimedischer
Körper, Fußball
(Sportgerät), Pentakisdodekaeder
Englisch
Eric W. Weisstein (MathWorld)
Truncated
Icosahedron, Pentakis
Dodecahedron, Truncation,
Archimedean
Solid, Dual
Polyhedron
Geneviève Tulloue ( Figures Animées pour
la Physique )
Polyhedra
(Applets)
G. Korthals Altes
Paper
Model Truncated Icosahedron (soccer ball)
H.B.Meyer
Truncated
Icosahedron
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Wikipedia
Truncated
icosahedron, Fullerene,
Icosahedron,
Football
(ball), Pentakis
dodecahedron
Französisch
Robert FERRÉOL
ICOSIDODÉCAÈDRE
TRONQUÉ
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2006, überarbeitet 2013, Jürgen Köller
top |



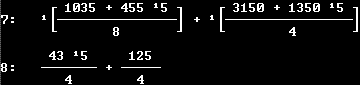
 ...
...

 ...
...

 ...
...
 ....
.... ...
... ...
...

 ...
... ...
...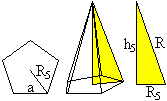 ...
...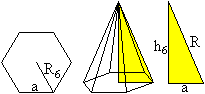 ...
...