|
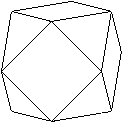
Was ist ein Kuboktaeder?
... ... ...
|
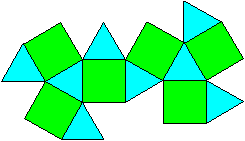
Ein Kuboktaeder ist ein Körper, der von sechs Quadraten
und acht gleichseitigen Dreiecken gebildet wird. |
Neben den 6+8=14 Seitenflächen hat das Kuboktaeder
24 Kanten und 12 Eckpunkte.
Wer den 3D-Blick beherrscht,
sieht das Kuboktaeder räumlich.
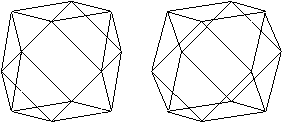
durchsichtig
|
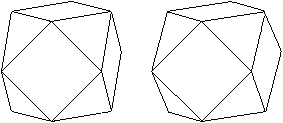
undurchsichtig
|
Entstehung
Das Kuboktaeder kann aus einem Würfel entstehen.
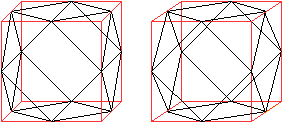
Man verbindet die Kantenmitten des Würfels. Dadurch
entstehen an den Würfelecken acht Pyramiden, die man entfernt. Der
Restkörper ist dann das Kuboktaeder.
Name
Offenbar setzt sich das Wort Kuboktaeder aus Kubus und
Oktaeder zusammen.
... ... ...
|
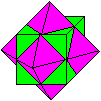
Setzt man nämlich auf die Würfelflächen
quadratische Pyramiden wie links im Bild, so kann man sich vorstellen,
dass sich ein (grüner) Würfel und ein (rotes) Oktaeder durchdringen.
Der gemeinsame Bereich, der Kern, ist das Kuboktaeder. |
Andere Namen sind Mittelkristall oder Kubooktaeder.
Einordnung
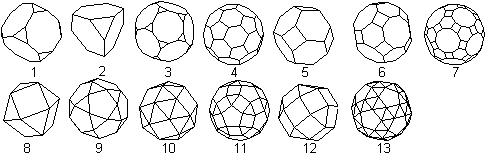 Da beim Kuboktaeder (8) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört er zu den 13
archimedischen
Körpern.
Da beim Kuboktaeder (8) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört er zu den 13
archimedischen
Körpern.
Beschreibungen
top
Umgebungen
|
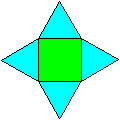
Jedes Quadrat wird von 4 gleichseitigen Dreiecken umgeben. |
|
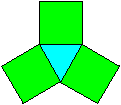
Jedes gleichseitige Dreieck wird von 3 Quadraten umgeben. |
Parallelprojektionen
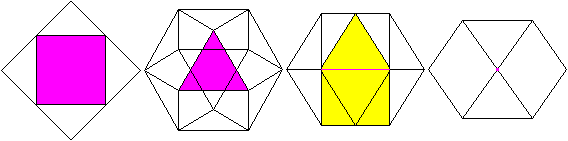
Ein Quadrat, ein Dreieck, eine Kante und ein Eckpunkt
liegen vorne.
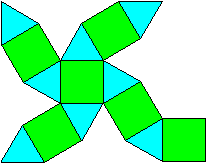
Netze
Schlegel-Diagramm
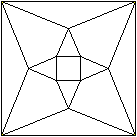
Diagonalen
12 Flächendiagonalen
...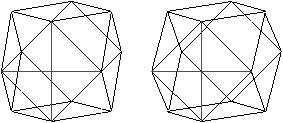 .... .... |
Die Diagonalen der Quadrate bilden die Flächendiagonalen
des Kuboktaeders. Jedes Quadrat hat 2 Diagonalen.
Das führt zu insgesamt 6*2=12 Flächendiagonalen. |
30
Raumdiagonalen
...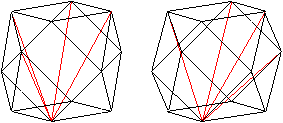 ... ... |
Von jedem der 12 Eckpunkte gehen je 5 Raumdiagonalen
aus.
Das führt zu insgesamt (1/2)*12*5=30 Raumdiagonalen
des abgestumpften Würfels. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das Kuboktaeder bedeutet das, dass es (1/2)*11*12=66
Verbindungslinien gibt.
Das sind die 24 Kanten, 12 Flächendiagonalen und
30 Raumdiagonalen.
Größen top
Das Kuboktaeder
sei durch die Kantenlänge a gegeben.
Daraus lassen sich weiteren die
Größen Radius R der Umkugel, Radius rk der Kantenkugel,
Volumen V, Oberfläche O, Abstand der Dreiecke d3 und Abstand
der Quadrate d4 berechnen.
Es gilt:
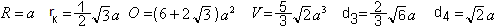
Herleitung
der Formeln
Umkugel
|
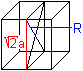
Es wird nur der erzeugende Würfel dargestellt.
In der Zeichnung kann man R=a ablesen. |
Kennt man die Sechsecke im Kuboktaeder, so ist R=a noch einfacher
einzusehen (siehe unten).
Kantenkugel
Bei archimedischen Körpern liegen die Kantenmitten
auf einer Kugel, der Kantenkugel.
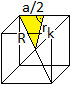 |
Es wird nur der erzeugende Würfel betrachtet.
Der Radius rk der Kantenkugel kann über
den Radius R der Umkugel bestimmt werden.
Im rechtwinkligen Dreieck gilt rk² =
R²-[(1/2)a]² = a²-(1/4)a² = (3/4)a². Dann ist
rk=(1/2)sqrt(3)a. |
Oberfläche
Ist a die Kantenlänge, so ist die Oberfläche
O = 6*a²+8*(1/4)sqrt(3)a² = [6+2sqrt(3)]a².
Es wird die Flächenformel A = (1/4)sqrt(3)a²
eines gleichseitigen Dreiecks benutzt.
Volumen
Vorweg: Der erzeugende Würfel hat die Kantenlänge
sqrt(2)a. Sein Volumen V' = 2sqrt(2)a³.
Es bietet sich der Weg an: Das Volumen des erzeugenden
Würfels wird um die Volumen der acht abgeschnittenen Dreieckspyramiden
vermindert.
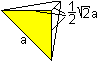
|
Für das Volumen einer abzuschneidenden Pyramide
gilt:
V'' = (1/3)*[(1/2)sqrt(2)a]²*[(1/2)sqrt(2)a] = ...
=
(1/24)sqrt(2)a³. |
Das Volumen des Kuboktaeder ist dann V = V'-8V'' = 2sqrt(2)a³-8*[(1/24)sqrt(2)a³]
= (5/3)sqrt(2)a³.
Abstand
der Dreiecke
Beim Kuboktaeder liegen sich zwei Dreiecksflächen
gegenüber. Ihr Abstand d2 ist gleich der Raumdiagonalen
des Würfels sqrt(6)a, vermindert um die doppelte Höhe der Eckenpyramide.
Es gilt V'' = (1/3)[(1/4)sqrt(3)a²]h. Dabei ist
die Grundfläche das gleichseitige Dreieck.
Andererseits ist V'' = (1/24)sqrt(2)a³ (s.o)
Daraus folgt h = (1/6)sqrt(6)a.
Der gesuchte Abstand ist d2 = sqrt(6)a-2[sqrt(6)/6]a
= (2/3)sqrt(6)a, wzbw.
Abstand
der Quadrate
Beim Kuboktaeder liegen sich zwei Quadratflächen
gegenüber. Ihr Abstand ist d1=sqrt(2)a.
Winkel zwischen zwei
Seitenflächen
Der Winkel zwischen Dreieck und Quadrat beträgt
125°16'.
Quelle (2)
Verschiedenes top
Sechsecke
Beim Kuboktaeder liegen
immer zwei Dreiecke paarweise gegenüber. Genau in der Mittelebene
liegt ein regelmäßiges Sechseck als Begrenzungslinie.
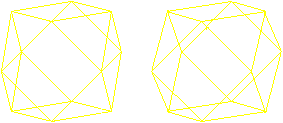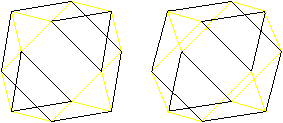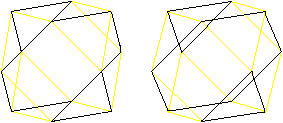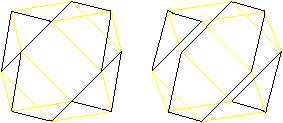
Es gibt vier verschiedene Sechsecke.
Oktaeder
bauen
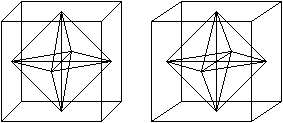
Man kann die acht vom erzeugenden Würfel abgeschnittenen
Dreieckspyramiden zu einem Oktaeder zusammensetzen, der in den erzeugenden
Würfel passt.
Dichteste
Kugelpackung
Legt man an eine (rote) Kugel in
der Ebene sechs gleiche Kugeln und in die Vertiefungen oben und unten je
drei weitere Kugeln, so bilden die Mittelpunkte der (grauen) Kugeln die
Eckpunkte eines Kuboktaeders.
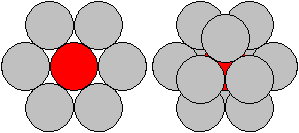
Das führt zur kubisch dichtesten Kugelpackung im Raum.
12 Kugeln berühren eine Zentralkugel.
Im zweidimensionalen Fall berühren 6 Kreise eine
Zentralkreis, im vierdimensionalen 24 Hyperkugeln eine Zentralhyperkugel.
Eine Zahl wie 6,12 oder 24 heißt "kissing number".
Eulerscher
Weg
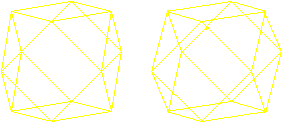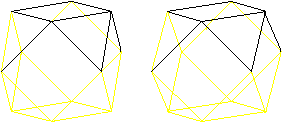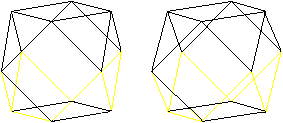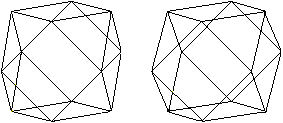
Beim Kuboktaeder treffen an jeder Ecke vier Kanten aufeinander.
Deshalb ist es möglich, den Kanten so zu folgen, dass man jede Kante
genau einmal passiert.
Mehr findet man auf meiner Seite Haus
des Nikolaus.
Papiermodell
Zum Buch "M.C.Escher Kaleidozyklen" gehört auch
die Vorlage für einen Kuboktaeder.

Weitere Körper
top
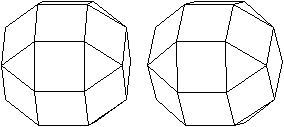
Zwei Hemipolyeder
...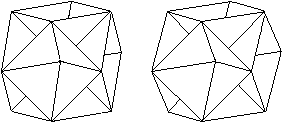 ... ... |
Verbindet man die Eckpunkte des Kuboktaeders mit dem
Mittelpunkt, so entstehen Vertiefungen in Form von quadratischen und dreiseitigen
Pyramiden. Man könnte das Gebilde auch aus den vier Sechsecken im
Kuboktaeder erzeugen. |
Oktahemioktaeder
...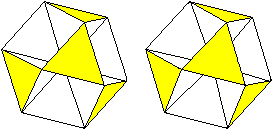 ... ... |
Füllt man nur die dreiseitigen
Pyramiden aus, so entsteht ein Körper aus acht dreiseitigen Pyramiden,
die sich berühren und deren Spitzen sich im Mittelpunkt treffen. |
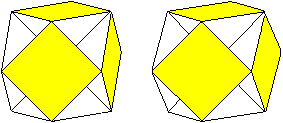
Kubohemioktaeder
... ... ...
|
Füllt man nur die quadratischen
Pyramiden aus, so entsteht ein Körper aus sechs quadratischen Pyramiden,
die sich berühren und deren Spitzen sich im Mittelpunkt treffen. |
Rhombendodekaeder
...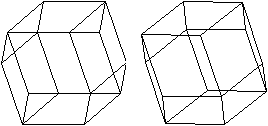 ... ... |
Verbindet man die Mittelpunkte benachbarter Seitenflächen
des Kuboktaeders, so entsteht sein dualer Körper, das Rhombendodekaeder. |
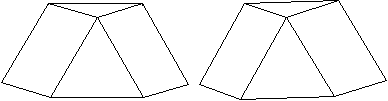
Dreieckskuppel
(Triangular Cupola)
Die Dreieckskuppel entsteht, wenn
man das Kuboktaeder längs eines Sechsecks halbiert.
Sie wird von einem Sechseck, drei Quadraten und vier
gleichseitigen Körpern gebildet.
Sie ist der Johnson-Körper J3.
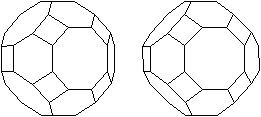
Rhombenkuboktaeder
Rainbow Cube
top
...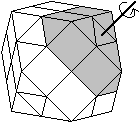 ... ... |
Das Kuboktaeder ist zu einem Puzzle geworden. Es stammt
aus Japan.
Zwischen der Sechseckebene und dem Außendreieck
wird eine Mittelebene gelegt. So entsteht zu jedem Dreieck eine Scheibe,
die drehbar ist, und zwar um eine Achse, die senkrecht zur Dreiecksebene
liegt und durch den Körpermittelpunkt verläuft.
Links ist eine von acht drehbaren Scheiben grau gekennzeichnet. |
... ... ... |
Die Außenflächen des Kuboktaeder sind wie
bei Rubiks Zauberwürfel gefärbt. Gegenüberliegende
Flächen haben die gleiche Farbe.
Dreht man planlos einige der acht Schichten, so wird der
Körper bunt. Aufgabe ist es den Körper so zu ordnen, dass die
Außenflächen wieder einfarbig werden. |
So sieht das Puzzle aus:

Kuboktaeder im
Internet top
Deutsch
Claus Michael Ringel
Kuboktaeder
Geneviève Tulloue ( Figures Animées pour
la Physique )
Polyhedra
(Applets)
H. B. Meyer (Polyeder aus Flechtstreifen)
Kubo-Oktaeder
Wikipedia
Kuboktaeder,
Archimedischer
Körper, Großes
Rhombenkuboktaeder, Rhombendodekaeder
Englisch
Eric W. Weisstein (MathWorld)
Cuboctahedron,
Triangular
Cupola, Archimedean
Solid, Kissing
Number, Octahemioctahedron,
Cubohemioctahedron,
George W. Hart
Virtual
Polyhedra (The Encyclopedia of Polyhedra)
Gijs Korthals Altes
Paper
model Cuboctahedron
H. B. Meyer (Polyhedra plaited with paper strips)
Cuboctahedron
Jaap Scherphuis
Rainbow
Cube
Kenneth James Michael MacLean
THE
CUBEOCTAHEDRON
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programms.
Wikipedia
Cuboctahedron,
Truncated
cuboctahedron, Triangular
cupola, Rhombic
dodecahedron, Hemipolyhedron,
Cubohemioctahedron,
Octahemioctahedron
Französisch
Robert FERRÉOL
CUBOCTAÈDRE
Referenzen
top
(1) Doris Schattenschneider und Wallace Walker, M.C.Escher
Kaleidozyklen, Köln 1992
(2) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961 (Seite 102)
Feedback: Emailadresse
auf meiner Hauptseite
Diese Seite ist auch in Englisch
vorhanden.
URL meiner Homepage: https://www.mathematische-basteleien.de/
© 2004,
überarbeitet 2013, Jürgen Köller
top |






 ...
...


 ...
...

 ....
.... ...
...





 ...
... ...
... ...
... ...
...

 ...
... ...
...