|
Was sind Kreise im Kreis?
... ... ... |
Das sind Kreise, die sich berühren, in einem Umkreis
liegen und ihn von innen berühren.
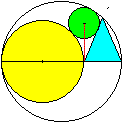
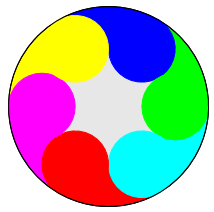
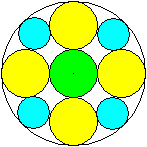
Links ist ein Beispiel. Ist R der Radius des ganzen Kreises,
r der Radius der gelben Kreises, x des blauen und y der grünen Kreise,
so gilt hier r=R/2, x=R/3 und y=R/4. |
Martin Gardner (1) stellt fest, dass
es Hunderte von Figuren dieser Art gibt, die den Weg in die Unterhaltungsmathematik
gefunden haben. Schon deshalb findet man auf dieser Seite nur eine kleine,
persönliche Auswahl.
Ketten aus Kreisen
top
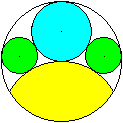
Die folgenden fünf Figuren bestehen aus einer Kette
von (gelben) Kreisen um einen (grünen) Zentralkreis und an den Rändern
aus (blauen) Lückenkreisen.
In den Formeln ist
R der Radius des Umkreises
r der Radius der (gelben) Kreise. Diese Kreise bilden
die Kette.
x der Radius der (blauen) Lückenkreise
y der Radius des (grünen) Zentralkreises.
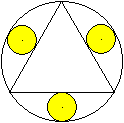
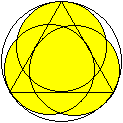
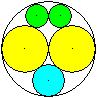
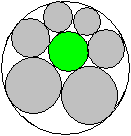
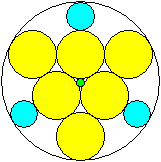
Drei gleiche Kreise im Kreis
r=[2*sqrt(3)-3]*R x=[2*sqrt(3)-1]/11*R
y=[7-4*sqrt(3)]*R
Herleitungen
...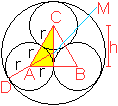 |
Man verbindet die Mittelpunkte der Kreise und erhält
das gleichseitige Dreieck ABC.
Für die Höhe h gilt nach dem Satz des Pythagoras
h²=(2r)²-r²=3r² oder h=sqrt(3)r.
Es gilt für den gegebenen Radius DM=R=r+(2/3)h=r+(2/3)sqrt(3)r.
Dann ist r=R/[1+(2/3)sqrt(3)]=3R/[3+2sqrt(3)]=[2*sqrt(3)-3]*R,
wzbw.. |
...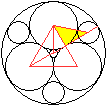 |
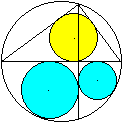
Im gelben Dreieck gilt nach dem Satz des Pythagoras (r+x)²=r²+[R-(1/3)h-x]².
Daraus ergibt sich nach längerer Rechnung x=[2*sqrt(3)-1]/11*R. |
...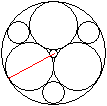 |
Es gilt R=2r+y.
Daraus folgt y=R-2r=R-2[2*sqrt(3)-3]R=[7-4*sqrt(3)]R. |
Formeln für
die Ketten top
Gibt man beliebige gleiche Kreise
vor, so werden sie in seltenen Fällen eine geschlossene Kette um einen
Zentralkreis bilden.
Unter welchen Bedingungen ist die
Kette geschlossen?
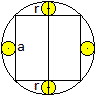
Nach der Zeichnung ist die Kreiskette aus n Kreisen geschlossen,
wenn n*alpha=360° oder alpha/2=180°/n ist.
...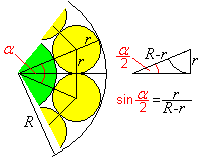 ... ... |
Nach der nebenstehenden Formel sin(alpha/2)=r/(R-r) ist
r:R=sin (180°/n)/[1+sin(180°/n].
Ergebnis: Zu jeder Kreisanzahl n gibt es ein Verhältnis
der Radien r:R.
Daraus folgt weiter:
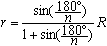 Für den Zentralkreis ergibt sich y=R-2r.
Für den Zentralkreis ergibt sich y=R-2r. |
In die Lücken zwischen dem Umkreis
und den gelben Kreisen kann man (blaue) gleiche Kreise mit dem Radius x
legen.
...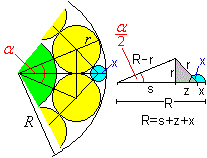 |
Es gilt (r+x)^2 = r^2+z^2, wobei z = R-x-z und
s = (R-r)cos(180°-n) ist.
Dann ist (r+x)^2 = r^2+[R-(R-r)cos(180°-n)-x]^2.
Für x ergibt sich daraus:
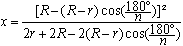
|
Anwendung der Formeln
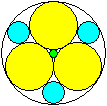
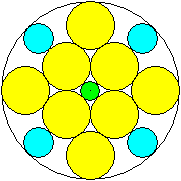
Vier gleiche Kreise im Kreis
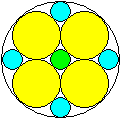
r=[sqrt(2)-1]*R x=(1/7)[2*sqrt(2)-1]*R
y=[3-2*sqrt(2)]*R
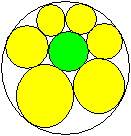
Fünf gleiche Kreise im
Kreis
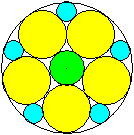
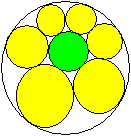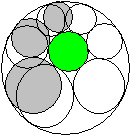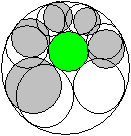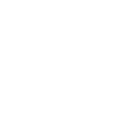
Sechs gleiche
Kreise im Kreis
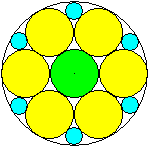
r=R/3 x=(1/39)[15-6*sqrt(3)]*R
y=R/3
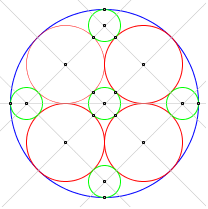
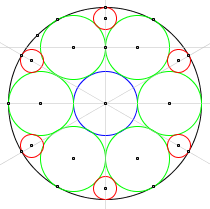
Acht gleiche Kreise im Kreis
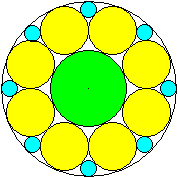
Kombination
zweier Ketten
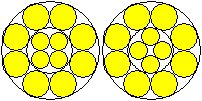
|
|
Paul Kraincuk überprüfte die Formeln für
n=3, n=4 und n=6 mit Geogebra
und fand einen Fehler. Danke. |
Steiner-Ketten top
Wenn der Zentralkreis nicht konzentrisch zum Umkreis
liegt, gibt es manchmal auch geschlossene Ketten. Diese Ketten hat im 19.
Jahrhundert der Schweizer Mathematiker Jakob Steiner untersucht.
Steiner fand heraus:
Falls wie links eine geschlossene Kette existiert, so
gibt es zu jedem passenden (grauen) Anfangskreis eine neue Kette.
Pappus-Kette top
...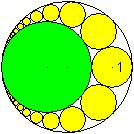 ... ... |
Berührt der grüne Zentralkreis den Umkreis
von innen, so gibt es zunächst einmal den Kreis 1 rechts, so dass
die Mittelpunkte horizontal liegen.
Zu diesem gelben Kreis 1 gibt es oben und unten immer
kleiner werdende Kreise, die zusammen die Pappus-Kette bilden. |
... ... ... |
In der Pappus-Kette steckt die bekannte Figur "Arbelos".
Kreise der Pappus-Kette sind dann Inkreise.
 |
Programm
zum Erstellen von Kreisketten top
Dr. Volker Pöhls sandte mir ein Programm zum Erstellen
von Kreisketten mit den folgenden Parametern.
(Radius des Umkreises, Anzahl der Kreise einer Kette,
Anzahhl der Ringe)
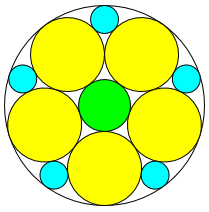
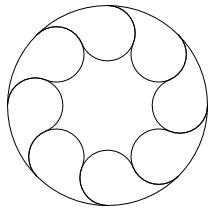
(100,5,1)
|
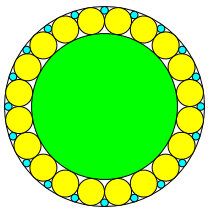
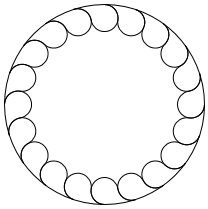
(100,20,1)
|

(100,50,1)
|
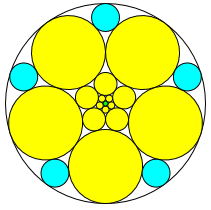
(100,5,3)
|
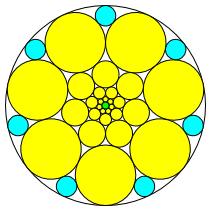
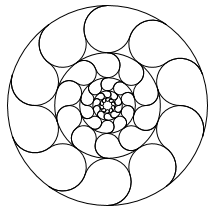
(100,7,4)
|
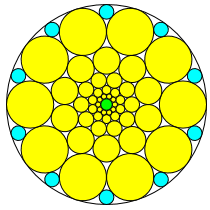
(100,10,5)
|
Wer das Programm ausprobieren
möchte, der ruft den Logo Interpreter mit https://www.calormen.com/jslogo/
auf. Das Programm kann man in jslogo kostenlos und ohne Anmeldung laufen
lassen. - Der Quellcode steht hier. Er
wird unten in den Logo Interpreter eingelesen. In die letzte Zeile schreibt
man z.B. für die Zeichnung unten links kreise.en.eck4 100 5 3.
Eine Abänderung des
Programms erzeugt "Fischblasen".
Weitere Kreise
im Kreis (Entwürfe) top
Wie groß sind die Radien der
inneren Kreise, wenn der Radius des Umkreises gegeben ist?
Spielereien mit
Münzen
top
... ... ... |
So ein Zufall:
Die acht verschiedenen Euromünzen bilden eine geschlossene
Kette mit Zentralkreis
(fast).
 |
Diese Kuriosität habe ich auf einer Seite von Hans Melissen
"A ring of touching Euro coins" gefunden.
Sie ist offenbar nicht mehr online.
Es wäre zu überlegen,
ob man um eine feste Münze herum einen Kette aus gleichen Münzen
legen kann.
Bündel aus Fäden
top
... ... ...
|
Das Band links besteht aus vielen Fäden, die dadurch
zusammengehalten werden, dass sie verdrillt sind.
Betrachtet man den Querschnitt, so ist er als Ganzes angenähert
kreisförmig und besteht aus vielen Kreisen.
 Solche Bündel findet man vielerorts:
Solche Bündel findet man vielerorts:
Seile, Leitungsdrähte, Lichtleiter, Pflanzenstängel,
... |
twenty five top
Es gibt ein Spiel, bei dem man 25 Kreise in einen großen
Kreis einordnen muss.
... ... ... |
Der große Kreis ist eine kreisförmige Vertiefung
in einer Kunststoffplatte mit einem Durchmesser von 13,5cm.
Die kleinen Kreise sind Spielsteine in Form von unten
offenen Zylindern, die oben mit einer Halbkugel geschlossen sind.
Es gibt drei Sorten mit den ungefähren Durchmessern
2,4cm, 2,6cm und 3,1cm. Die Anzahl ist der Größe nach geordnet
14, 10 und 1.
Nebenstehend eine von wahrscheinlich vielen Lösungen.
Die farbigen Kreise sind hier ungeordnet, es gibt aber auch ein schöne
symmetrische Lösung.
All rights by RR-Trading O 67346 Speyer/Germany |
Auf dieses Spiel haben Thomas und Christoph Lohe hingewiesen,
danke.
Auf meiner Webseite Kreise
in einer Figur gibt es mehr.
Kreise im
Kreis im Internet top
Deutsch
Wikipedia
Kreispackung
in einem Kreis, Fischblase
(Ornament)
Englisch
Boris D. Lubachevsky, Ron L. Graham, Frank H. Stillinger
Spontaneous
Patterns in Disk Packings
Brady Haran (numberphile)
Epic
Circles |
Screenshot bei Youtube
|
Eric W. Weisstein
Circle
Packing,
Pappus
Chain, Steiner
Chain, Steiner's
Porism, Soddy
Circles, Apollonius
Problem, Johnson's
Theorem,
Circle-Circle
Intersection
E. Specht
The
best known packings of equal circles in the unit circle
Jos Leys
Fun
with circles
Kenneth Stephenson
Circle
Packing: A Mathematical Tale (.pdf-File)
NN
Packings of equal
and unequal circles...
R.L. Graham, B.D. Lubachevskya, K.J. Nurmelal, P.R.J.
Östergard
Dense
packings of congruent circles in a circle
(.pdf-file)
Wikipedia
Circle
packing in a circle
Referenzen top
(1) Martin Gardner: Fractal Music, Hypercards and More
Math. Recreations from SA Magazin, Freeman (1991) New York
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |






 ...
...


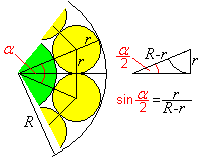 ...
...


 ...
...
 ....
.... ...
... ...
...







 ...
... ...
...
 ...
...