Was ist das Oktaeder?
...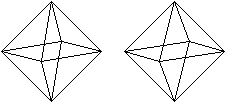 ... ... |
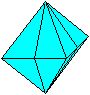
Das Oktaeder ist ein regelmäßiger
Körper, der von acht kongruenten gleichseitigen Dreiecken gebildet
wird.
| Das Oktaeder ist ein platonischer
Körper. |
 |
|
Es hat e=6 Eckpunkte, k=12
Kanten und f=8 Seitenflächen. Es gilt der eulersche Polyedersatz e+f=k+2.
Wenn man vom Wort Oktaeder
her kommt (Oktaeder heißt Achtflächner), könnte man jeden
Körper mit acht Seitenflächen Oktaeder nennen. Aber man schränkt
die Bedeutung des Oktaeders meist auf den oben beschriebenen und abgebildeten
Körper ein. Der allgemeine Körper heißt dann oft Achtflach.
Besondere
Parallelprojektionen top
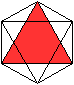
2 Dreiecke liegen parallel
zur Zeichenebene.
|
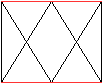
2 Dreiecke liegen senkrecht
zur Zeichenebene.
|
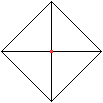
2 Eckpunkte liegen
hintereinander.
|
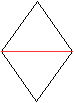
Die Mittelebene liegt
senkrecht zur Zeichenebene.
|
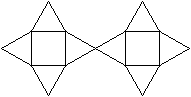
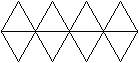
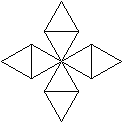
11 Netze top

|
|
|
Es gibt viele Möglichkeiten,
das Oktaeder in der Ebene auszubreiten. |
Schlegeldiagramm
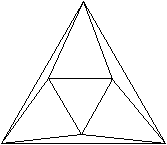
Symmetrien top
>Das Oktaeder ist symmetrisch bezüglich einer Mittelebene.
Es gibt drei Möglichkeiten.
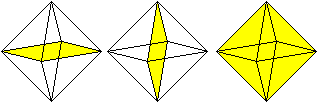
>Es ist symmetrisch bezüglich
einer Ebene durch zwei Eckpunkte und zwei Kantenmitten.
Es gibt sechs Möglichkeiten.

>Es ist drehsymmetrisch mit
der Ordnung 4 mit einer Drehachse durch zwei gegenüberliegende Eckpunkte.
Nach Drehungen um 90°, 180° oder 270° geht
das Oktaeder in sich selbst über.
Es gibt drei Möglichkeiten.
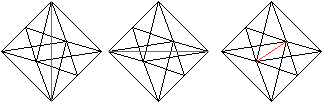
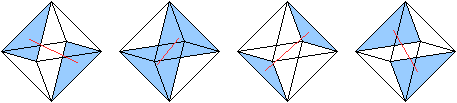
>Es ist drehsymmetrisch mit
der Ordnung 2 mit einer Drehachse durch zwei Kantenmitten.
Nach Drehungen um 180° geht das Oktaeder in sich
selbst über.
Es gibt sechs Möglichkeiten.

>Es ist drehsymmetrisch mit
der Ordnung 3 mit einer Drehachse durch zwei Mittelpunkte gegenüberliegender
Flächen.
Nach Drehungen um 120° oder 240° geht das Oktaeder
in sich selbst über.
Es gibt vier Möglichkeiten.
Größen
des Oktaeders top
Das Oktaeder hat die Kantenlänge a, das Volumen
V,
die Oberfläche O, den Radius R der Umkugel, den Radius
r
der Inkugel, Radius rk der Kantenkugel, die Dicke d,
den
Winkel zwischen zwei Seitenflächen
2*epsilon und die Raumdiagonale
e.
Wenn a die Kantenlänge ist, dann gilt
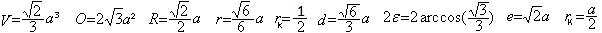
Herleitungen
Vorweg: Höhe
und Flächeninhalt des Seitendreiecks
...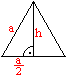 ... ... |
Ein Seitendreieck wird herausgegriffen.
Nach dem Satz des Pythagoras ist die Höhe h=(1/2)sqrt(3)a.
Die Fläche des Dreiecks ist A=(1/2)ah=(1/4)sqrt(3)a². |
Volumen
...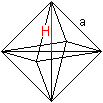 ... ... |
Das Volumen einer quadratischen Pyramide ist V'=(1/3)a²H
mit H=(1/2)sqrt(2)a.
Dann ist V=2V'=2(1/6)sqrt(2)a³=(1/3)sqrt(2)a³.
|
Oberfläche
O=8A=8*(1/4)sqrt(3)a²=2sqrt(3)a²
Radius R der Umkugel
...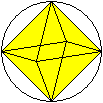 ... ...
|
Die Umkugel verläuft durch alle sechs Eckpunkte.
Der Durchmesser ist eine Diagonale in einem Quadrat mit der Seitenlänge
a.
R=(1/2)sqrt(2)a.
|
Radius
r der Inkugel
...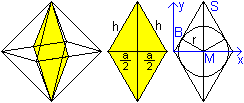 ... ... |
Die Inkugel berührt von innen alle Seitenflächen.
Zur Berechnung greift man eine Raute heraus, die durch zwei Kantenmitten
verläuft und die somit zwei Seitenlängen h=(1/2)sqrt(3)a hat.
Die Inkugel erscheint als Inkreis der Raute. Die Raute besteht aus vier
Dreiecken mit den Seitenlängen (1/2)sqrt(2)a, (1/2)a und h=(1/2)sqrt(3)a. |
Den Flächeninhalt eines Dreiecks kann man auf zwei Wegen
berechnen, nämlich
A=(1/2)(1/2)sqrt(2)a(1/2)a=(1/8)sqrt(2)a² und A=(1/2)(1/2)sqrt(3)ar=(1/4)sqrt(3)ar.
Dann ist (1/8)sqrt(2)a²=(1/4)sqrt(3)ar oder r=[(1/2)sqrt(2)]/sqrt(3)]a
oder r=[(1/6)sqrt(6)]a.
Radius
der Kantenkugel
Die Kantenkugel ist die Kugel durch alle Kantenmitten.
...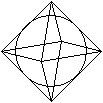 ... ... |
Man erhält den Radius, indem man ein Quadrat im
Oktaeder betrachtet und dann den Inkreis.
Der Radius ist rk = (1/2)a. |
Dicke
d
...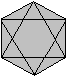 ... ... |
Man kann das Oktaeder auch auf eine Seitenfläche
stellen.
Dann erhält man in der Aufsicht ein Sechseck mit
Diagonalen als Bild des Oktaeders. |
... .... .... |
Den Abstand der parallelen Dreiecke
soll als Dicke d des Oktaeders bezeichnet werden. Es gilt d=2r=(1/3)sqrt(6)a.
In dieser Darstellung wird
deutlich, dass das Oktaeder auch ein Antiprisma ist. Zwei Dreiecke werden
parallel gestellt, gegeneinander gedreht und die Eckpunkte oben und unten
verbunden, so dass Dreiecke entstehen.
Winkel
zwischen zwei Seitenflächen
...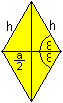 ... ... |
In der oben beschriebenen Raute taucht auch der Winkel
2*epsilon zwischen zwei Seitenflächen in Originalgröße
auf.
Es gilt cos(epsilon)=(a/2)/h=(a/2)/[(1/2)sqr(3)a]=(1/3)sqrt(3).
Das führt zu 2*epsilon=2*arc cos[(1/3)sqrt(3)] oder 2*epsilon=109,5°. |
Raumdiagonale
e=2H=sqrt(2)a.
Oktaeder durch
Formeln top
Formeln erzeugen ein Oktaeder.
1
...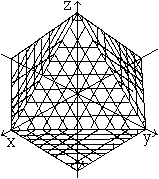 ... ... |
Es ist möglich, ein Oktaeder in einem dreidimensionalen
kartesischen Koordinatensystem durch eine Formel darzustellen.
Die Formel lautet |x|+|y|+|z|=1 oder abs(x)+abs(y)+abs(z)=1. |
2
...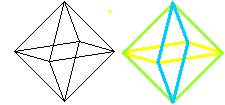 ... ... |
Ein Oktaeder kann auch aus drei Quadraten entstehen,
die in den Symmetrie-Ebenen des Oktaeders liegen. |
...
....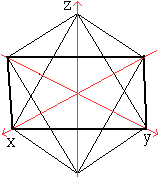 ..... ..... |
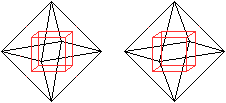
Nach diesem Vorbild kann man das Oktaeder auch so beschreiben,
dass man in jeder Hauptebene des Koordinatensystems ein Quadrat darstellt.
Die Gleichungen |x|+|y|=1, |x|+|z|=1 und |y|+|z|=1 legen
die Quadrate fest.
Das Quadrat mit |x|+|y|=1 ist fett gezeichnet. |
Zentrierte
Oktaederzahlen top
...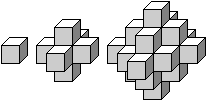 ... ... |
Man kann aus Würfeln oktaeder-förmige Körper
bauen, die je mehr zum Oktaeder werden, desto größer die Anzahl
der Würfel wird.
In der Zeichnung sind die ersten drei Körper mit
der Anzahl 1, 7, und 25 dargestellt. |
Die Zahlen heißen zentrierte
Oktaederzahlen.
Die ersten zehn Zahlen sind 1, 7, 25, 63, 129, 231, 377,
575, 833, 1159.
Raumausfüllung
top
Es gibt in der Mathematik das Problem der vollständigen
Raumausfüllung durch Körper. Bekanntlich füllen Packungen
von Würfeln den Raum aus. Das gelingt aber nicht mit den Oktaedern.
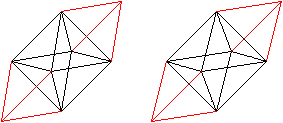
Erst wenn man eine Kombination von Oktaedern und Tetraedern
vorgibt, klappt das. Ein Oktaeder (schwarz) und zwei Tetraeder (rot) bilden
ein Parallel-Epiped. Das ist ein gereckter Würfel. So wie die Würfel
füllen auch die gereckten Würfel, die Parallelepipede, den Raum
aus.
Würfel und Oktaeder
top
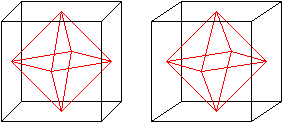
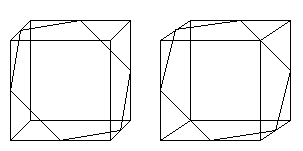
Würfel und Oktaeder sind duale
Körper.
Es gilt nämlich:
Verbindet man die Mittelpunkte der Seitenflächen
des Oktaeders, so entsteht ein Würfel.
Verbindet man die Mittelpunkte der Seitenflächen
des Würfels, so entsteht ein Oktaeder.
Das
hat offenbar Folgen.
Ecken, Kanten, Flächen
Der Würfel hat 8 Ecken, 12
Kanten und 6 Flächen.
Vertauscht man die Zahlen 8 und
6 und behält 12 bei, so erhält man die Daten des Oktaeders.
Das Oktaeder hat 6 Ecken, 12 Kanten
und 8 Flächen.
Besondere
Ansichten
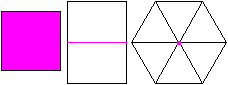
Würfel
|
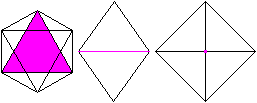
Oktaeder
|
Eine Seitenfläche, eine Kante
und eine Ecke liegen vorne.
Symmetrien
Der Würfel und das Oktaeder
haben neun Symmetrieebenen.
Netze
Das Oktaeder und der Würfel haben 11 Netze.
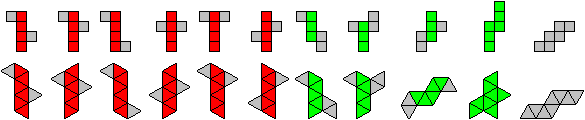 Die Farben zeigen den Versuch, die Netze einander zuzuordnen.
Die Farben zeigen den Versuch, die Netze einander zuzuordnen.
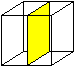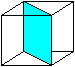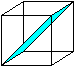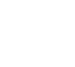
Sechseck
im Oktaeder und im Würfel
In den Mittelpunkten von sechs Kanten liegen die Eckpunkte
eines regelmäßigen Sechsecks.
Verschiedene Körper
top
Oktaeder im Tetraeder
...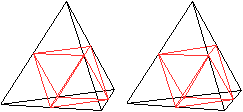 ... ... |
Verbindet man die Mittelpunkte von sechs Kanten eines
Tetraeders,
so entsteht ein Oktaeder. |
Kuboktaeder
...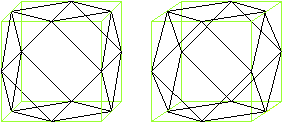 ... ... |
Das Kuboktaeder
entsteht, wenn man von einem Würfel an den Ecken acht Pyramiden abschneidet.
Diese Eckpyramiden zusammen können zu einem Oktaeder
werden. |
...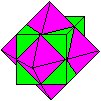 ... ... |
Das Kuboktaeder ist
der Kern eines Würfel und eines Oktaeders. |
Das Kuboktaeder ist einer der 13 Archimedischen
Körper.
Abgestumpftes
Oktaeder
Man schneidet die acht Ecken eines
Oktaeders ab. Dazu teilt man jede Kante in drei gleiche Teile.
(Beim Kuboktaeder oben halbiert
man die Kanten.)
Es entsteht ein Körper, der von sechs Quadraten und
acht regelmäßigen Sechsecken begrenzt wird.
Das abgestumpfte
Oktaeder gehört auch zu den 13 archimedischen Körpern.
Triakisoktaeder
...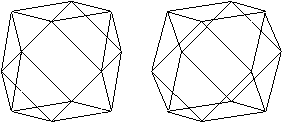 ... ... |
Verbindet man benachbarte Mittelpunkte der gleichseitigen
Dreiecke und Quadrate des Kuboktaeders, entsteht als dualer Körper
das Triakisoktaeder.
Ich verzichte darauf, das auch wirklich zu tun. Auf meiner
Webseite
Triakistetraeder habe ich diese
aufwändige Prozedur dargestellt. |
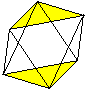
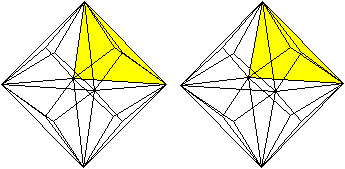
Das Ergebnis ist ein Oktaeder,
auf dessen Seitenflächen Dreieckspyramiden liegen.
Eine Pyramide ist in der folgenden Zeichnung mit Gelb
hervorgehoben.
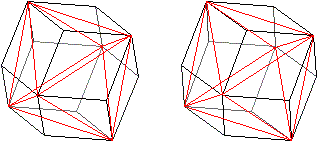
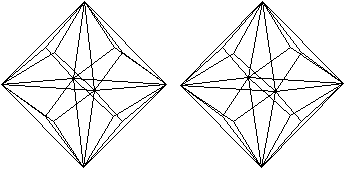
Zwei
Erweiterungen des Triakisoktaeders
>Man kann die Höhe der Dreieckspyramide so vergrößern,
dass zwei nebeneinander liegende Dreiecke zu einer Raute werden.
Aus dem Triakisoktaeder wird dann ein Rhombendodekaeder.
... ... ...
|
|
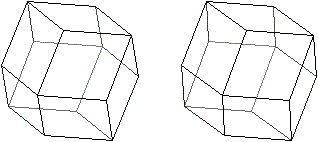
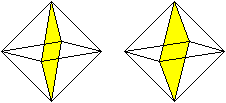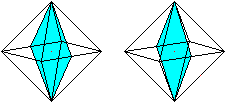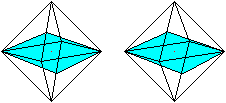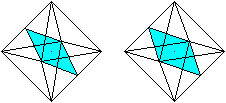
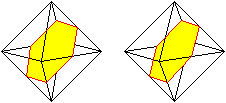
>Vergrößert man
die Höhe noch weiter, so können aus den Dreieckspyramiden Tetraeder
werden. Der Körper ist dann ein Oktaeder, auf dessen acht Seitenflächen
Tetraeder liegen. Das Ergebnis ist der Oktaederstern aus 24 gleichseitigen
Dreiecken. Er zählt zu den konkaven Deltaedern.
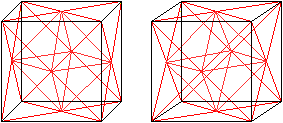
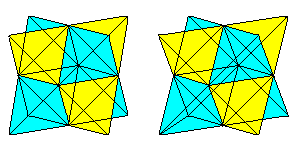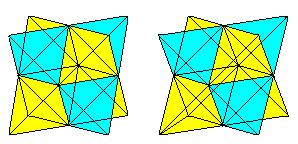
Oktaeder
im Ikosaeder
...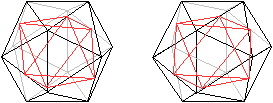 ... ... |
Verbindet man sechs bestimmte Mittelpunkte von Kanten
des Ikosaeders, so entsteht ein Oktaeder. Es gibt fünf Möglichkeiten,
ein Oktaeder in das Ikosaeder zu legen.
Zeichnet man alle Oktaeder ein, so entsteht ein Sternkörper.
Er ist auf der Webseite unter "Octahedron 5-Compound" bei MathWorld (URL
unten) dargestellt. |
Für den Fall Tetraeder
im Pentagondodekaeder habe ich einen ähnlichen Stern ausführlich
entwickelt.
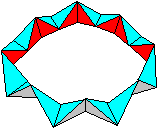
Boot
...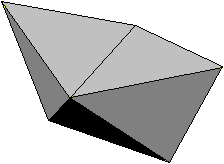 ... ... |
Das Boot ist hier ein geometrischer Körper, der
von 8 gleichseitigen Dreiecken gebildet wird.
Ein (schwarzes) Tetraeder balanciert auf einer Kante,
rechts und links wird je ein Tetraeder aufgesetzt.
Und was hat dieser Körper mit einem Oktaeder zu tun? |
Das
ist eine Kuriosität: Das Boot hat mit dem Oktaeder ein Netz gemeinsam.
Entdeckt bei MathWorld (URL unten)
Ein
Kaleidozyklus
Oktaeder-Ball
...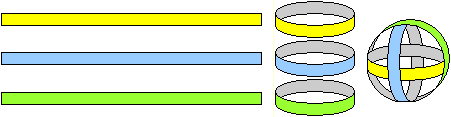 ... ... |
Man formt aus drei Streifen Ringe und klebt die Enden
zusammen. Dann steckt man sie so ineinander, dass sie in die drei Richtungen
des Raumes zeigen. Es entsteht der Oktaederball. |
Mehr auf der Seite Körper
flechten
Kleines
Rhombenkuboktaeder
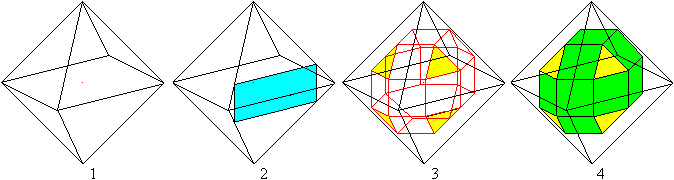 Mehr auf meiner Seite Kleines
Rhombenkuboktaeder
Mehr auf meiner Seite Kleines
Rhombenkuboktaeder
Eulerweg
In jedem Eckpunkt eines Oktaeders treffen vier Kanten
zusammen. Deshalb ist ein Eulerweg möglich.
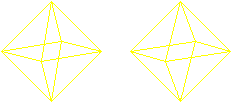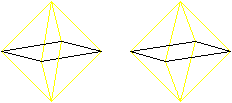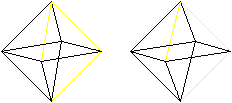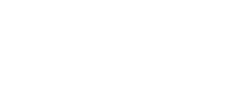
Mehr über den Eulerweg findet man auf meiner Seite
Haus
des Nikolaus.
Basteleien top

Papier und Kleber
|

Zahnstocher und Bostik
|

Kugeln und Stabmagnete
|
Oktaederstern als Bascetta-Stern
Freundlicherweise zur Verfügung gestellt von Rudolf
Kunstmann
Oktaeder im Internet
top
Deutsch
Gerd Müller
Platonische
Körper in Stereodarstellung
H. B. Meyer (Polyeder aus Flechtstreifen)
Oktaeder
Udo Hebisch
Oktaeder
Wikipedia
Oktaeder,
Triakisoktaeder,
Hexaederstumpf,
Oktaederstumpf,
Kuboktaeder,
Sterntetraeder,
Oktaedergruppe
Englisch
Eric W. Weisstein
Octahedron,
Truncated
Octahedron, Cuboctahedron,
Boat,
Octahedral
Number, Octahedron5-Compound
G. Korthals Altes
Paper
model Octahedron
H. B. Meyer (Polyeder aus Flechtstreifen)
Octahedron
OEIS
A005900 Octahedral
numbers: (2n^3 + n)/3.
A001845 Centered
octahedral numbers
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Octahedron,
Triakis
octahedron,
Truncated
cube,
Truncated
octahedron,
Cuboctahedron,
Octahedral
number, Octahedral
symmetry
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage: https://www.mathematische-basteleien.de/
©
2004, überarbeitet 2012, Jürgen Köller
top |







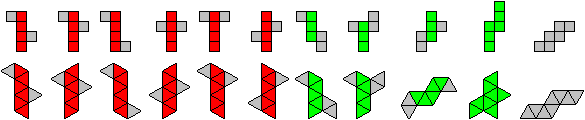


 ...
...








 ...
... ...
... ...
... ...
... ...
... ...
... ....
.... ...
... ...
... ...
... .....
..... ...
...


 ...
... ...
... ...
...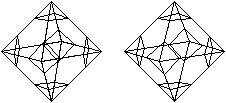
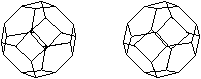
 ...
...
 ...
...
 ...
... ...
...


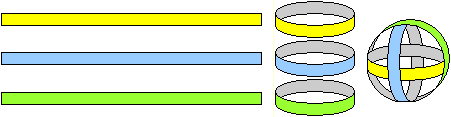 ...
...




