|
Was ist der Würfel? top
Der Würfel ist ein von sechs
gleichen Quadraten begrenzter mathematischer Körper.
Er heißt auch Kubus, Hexaeder
oder Sechsflach.
... ...
|
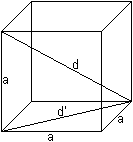
Der Würfel hat 12 gleich lange
Kanten.
Drei Kanten treffen sich in einer
Ecke und stehen paarweise aufeinander senkrecht.
Die Länge einer Kante sei
a. Dann gilt:
Der Würfel hat 12 Flächendiagonalen
der Länge d' = sqr(2)a.
Der Würfel hat 4 Raumdiagonalen
der Länge d=sqr(3)a.
Das Volumen beträgt V=a³,
die Oberfläche O=6a².
Die Umkugel hat den Radius R = (1/2)sqrt(3)a, die Inkugel
den Radius r = (1/2)a.
Der Kantenkugel (Kugel durch die Kantenmitten) hat den
Radius rk = (1/2)sqrt(2)a. |
Im täglichen Sprachgebrauch
ist der Würfel meist der Spielwürfel.
In den achtziger Jahren war der Zauberwürfel (Rubik's
cube) so populär, dass er einfach "der Würfel" hieß.
Ansichten eines
Würfels
top
Schrägbild
... ... |
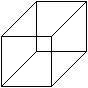Wenn man Schüler bittet das Schrägbild eines
Würfels zu zeichnen und vorher darauf hinweist, dass beim Würfel
alle Seiten gleich lang sind, entsteht bei einigen die nebenstehende Zeichnung.
Man hat aber nicht den Eindruck, dass es sich hier um
die Darstellung eines Würfels handelt. Es ist eher eine quadratische
Säule. Die schrägen Linien müssen offenbar verkürzt
werden. |
Es stellt sich die Frage, wie stark
verkürzt werden muss, um ein anschauliches Bild zu erreichen. Stellt
man die folgenden vier Schrägbilder zur Auswahl, bei denen in der
Zeichnung der Abstand der beiden rechten vertikal liegenden Kanten 2, 3,
4 und 5 Längeneinheiten ist, so tippen die meisten auf Bild 3 als
bestes Bild eines Würfels.
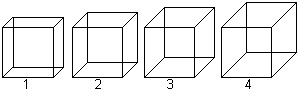Man misst nach, dass die schräge Strecke des Körpers
3 etwa halb so groß wie die wahre Länge der Kante ist. So gelangt
man zum üblichen Verkürzungsfaktor k=1/2.
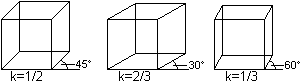
Der Verkürzungsfaktor
hängt davon ab, wie schräg die Kanten liegen. Die folgenden drei
Festsetzungen ergeben brauchbare Bilder eines Würfels.
Die mathematische Grundlage ist die schräge Parallelprojektion
eines Würfels, bei der je nach Beleuchtung alle Winkel und Verkürzungsfaktoren
möglich sind. Man entscheidet sich für einfache Winkel und einfache
Verkürzungsfaktoren (2).
Es gilt der Satz von Pohlke (oder Hauptsatz der Axonometrie):
Jedes ebene, echt zweidimensionale ,,Dreibein" OABC kann
als Parallelprojektion eines räumlich-kartesischen Dreibeins O'A'B'C'
erhalten werden. (Quelle: http://www.math-inf.uni-greifswald.de/mathematik+kunst/themen.html)
Weitere Schrägbilder
| ...... |
Die nebenstehende Zeichnung mit gleich langen Kanten
war als Schrägbild eigentlich nicht zu gebrauchen. Die Bildwirkung
ist nicht gut. Trotzdem wird sie verwendet. Sie hat nämlich den Vorteil,
dass man Strecken in Richtung der Kanten ohne Umrechnung übernehmen
kann. - Die "isometrische Kavaliersperspektive" (statt 45° nimmt man
30°) ist nicht so verzerrt und wird deshalb bevorzugt. |
Zentralprojektion
... ... |
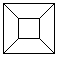Man stelle sich das Kantenmodell eines Würfels vor.
Durchstrahlt man es mit Licht, das von einer punktförmigen
Lichtquelle ausgeht, so kann in der Projektion das nebenstehende Bild eines
Würfels entstehen. |
Netze eines
Würfels
... ... |
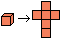Man denke sich einen Würfel aus Papier und schneide
ihn an den Kanten auf: Es entstehen Netze eines Würfels. Es gibt 11
verschiedene Netze. |
... ... |
Stereogramm
Mit dem 3-D-Blick sieht man den Würfel dreidimensional.
(Mehr auf meiner Seite Stereogramm)
Schattenrisse
eines rotierenden Würfels
 |
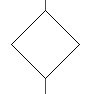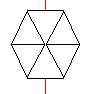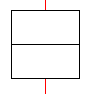Das Deutsche Museum in München beherbergt seit einigen
Jahren "das Mathematische Kabinett". Ein schönes Ausstellungsstück
ist ein sich drehendes Kantenmodell des Würfels, das parallel durchstrahlt
wird und das auf einer Leinwand der Reihe nach die nebenstehenden einfachen
Figuren (Quadrat auf der Spitze, Hexagon mit Diagonalen und Rechteck mit
einer Mittellinie) erzeugt.
Man glaubt nicht, dass diese Figuren vom Würfel
stammen und muss schon zweimal hinsehen. Das Kantenmodell ist so ausgerichtet,
dass zwei gegenüberliegende Kanten übereinanderliegen. Durch
sie verläuft die innen unterbrochene Drehachse (hier rot). |
Bau eines Würfels
top
Flächenmodell
... ...
|
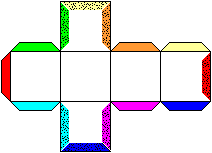
Dieses ist die übliche Art einen Würfel zu
bauen.
Man zeichnet ein Netz und versieht gewisse Ränder
mit Klebestreifen.
Die Streifen werden abgeknickt und innen auf die gepunkteten
Felder gleicher Farbe geklebt. Der Würfel wird zuletzt mit dem Deckel
rechts geschlossen. |
Kantenmodelle
Es gibt unterschiedliche Möglichkeiten, Würfel
aus Stäben zu bauen.
>Man kratzt von Streichhölzern die Köpfe
ab und verbindet die Streichhölzer mit Zweikomponentenkleber.
>Man verwendet Zahnstocher oder Schaschlikstäbe
und verbindet sie mit Kügelchen aus Kitt oder Knetgummi.
>Man kneift mit einer Zange gleich lange gerade
Drähte ab und lötet die Enden zusammen, so dass ein Würfel
entsteht. Es empfiehlt sich, die drei Drahtenden, die eine Ecke bilden
sollen, vor dem Löten auszurichten und sich berühren zu lassen.
Das schafft man z.B. mit der "helfenden Hand", die aus zwei Krokodilklemmen
besteht, und mit einer wahren Hand.
>Man schneidet Trinkhalme in gleich lange Stücke
und verbindet sie mit Dreibeinen aus Blumendraht oder dem Draht einer Büroklammer.
Genauer: Es gibt Bausätze für mathematische
Körper, die 12 Trinkhalme und 8 Dreibeine aus Plastik für den
Bau eines Würfels verwenden (Unten wurde ein Dreibein aus einer
Ecke herausgenommen, rot). Diese Dreibeine kann man aus einem Stück
Draht selbst herstellen (unten, dunkelgrün). Man biegt ihn doppelt
in 6 Teilabschnitte. In den Spitzen liegen Biegungen, die beiden Enden
des Drahtes stoßen in der Mitte zusammen.
... ... |
Es gibt ein pfiffiges Modespielzeug, das seit einigen
Monaten in vielen Spielzeugläden auf den Ladentischen ausliegt. Stabmagnete
bilden die Kanten, Stahlkugeln die Verbindungsstücke.
Der Bausatz für einen Würfel kostet 14€
(Frühjahr 2002). Es ist anzunehmen, dass er billiger werden wird,
sobald er von den Ladentischen in die Regale wandern wird ;-). |
Symmetrien eines
Würfels
top
Der Mittelpunkt des Würfels
ist das Symmetriezentrum.
... ...
|
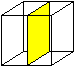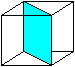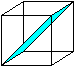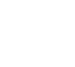
Der Würfel hat neun Symmetrieebenen.
Drei Ebenen liegen parallel zu den Seitenflächen
und gehen durch die Mitte (Bild).
Sechs Ebenen gehen durch gegenüberliegende Kanten
und zwei Raumdiagonalen. Sie zerschneiden den Würfel in Prismen. |
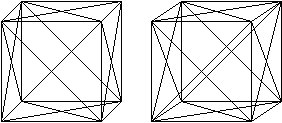
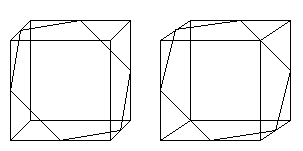
Man kann 13 Drehachsen finden. Dreht
man um eine dieser Achsen, so geht er in sich selbst über und zeigt
neue Ansichten.
Das folgende Bild illustriert diesen Sachverhalt. Die
Zahlen unter den Würfeln geben die Anzahl der Drehungen an.
Innenansichten
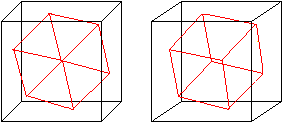
eines Würfels top
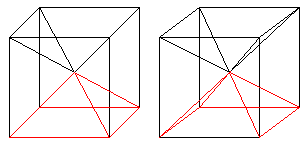
Alle Flächendiagonalen
des Würfels
Alle Raumdiagonalen
des Würfels
Abgestumpfter
Würfel
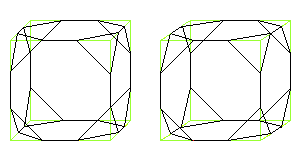
Stumpfe den Würfel an den Ecken ab. Eine Kante wird
dazu gedrittelt.
Es entsteht ein Körper mit
6 Achtecken und 8 gleichseitigen Dreiecken.
Teilt man die Würfelkanten
im Verhältnis sqrt(2):2:sqrt(2), so hat der abgestumpfter
Würfel gleiche Kanten.
Er gehört zu den archimedischen
Körpern.
Kuboktaeder
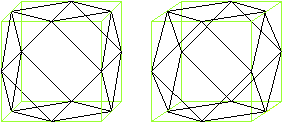
Stumpfe den Würfel an den Ecken stärker ab.
Eine Kante wird dazu halbiert.
Es entsteht ein Körper mit
6 Quadraten und 8 gleichseitigen Dreiecken.
Auch das Kuboktaeder
gehört zu den archimedischen Körpern.
Das Tetraeder
im Würfel
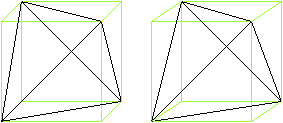
Zeichne bestimmte Flächendiagonalen ein. Es entsteht
ein Tetraeder.
Das Oktaeder
im Würfel
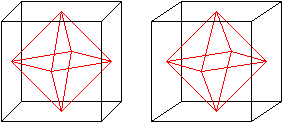
Verbinde die Mittelpunkte der Seitenquadrate eines Würfels.
Es entsteht ein Oktaeder.
Weiter: Verbindet man die Mittelpunkte der Seitenflächen
eines Oktaeders, so entsteht wieder ein Würfel.
Würfel und Oktaeder sind duale Körper.
Drei Pyramiden
gleichen
Volumens im Würfel
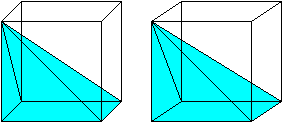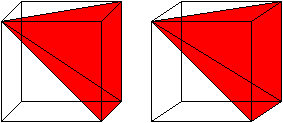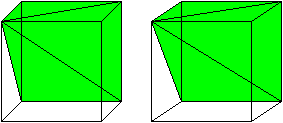
Das größte
Quadrat im Würfel
Das rote Quadrat ist das größte Quadrat, das
in einen Würfel passt.
Die Eckpunkte des Quadrates teilen die Kanten im Verhältnis
1:3. (1)
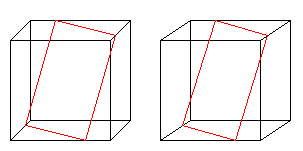
Der Würfel
im Würfel
Der rote Würfel ist der kleinste Würfel, der
alle Seitenflächen des schwarzen Würfels berührt (mehr auf
der Webseite 4).
Das Hexagon
im Würfel
Verbinde gewisse Kantenmitten. Es entsteht der Schnitt
durch einen Würfel.
Schnittlinie ist ein Hexagon der Kantenlänge (1/2)sqr(2)a,
wenn a die Kante des Würfels ist.
Ein räumliches
gleichseitiges Sechseck
Delisches
Problem (Problem der Würfelverdoppelung) top
Der Sage nach sollten die Griechen
nach einer Antwort des Orakels auf Delos von der Pest befreit werden,
wenn sie den würfelförmigen Altar des Apollo doppelt so groß
machten. (Dieses ist eine Version der Geschichte.)
... ... |
Das Problem der Würfelverdoppelung
führt mit dem Ansatz 2a³=x³ zur Lösung x=2^(1/3)a.
Für die Griechen galt dies nicht als Lösung, denn die Strecke
x musste nur mit Zirkel und Lineal aus der Strecke a ermittelt werden.
Man weiß heute, dass diese Aufgabe unlösbar ist, denn nur Terme
mit Quadratwurzeln sind konstruierbar. Kreise und Geraden führen nämlich
zu linearen und quadratischen Gleichungen, zu denen x³=2a³ nicht
gehört. |
Auch zwei andere Probleme sind aus
im Prinzip gleichen Gründen unlösbar: Die Verwandlung des Kreises
in ein flächengleiches Quadrat ("Quadratur des Kreises") und die Teilung
eines beliebigen Winkels in drei gleiche Teile ("Dreiteilung eines Winkels").
Polykuben top
Man kann Polykuben bilden, indem man Würfel an einer
oder mehreren Quadratflächen zusammenfügt.
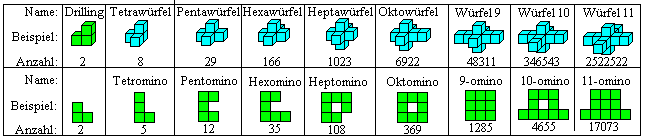
Die Zahlen geben die Anzahl der jeweiligen Würfelkörper
einer Sorte an. (3)
Es gibt zahlreiche Puzzles auf der
Basis der Polykuben. Hier ist meine "Hitliste":
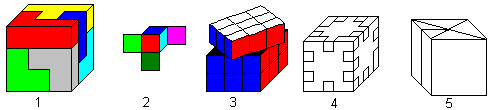
Sie werden an anderer Stelle dieser Homepage beschrieben.
Es handelt sich um 1 Somawürfel, 2 Mac
Mahons Farbwürfel, 3 Zauberwürfel
(Rubik's Cube), 4 Happy Cube und 5 Origami-Würfel.
Weitere Würfelseiten behandeln Tetrawürfel,
Hexominos,
Schlangenwürfel,
Magischer
Würfel, Wunderwürfel (und
Spielwürfel).
Hyperkubus (vierdimensionaler
Würfel)
top
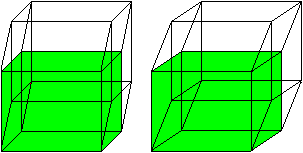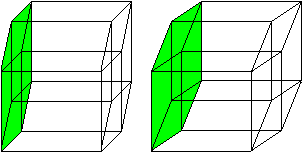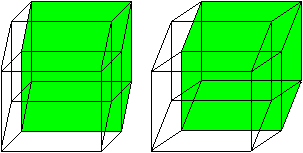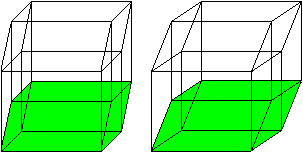Er wird auf meiner Webseite Hyperkubus
beschrieben.
Optische
Täuschungen mit Würfeln top
Wenn man so will, ist jede Darstellung
eines Würfels in der Ebene eine optische Täuschung. Man glaubt,
den dreidimensionalen Würfel zu sehen, obwohl die Zeichenebene zweidimensional
ist.
Bekannte Sinnestäuschungen
mit Würfeln sind die "Kippfiguren", auf die ich mich beschränke.
... ... |
Beim Neckerwürfel wird ein Würfel in zwei Perspektiven
gezeigt (links).
Man schaltet von einer Ansicht in die andere um. Eine
Ecke ist mal hinten und mal vorne. Man kann immer nur eine Ansicht wahrnehmen. |
... ... |
Bei den folgenden Bildern stellen sich die Fragen:
Rechts oder links? Von unten oder von oben?
Drei oder fünf Würfel? Fünf oder drei Würfel?
Wie viele Würfel?
Die fünf Bilder oben sind doppeldeutig. Man sieht
die Würfel entweder von oben oder von unten.
Schaut man auf einen Turm oder in ein Loch?
Der Würfel
als Bauwerk
top
Ein Gebäude in Würfelform ist nicht praktisch.
Vielleicht haben gerade deshalb Architekten und Künstler den Würfel
als Herausforderung angenommen, um kreativ zu werden. Die Ergebnisse
sind viele originelle Schaubauten und Skulpturen in aller Welt.
Hier ein kleiner Rückblick auf die denkwürdige
Expo 2000 in Hannover.
1 Der T-Digit der Deutschen Telekom bildete ein Zentrum
des Ausstellungsgeländes. Von einer breiten Schautreppe aus konnte
man auf eine Projektionsfläche herabsehen, wo (sogar im Sonnenschein)
ein beeindruckend helles Fernsehbild (hier der Tennisplatz zum French Open
in Paris) zu sehen war.
2 Der Ausstellungsblock des mexikanischen Pavillons
bildete einen Würfel, der weithin sichtbar war.
3 Unvergessen ist der isländische Kubus. Er
war in Dunkelblau gehalten und über ihm lag ein Wasserfilm. Innen
stand ein rundes Wasserbecken, dessen Oberfläche als Projektionsfläche
für einen Film über Island aus der Vogelperspektive diente. Am
Ende der Vorführung schoss ein künstlicher Geysir in die Höhe.
4 Ich habe vergessen den norwegischen Würfelbau
mit dem Wasserfall zu fotografieren :-(.
... ... |
Deshalb begnüge ich mich mit dem Bild eines Modells,
das schon vor der Expo-Eröffnung im Internet stand. Ganz so mächtig
ist der Wasserfall dann nicht geworden.
Nach einer leichten Dusche gelangte man in den "Raum der
Stille". Man konnte etliche Minuten lang auf dem harten Fußboden
sitzen und sich den Naturdarstellungen auf allen sechs Innenwänden
hingeben. Ab und zu kullerten (nur akustisch angedeutet) Steine den Fels
hinunter. Sprechen war nicht erwünscht. Meine Frau ... (Zensur!) |
Hinweis
Der Origami-Würfel ist ein Würfel, der aus
einem quadratischen Blatt Papier gefaltet wird.
Auf meiner Webseite Origami-Würfel
findet man viele Würfel dieser Art.
... |
 |
Der
Würfel im Internet top
Deutsch
H. B. Meyer (Polyeder aus Flechtstreifen)
Hexaeder,
Würfel
(spezial)
Richard Mischak
Würfel
Wikipedia
Würfel
(Geometrie), Platonischer
Körper, Delisches
Problem, Expo
2000
Englisch
David Eppstein (Geometry Junkyard)
Box
in a Box
Easy Origami (Youtube)
Origami:
Simple Modular Cube
Eric Weisstein (MathWorld)
Cube,
Prince
Rupert's Cube
H. B. Meyer (Polyeder aus Flechtstreifen)
Cube,
Cube
(special)
Wikipedia
Cube,
Platonic
solid,
Doubling
the cube,
Expo 2000
Referenzen top
(1) Martin Gardner: Mathematischer Karneval, Ullstein
Berlin 1977 (Seite 61)
(2) Hans Simon, Kurt Stahl: Mathematik, Formeln und Gesetze,
Leipzig 1979 (Seite 471ff.)
(3) Michael Keller (früher: http://members.aol.com/wgreview/polyenum.html)
(4) David Eppstein (http://www.ics.uci.edu/~eppstein/junkyard/box-in-box.html)
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |
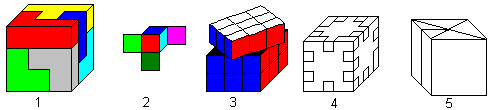