Was
ist ein Flexagon?
Ein Flexagon ist ein Sechseck,
das man aus einem Streifen aus gleichseitigen Dreiecken faltet. Der Gag
besteht darin, dass man das Sechseck in der Mitte öffnen kann. Es
erscheint ein neues Sechseck, das vorher verborgen war.
Anleitung
zum Bau eines Trihexaflexagons top
(1) Zeichne mit Hilfe von Zirkel und Lineal einen Streifen
aus 10 gleichseitigen Dreiecken.
Wähle als Seitenlänge eines Dreiecks 4 cm.
Dann passt der Streifen quer auf ein Blatt DIN A 4.
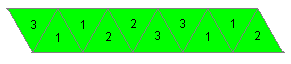 (2) Nummeriere die Dreiecke wie angegeben.
(2) Nummeriere die Dreiecke wie angegeben.
(3) Zeichne mit Hilfe eines leeren Kugelschreibers die
Seiten der Dreiecke nach, damit man das Papier an diesen Stellen später
besser falten kann.
(4) Schneide den Streifen aus.
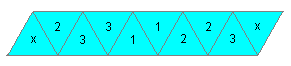 (5) Drehe den Streifen um. Nummeriere die Dreiecke wie angegeben.
Setze die beiden Kreuze. Hinter 3 liegt x, hinter 1 liegt 2 usw.. Die beiden
angekreuzten Dreiecke werden später aufeinander geklebt und
verschwinden. Knicke das Papier mehrmals an den Linien zwischen den Dreiecken,
damit das Flexagon, wenn es später zusammengebaut ist, "elastischer"
ist.
(5) Drehe den Streifen um. Nummeriere die Dreiecke wie angegeben.
Setze die beiden Kreuze. Hinter 3 liegt x, hinter 1 liegt 2 usw.. Die beiden
angekreuzten Dreiecke werden später aufeinander geklebt und
verschwinden. Knicke das Papier mehrmals an den Linien zwischen den Dreiecken,
damit das Flexagon, wenn es später zusammengebaut ist, "elastischer"
ist.
top
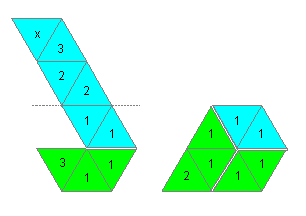 (6) Falte das Papier so, dass ein Haken entsteht. Dann falte
an der gestrichelten Linie nach hinten. Achte darauf, dass vorne nur 1
und hinten nur 2 steht. Lege dazu die Dreiecke 3 und 3 aufeinander.
(6) Falte das Papier so, dass ein Haken entsteht. Dann falte
an der gestrichelten Linie nach hinten. Achte darauf, dass vorne nur 1
und hinten nur 2 steht. Lege dazu die Dreiecke 3 und 3 aufeinander.
(7) Es entsteht ein Sechseck. Dreieck 2 steht noch über.
Es müsste auf der Rückseite ein Kreuz tragen. Klebe die beiden
Dreiecke mit den Kreuzen aufeinander.
Das Trihexaflexagon ist fertig.
Linksdrehendes Flexagon
...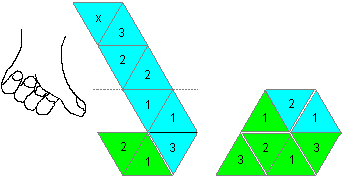 ... ... |
Man kann ein Trihexaflexagon auch erzeugen, wenn man
für den Haken die unteren drei Dreiecke nach unten hin wegklappt und
dann an der gestrichelten Linie vier Dreiecke nach vorne legt und schließlich
die linken, sichtbaren Dreiecke 2 und 3 aufeinander klebt.
Man nennt dieses Flexagon ein linksdrehendes Flexagon.
Zeigt nämlich der Daumen der linken Hand (Bild) in Richtung des Streifen,
so geben die Finger die Klapprichtung an.
Oben ist ein rechts drehenden Flexagon, da man dort die
rechte Hand nehmen muss. |
Nur rechtsdrehende Flexagons sind üblich.
Öffnen eines
Flexagons
top
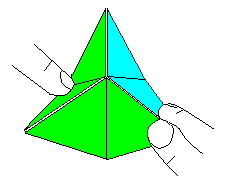 |
Das Öffnen ist beim ersten Mal eine knifflige Angelegenheit.
Fasse mit Zeigefinger und Daumen der rechten Hand zwei
Dreiecke von oben. Drücke sie nach unten. Drücke gleichzeitig
mit dem Zeigefinger der linken Hand an der gegenüberliegenden Ecke
des Sechsecks zwei Dreiecke, die eine Raute bilden, weit nach unten zur
räumlichen Achse hin. Das Sechseck lässt sich jetzt "wie eine
Blume" öffnen. Es erscheint das Sechseck mit den Dreiecken Nr.3. |
Für das systematische Öffnen eines Flexagons
kann man zwei Techniken anwenden.
Bei der "Schaukel" hält man die Begrenzungslinie
zweier Dreiecke horizontal und öffnet abwechselnd rechts und links.
Bei der "Tuckerman Traverse" dreht man nach jedem Öffnen das Flexagon
im oder entgegen dem Uhrzeigersinn weiter.
Im Folgenden soll für das Öffnen auch der Name
"Zug" gewählt werden.
Das Trihexaflexagon
top
Wie der Streifen zeigt, besteht das Trihexaflexagon aus
neun Dreiecksblättern mit Vorder- und Rückseite, also aus insgesamt
18 Dreiecken. Die Dreiecke zum Kleben zählen nicht.
Zusammengefaltet liegen jeweils zwei Dreiecksblätter
übereinander, dazwischen liegt ein einzelnes Dreiecksblatt. Die Dreiecke
haben also die Verteilung 1+2+1+2+1+2.
Zwei Dreiecksblätter sind zusammenhängend und
bilden eine Raute.
Ein Sechseck besteht aus drei Rauten.
Bei jedem Zug wird eine Raute nach außen weggeklappt
und gelangt an gleicher Stelle auf die Rückseite. Bei einem weiteren
Zug werden die beiden Dreiecke dieser Raute aufeinander geklappt.
Die Dreiecke wandern um ein Sechstel einer Volldrehung
weiter.
.. ...... ...... ... ... |
Man kennzeichnet ein Dreiecksblatt mit einer Büroklammer.
Wendet man jetzt die Schaukel an, so wandert die Büroklammer und damit
das Dreieck entgegen dem Uhrzeiger im Kreis herum, obwohl man das Flexagon
nicht dreht. |
Jedes Dreieck wird an einer Stelle dreimal geklappt und dabei
gedreht, ehe es weiterwandert.
Man braucht insgesamt 18 Züge für einen vollen
Umlauf.
Öffnet man das Flexagon nach Art der Schaukel, so
folgen die Sechsecke in der Reihenfolge 1/2/3/1/2/3/1/2/3... .Das Zeichen
/ beschreibt einen Seitenwechsel. Bei jedem Zug gelangt eine Nummer von
der Vorderseite auf die Rückseite. Dreht man das Flexagon um und öffnet,
so folgen die Sechsecke in der Reihenfolge 1/3/2/1/3/2/1/3/2...
Triflexagon mit einem Muster
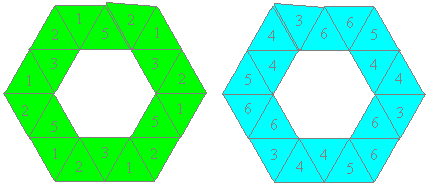
 Wenn man die gleichseitigen Dreiecke des Streifen mit Hilfe
des Mittelpunkts in drei gleiche Teile teilt und passend färbt, so
erhält man ein Trihexaflexagon mit drei schönen Mustern. Die
Ober- und Unterseite sind jeweils gleich.
Wenn man die gleichseitigen Dreiecke des Streifen mit Hilfe
des Mittelpunkts in drei gleiche Teile teilt und passend färbt, so
erhält man ein Trihexaflexagon mit drei schönen Mustern. Die
Ober- und Unterseite sind jeweils gleich.
Diese Ausführung des Trihexaflexagons stammt von
Krino Hoogestraat aus Emden.
Das Tetrahexaflexagon
top
Das Tetrahexaflexagon hat vier Oberflächen und ist
etwas komplizierter als das Trihexaflexagon.
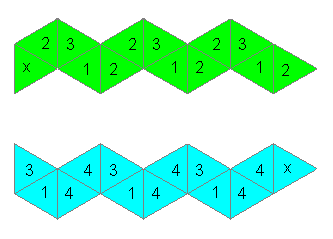 |
Zum Bau des Tetrahexaflexagons stellt man nebenstehenden
Streifen aus gleichseitigen Dreiecken her. Man nummeriert die Dreiecke
auf Vorder- und Rückseite wie angegeben.
Legt man die Dreiecke mit den Nummern 4 aufeinander, so
erhält man den Streifen des Trihexaflexagons von oben mit gleicher
Nummerierung. Man faltet ihn entsprechend. Man achtet wieder darauf, dass
die Dreiecke Nr.3 aufeinander gelegt werden. Zum Schluss klebt man die
beiden angekreuzten Dreiecke aufeinander. |
| top
Öffnet man dieses Flexagon nach Art der Schaukel,
so erhält man nacheinander die Sechsecke 1/3/2/1/3/2/1/3... (evtl.
das Flexagon umdrehen).
Man muss, um auch an das Sechseck Nr.4 zu gelangen, die
Technik der Schaukel erweitern. Man öffnet auf jeder Seite so lange,
bis es nicht mehr geht. Auf diese Weise erhält man die Reihenfolge
1/34/1/32/1/34/1/32/..., also auch das fehlende Sechseck 4. Der Schrägstrich
gibt jeweils den Wechsel rechts/links oder links/rechts an.
Es wiederholt sich die Folge 1/34/1/32/. Die Zahlen 1
und 3 kommen in dieser Periode zweimal vor, die Zahlen 2 und 4 nur einmal. |
Als mögliche graphische
Darstellungen dieser Struktur dienen ein Viereck mit Doppeldiagonale oder
zwei Dreiecke, die einen Punkt gemeinsam haben.
In der (üblichen) Darstellung rechts wird berücksichtigt,
dass das Sechseck 3 die Eigenschaft zweier Dreieckspitzen (wie 2 und 4)
hat und dass Sechseck 1 Durchlaufstation ist.
Bei Ausführung der Schaukel umläuft man in der
rechten Graphik die Gesamtfigur in Pfeilrichtung entgegengesetzt dem Uhrzeigersinn.
Zählt man die übereinander liegenden Dreiecksblätter
des Tetrahexaflexagons, so haben die Blätter der Sechsecke 2,3 und
4 die Verteilung 1+3+1+3+1+3, nur Sechseck 1 hat die Verteilung 2+2+2+2+2+2.
Das bestätigt noch einmal die Eigenschaft einer Durchlaufstation von
1.
Man könnte meinen, das Sechseck Nr.1 sei bevorzugt.
Aber dreht man das Flexagon um und öffnet fortwährend, so tauschen
1 und 3 ihre Rollen. Die Symmetrie bleibt bewahrt.
Man kennzeichnet ein Dreiecksblatt mit einer Büroklammer.
Wendet man jetzt die Schaukel an, so wandert die Büroklammer und damit
das Dreieck im Kreis herum, obwohl man das Flexagon nicht dreht. Jedes
Dreieck wird abwechselnd zwei- oder viermal an einer Stelle geklappt, ehe
es weiterwandert. Man braucht insgesamt 18 Züge für einen vollen
Umlauf.
Auch bei Anwendung der Tuckerman Traverse zeigt sich die
gleiche Struktur. Um alle Oberflächen zu erreichen, muss man - solange
es geht - öffnen und dann erst drehen.
Höhere Flexagons
top
Neben den beiden beschriebenen Flexagons gibt es Erweiterungen
auf 5, 6, ... Oberflächen, die dann entsprechende Namen Pentahexaflexagon,
Hexahexaflexagon u.s.w. tragen.
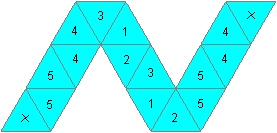
Pentahexaflexagon
|
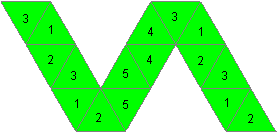
horizontal gespiegelt:
|
134/1/32/15/2/ :||
Legt man die Dreiecke mit
den Nummern 5 aufeinander, so erhält man die Form des Tetrahexaflexagon
von oben mit gleicher Nummerierung. Man verfährt entsprechend weiter.
Hexahexaflexagon (sehr bekannt)
top


1/236/2/315/3/124/ :||
Legt man die Dreiecke mit den Nummern 6 aufeinander, so erhält
man die Form des Pentahexaflexagon von oben mit gleicher Nummerierung.
Man verfährt entsprechend weiter.
Hexahexaflexagon (Variation B)
123/14/3/125/16/5/ :||
|
Hexahexaflexagon (Variation C)
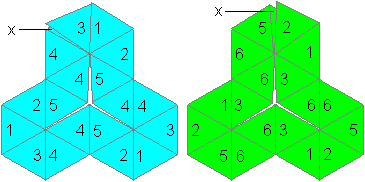
1256/2/51/23/14/3 :||
|
Eine ausführliche Beschreibung
dieses Flexagons findet man in meiner Seite Hexahexaflexagon.
Heptahexaflexagon


1367/3/61/324/3 :||
Legt man die Dreiecke mit den Nummern 7 aufeinander, so erhält
man die Form des linearen Hexahexaflexagons (Variation A) von oben mit
gleicher Nummerierung. Man verfährt entsprechend weiter.
Heptahexaflexagon
(Variation B)


1257/2/516/5/123/14/3/ :||
Legt man die Dreiecke mit den Nummern 7 aufeinander, so erhält
man die Form des Hexahexaflexagons (Variation B) von oben mit gleicher
Nummerierung. Man verfährt entsprechend weiter.
Tetraflexagons top
Es gibt auch Flexagons in Quadratform. Das folgende Tritetraflexagon
stammt aus Gardeners Buch von 1961, das Tetratetraflexagon aus David Mitchells
empfehlenswertem Bastelheft (4).
Ein Tritetraflexagon
... ... ... |
Zum Bau legt man nacheinander die Quadrate 3 und 3, 2
auf 2 und 1 und 1 aufeinander. Die Quadrate mit den Kreuzen werden aufeinander
geklebt. |
Ein Tetratetraflexagon
...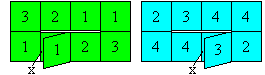 ... ... |
Hier faltet man zuerst 4 auf 4, dann folgen der Reihe
nach die nächsten Nummern.
Die Mitte ist horizontal über zwei Quadrate eingeschnitten,
die Quadrate mit x liegen am Ende. Das wird in der Zeichnung verdeckt. |
Öffnen
... ... ... |
Man findet normalerweise neue Flächen der Tetraflexagons,
indem man sie umdreht und dann wie ein Buch in der Mitte öffnet. |
Mehr findet man auf meinen Seiten Tetraflexagon
und Hexahexaflexagon.
Flexagons im Internet
top
Deutsch
Claus Michael Ringel
Flexagone
Randolf Rehfeld
Flexagone
Wikipedia
Flexagon
Englisch
Antonio Carlos M. de Queiroz
Hexaflexagons
Dave Richeson
Rubik’s
Cube Tri-Hexaflexagon
David King
Flexagons
Douglas C. George
Flexagon
Ela Schwartz
Flexagon
Fever
Eric W. Weisstein
Flexagon
Erik Demaine
Flexagon
Infinity12
Hexaflexagons
Jill Britton
Foto-TriHexaFlexagon
(THF) (Description of Fernando G. Sörensen's program, program
available)
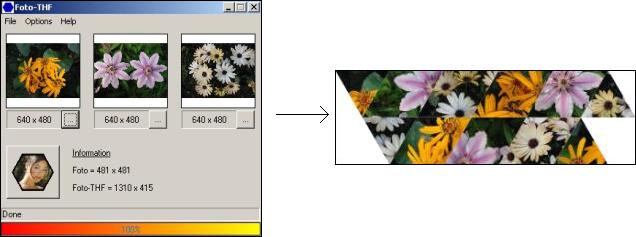
Program Foto-THF 1.2 (198Kb - fthf12.zip)
Choose "Opciones/Idioma/English (USA)"!
Kathryn Huxtable's
Flexagon
Page
Vi Hart (Khan Academy page)
Hexaflexagons
Kjartan Poskitt
The
Fabulous Flexagons
Les Pook
Flexagons
Martin Gardner
Hexaflexagons
Cambridge University Press, Martin Gardner’s First Book
of Mathematical Puzzles and Games (Excerpt)
Lee Stemkoski (Mathematrix)
Flexagons
NN
Flexifier
(Make your own tetra-tetraflexagon.)
Peter Bradshaw
Flexagon
Creator!
Robin Moseley
The Flexagon Portal
Scott Sherman
Flexagons |
Scott Sherman bietet viele Variationen von Flexagonen
aus Dreiecken an.
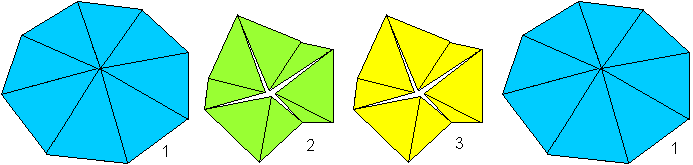
Dieses ist das "3 sided isosceles octaflexagon" (Tri-oktaflexagon)
als ein Beispiel.
Wenn man es in der Mitte öffnet, muss man wissen,
dass das Achteck in 2/3 der Stellungen nicht eben liegt. |
Wikipedia
Flexagon
www.g4g-com.org
Hexaflexagon
Youtube
Flexagon,
hexaflexagon-2
...
Yutaka Nishiyama
GENERAL
SOLUTION FOR MULTIPLE FOLDINGS OF HEXAFLEXAGONS (.pdf file)
Referenzen top
(1) Martin Gardner: Mathematical Puzzles & Diversions,
New York 1959
(2) Martin Gardner: The Second Scientific American Book
of Mathematical Puzzles & Diversions, New York 1961
(3) Martin Gardner: Mathematische Denkspiele, München
1987 [ISBN 3 88034 323 3]
(4) David Mitchell: The Magic of Flexagons, Norfolk England
1998 [ISBN 1 899618287]
(5) Les Pook: Flexagons Inside Out, Cambridge University
Press, 2003[ISBN 0 521 52574 8 paperback]
(6) Joseph S. Madachy: Madachy's Mathematical Recreations,
Dover Publications Inc., 1979
(7) Les Pook: Serious Fun with Flexagons, Springer-Verlag
GmbH, 2009 [ISBN-10: 9048125022], {106,95€}
Kommentar top
Arthur H. Stone erfand die Flexagons im Herbst 1939.
Flexagons wurden bekannt, nachdem Martin Gardner sie in
der Mathematik-Ecke des Magazins Scientific American Ende der 50er
Jahre vorstellte.
In dem Buch (1) von 1959 zieht der Autor auf 14 Seiten
Bilanz: Er bekam mehr als 100 Zuschriften.
Buch 3 enthält eine Anleitung zum Bau eines Hexatetraflexagons.
Es ist erstaunlich, dass Flexagons im deutschen Sprachbereich
kaum bekannt sind. Vielleicht liegt das auch daran, dass das oben genannte
erste Buch von Gardner zwar ins Deutsche übersetzt wurde, dass aber
das Kapitel über Flexagons fehlte.
Es ist kein Zufall, dass Flexagone an der ersten Stelle
meiner Homepage stehen. Ich kenne kaum eine andere mathematische Bastelei
dieser Qualität. Viel Spaß.
Hier noch ein Hinweis auf "räumliche Flexagone",
die Kaleidozyklen. Sie sind auch schön.
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |
|