|
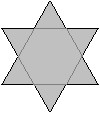
Was ist ein Stern?
... ... ...
|
Auf dieser Webseite findet man eine persönliche
Auswahl von Sternen.
Der linke Stern ist ein regelmäßiges Sechseck,
auf dessen Seiten sechs gleichseitige Dreiecke sitzen.
In diesem Sinne ist ein Stern allgemeiner eine Figur,
die aus einem konvexem Vieleck besteht, auf dessen Seiten Dreiecke gesetzt
werden. - Die Dreiecke heißen Zacken. |
Erzeugung von Sternen
top
Es gibt unterschiedliche Möglichkeiten Sterne zu
erzeugen.
1.Möglichkeit:
Man gibt ein regelmäßiges Vieleck vor und
setzt auf die Seiten gleichseitige Dreiecke.
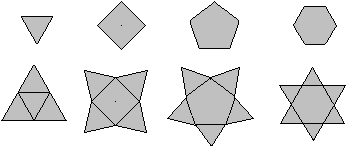
Diese Prozedur führt bei einem Dreieck als Ausgangsfigur
nicht zu einem Stern.
2. Möglichkeit:
Man gibt ein regelmäßiges Vieleck vor und
spiegelt die Grunddreiecke der Vielecke an einer Seite.
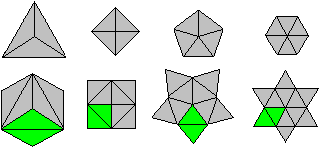 Diese Prozedur führt bei Drei- und Vierecken nicht zu
Sternen.
Diese Prozedur führt bei Drei- und Vierecken nicht zu
Sternen.
3. Möglichkeit:
Man gibt ein regelmäßiges Vieleck mit n Ecken
vor und dreht es um 180/n. Ursprung und Bild bilden zusammen einen Stern.
4. Möglichkeit:
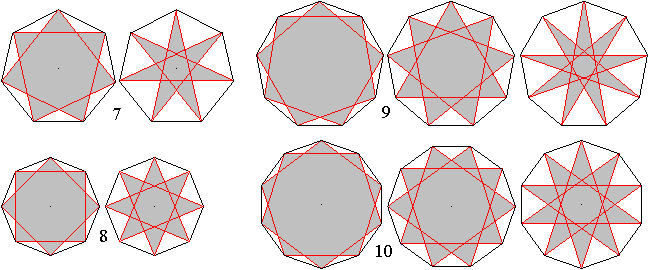
Man gibt ein Vieleck vor und zeichnet bestimmte Diagonalen.
Sie bilden dann Sterne. Speziell regelmäßige Vielecke führen
zu Sternen mit vielfältiger Symmetrie. Das Pentagramm und das Hexagramm
unten sind Beispiele.
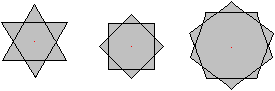
5. Möglichkeit:
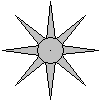
Man gibt ein regelmäßiges Vieleck vor und
setzt auf die Seiten gleichschenklige Dreiecke, die eine große Höhe
verglichen mit der Grundseite haben. Das Vieleck, das die Zacken trägt,
kann auch zu einem Kreis ausarten (ganz rechts).
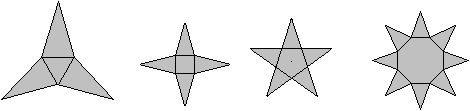 ................ ................
Es entstehen ansehnliche Sterne. Man erwartet offenbar, dass
Sterne spitze Zacken haben.
6. Möglichkeit:
Man gibt ein beliebiges Vieleck vor und setzt auf die
Seiten beliebige Dreiecke.
... ... ...
|
Dieser Stern ist dem Logo der Zeitschrift "Stern" nachempfunden. |
 HMATISSE
HMATISSE
Basteln von Sternen
top
Der Stern ist für den Bastler
ein beliebtes Thema mit einer Unzahl von Variationen.
Scherenschnitt

Der erste achtzackige
Stern entsteht durch einen Scherenschnitt.
...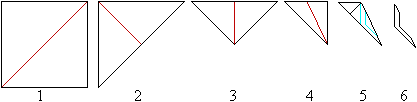 ... ... |
Man faltet ein quadratisches Blatt Papier immer wieder
längs der roten Linie, bis Bild 5 entsteht. Dann schneidet man Stücke
längs der blauen Linien mit einer kräftigen Küchenschere
ab. Es entsteht Bild 6. Durch Entfalten ergibt sich der Stern. |
Dieser Stern kann vielfältig abgewandelt werden. Man
schneidet nicht einfach einen Keil heraus, sondern wählt andere Formen
oder lässt Stege stehen.
Man kann auch schwarzes Tonpapier verwenden und die Öffnungen
mit farbigem Seidenpapier schließen. Dann entstehen Fensterbilder.
Aus Butterbrottüten
Diese einfachen, sternförmigen Faltarbeiten entstehen
aus jeweils acht Butterbrottüten.
Man findet im Internet Anleitungen mit "butterbrottüten
sterne basteln".

Meine Versuche mit acht Tüten
|

Tonys Stern aus sechs Tüten.
|
Origami-Blüten
... |
Hannah bastelte nach einer Anleitung bei besserbasteln.de
(URL unten)
die schönen Blüten.
Hannah, danke für den Hinweis. |
Fadenspiel
Polygramme top
Über die Hauptseite gelangt man zu den Webseiten
mit den Namen Pentagramm, Hexagramm,
Heptagramm
, Oktagramm und Nonagramm.
Das sind regelmäßige Sterne, die man erhält,
wenn man wie oben in regelmäßige Vielecke Diagonalen einzeichnet.
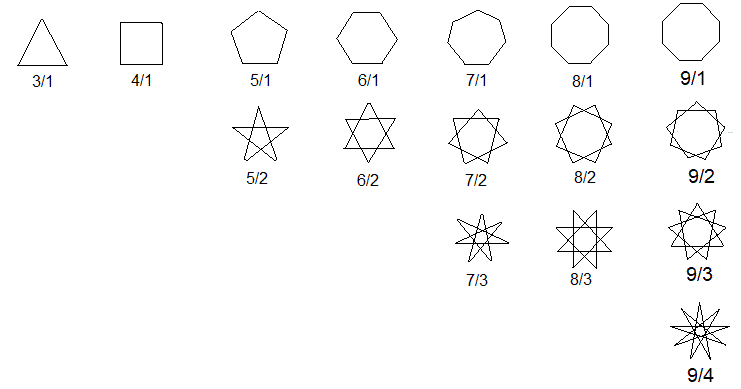
Zwei Quilts top


Sterne fern und nah
top
fern
Viele Nationen haben in ihren Nationalflaggen einen oder
mehrere Sterne. Hier ist eine kleine Auswahl:

nah
In Lippe gibt es noch viele Fachwerkhäuser mit einem
großen Deelentor, durch das früher ein Pferdewagen in das Haus
fahren konnte. Über dem Tor befindet sich im allgemeinen eine Hausinschrift,
seitlich daneben oder darunter der Stern von Burg Sternberg (hier siebenzackig)
und auf der anderen Seite die sternförmige lippische Rose.
 .......... .......... Oben als ein Beispiel ein Haus auf Gut Hovedissen in Leopoldshöhe,
Kreis Lippe.
Oben als ein Beispiel ein Haus auf Gut Hovedissen in Leopoldshöhe,
Kreis Lippe.
Ein Unikum befindet sich im Stadtwappen der Stadt Barntrup
in Lippe (rechts). "Der halbe Stern erinnert an die Gründung der Stadt
durch die Grafen zu Sternberg. Die halbe lippische Rose wurde von der Stadt
nach dem Übergang der Grafschaft Sternberg an die Herrschaft Lippe
in das städtische Siegel übernommen."
Quelle: http://www.lippe.de/new/allgemein/show.php3?s=3&n=wappen
Stern und Rose findet man auch am historischen
Rathaus von 1546 meiner Heimatstadt Bad Salzuflen.
 ......... .........
... ... ... |
Die lippische Rose befindet sich übrigens
auf der Flagge des Landes Nordrhein-Westfalen.
Sie ist ein Hinweis auf die Eingliederung des Landes Lippe
an NRW nach dem zweiten Weltkrieg. |
Sterne
an anderen Stellen meiner Homepage top
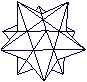
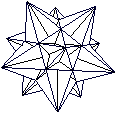
Kepler-Poinsot-Körper
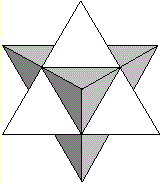
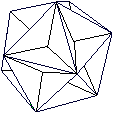
Oktaederstern
Gefalteter
Sterne
Sterne im Internet
top
Deutsch
HERRNHUTER STERNE GMBH
Bauanleitungen
für Herrnhuter Sterne
Joachim Mohr
Die stetige Teilung
oder der goldene Schnitt und die Konstruktion des regelmäßigen
Fünfecks
Lena Pauline Hönisch Jurado (besserbasteln.de)
Videoanleitung:
Spitze Fleurogami Blüte falten
origamiseiten.de
Bildergalerie
nachgefalteter Modelle (Sterne)
Wikipedia
Stern
(Geometrie), Unikursales_Hexagramm
Englisch
BETSY ROSS
How
to Cut a 5-Pointed Star in One Snip
Eric W. Weisstein (World of Mathematics)
Star
Polygon,
Kepler-Poinsot
Solid
Wikipedia
Star
polygon
Referenzen top
(1) Martin Gardner: Mathematischer Zirkus, Berlin 1988
(ISBN 3550076924)
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |



 HMATISSE
HMATISSE

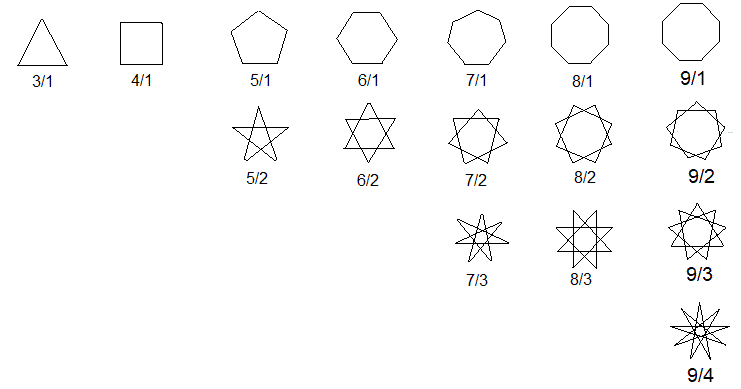

 ..........
..........
 .........
.........
 ...
...
 ................
................
 ...
... ...
...









 ...
...