|
Was ist der gefaltete Fünfeckstern?
... ... |
Auf der Suche im Internet nach einem Weihnachtsstern
bin ich auf diesen Stern in Form eines Pentagramms gestoßen. |
... ... |
Beim Basteln des Sterns geht man von einem quadratischen
Blatt Papier aus und stellt vorweg durch Falten und Schneiden ein regelmäßiges
Fünfeck her.
Aus dem Fünfeck entsteht dann der Stern. |
Erster Schritt:
Das Fünfeck top
1
... |
Gehe also von einem quadratischen Blatt Papier aus.
 |
2
... |
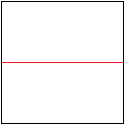Falte es an der Mittellienie.
|
3
... |
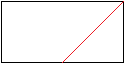Falte diagonal wie in der Zeichnung angegeben und entfalte
wieder.
|
4
... |
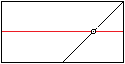Falte an der Mittellinie und entfalte wieder.
Es kommt nur auf den Schnittpunkt der beiden Faltlinien
an. Deshalb genügt es, die beiden Faltlinien so weit auszuführen,
dass man ihn erkennt. - Markiere ihn.
|
5
... |
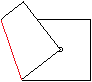Falte so, dass die linke untere Ecke den Schnittpunkt
berührt.
|
6
... |
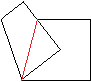Falte an der roten Linie.
|
7
... |
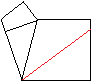Falte an der roten Linie.
|
8
... |
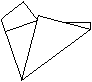Das müsste dann so aussehen.
|
9
... |
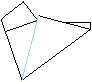Falte an der blauen Linie als Bergfaltung.
|
10
... |
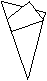Das müsste dann so aussehen.
|
11
... |
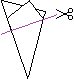Schneide längs der violetten Linie den oberen Teil
ab.
|
12
... |
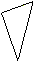Das müsste dann so aussehen. |
13
.. . |
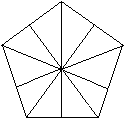Entfalte das Dreieck; es ist ein regelmäßiges
Fünfeck entstanden.
|
... |
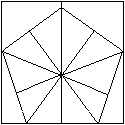So liegt das Fünfeck im Quadrat.
Durch die Faltungen ist der Vollwinkel 360° in 10
gleiche Winkel aufgeteilt.
So entsteht mit 72° der Mittelpunktswinkel eines
Fünfecks. |
Zweiter
Schritt: Vom Fünfeck zum Stern top
Ich verzichte auf eine Anleitung durch Zeichnungen und
verweise auf Videos bei Youtube (URL unten).
... ... |
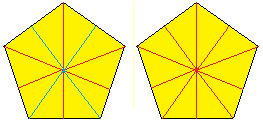
Das ist die Rückseite des Sterns.
Ich zeige das Bild, weil ich beim Herunterdrücken
der Zacken zuerst Schwierigkeiten hatte, dabei das weiße Fünfeck
zu erzeugen. Da sollte man Geduld haben und erst die Zacken in die Ebene
legen, bis sich das kleine Fünfeck fast von selbst ergibt.
Das ist leichter, wenn man zu Beginn alle Faltungen zu
Talfaltungen macht.
|
Man braucht übrigens 22 Faltungen, um den Stern fertig
zu stellen.
Etwas Mathematik
top
... |
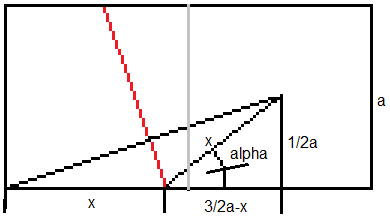Es gilt nach dem Satz des Pythagoras x² = (3/2a-x)²+(1/2a)².
Daraus folgt x=5/6a.
Es gilt sin(alpha) = (1/2a)/x = 0,6. Daraus folgt gerundet
alpha = 36,87°.
Für ein regelmäßiges Fünfeck müsste
alpha = 36° sein. |
Ergebnis: Durch die Faltungen entsteht näherungsweise
ein regelmäßiges Fünfeck bzw. Pentagramm.
Der kleine Unterschied von 0,87° macht sich beim
Falten nicht bemerkbar.
Es ist möglich, (umständlicher) ein echtes
regelmäßiges Fünfeck zu falten, siehe unten.
Hinweis:
... ... |
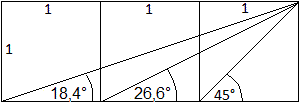In der Zeichnung oben taucht mit dem Dreieck mit den
Katheten 1/2a und 3/2a die Figur des Drei-Quadrate-Satzes auf. Der Satz
besagt, dass die beiden Winkel links zusammen so groß sind wie der
Winkel rechts. Den Beweis findet man auf meiner Seite 3_4_5_Dreieck. |
Verschiedenes
top
Hannahs Sterne
Ein Fünfeck durch
Flechten
Auf meiner Seite Nur ein Streifen
Papier zeige ich, wie man mit einem Knoten eines Papierstreifens ein
Fünfeck erzeugt.
Links
zum Fünfeck und zum Fünfeckstern top
Links zum Fünfeckstern oben
HG Homemade Gifts Made Easy
How
to Cut a Pentagon From a Square
HG Homemade Gifts Made Easy
Folding
a 5 Pointed Origami Star
Ich empfehle die beiden Videos in englischer Sprache,
die man stumm schalten kann.
NN
Sterne
basteln - Origami Sterne falten
Vom Quadrat zum Stern - Musik unterlegt
Origami
Sterne basteln - Einfache Anleitung zum Falten für Weihnachten | TRYTRYTRY
Video in deutscher Sprache
Regelmäßiges Fünfeck
falten
... ... |
Es gibt auch die Möglichkeit, ein regelmäßiges
Fünfeck im Quadrat exakt zu falten.
Das Fünfeck entsteht nach 13 Faltungen.
Auf der folgenden Webseite findet man ein Anleitung und
etwas Mathematik dazu.
Link: Laszlo C Bardos Fold
a Regular Pentagon
Weiteter Link: Mathematikus Falten
eines Fünfecks |
| ...... |
Zum Vergleich:
Oben ergibt sich das Fünfeck schon nach sechs Faltungen
und einem Schnitt. Praktisch: Die Faltlinien benötigt man weiter für
den Stern. |
Fünfeck aus einem
A4 Blatt
 |
Bei einem A4-Blatt beträgt der Winkel alpha zwischen
der Diagonale und der kleineren Seite gerundet 54,7°.
Durch vier Tal-Faltungen in der Reihenfolge 1, 2, 3,
4 erzeugt man ein Fünfeck.
Bei einem regelmäßige Fünfeck beträgt
der Winkel an der Spitze 104° und alpha wäre 52°.
Ergebnis: Das gefaltete Fünfeck ist fast regelmäßig.
Die Abweichung beträgt nur 2,7°. |
Quelle: How
to fold PENTAGON from A4 (Video)
Weiterer Link: Folded
Pentagon
Weitere Links
deschdanja
5
zackiger Stern
Diana Todt
Falten
eines regelmäßigen Fünfecks (pdf-Datei)
schaeresteipapier
Origami
Stern (Youtube)
cut-the-knot.org
Regular
Pentagon Inscribed in Circle by Paper Folding
David Dureisseix (Institut National des Sciences Appliquées
de Lyon)
Folding
optimal polygons from squares
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
http://www.mathematische-basteleien.de/
© Dezember 2022 Jürgen
Köller
top |
