Was sind die Kepler-Poinsot-Körper?
Dazu kommen noch vier nichtkonvexe Körper, die Kepler-Poinsot-Körper:
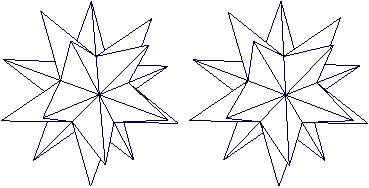
Auf dieser Seite werden die vier Körper der Reihe nach besprochen. Die folgenden Bildpaare auf dieser Seite ermöglichen eine räumliche Sicht der Körper. Kleines
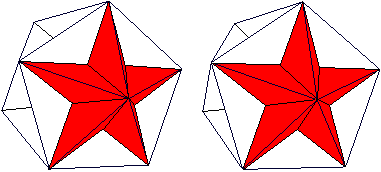
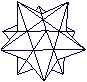
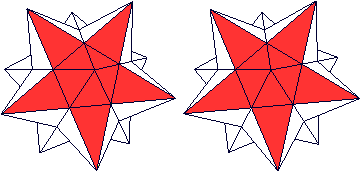
Sterndodekaeder top
 Auf seine Seitenflächen werden gerade, fünfseitige Pyramiden gesetzt.
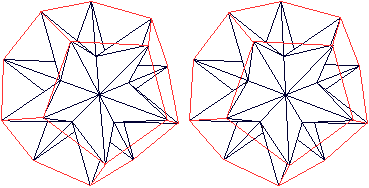
Es entsteht ein dreidimensionaler Stern mit 12 Zacken,
von denen hier 11 zu sehen sind.
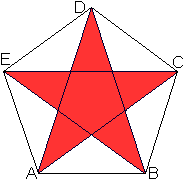
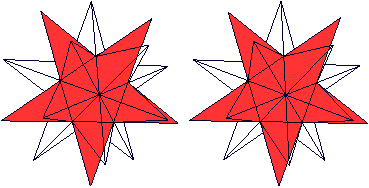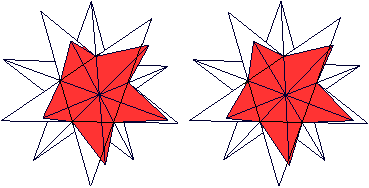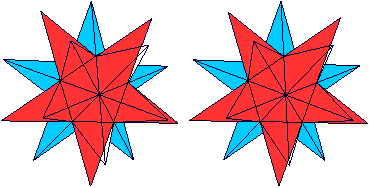
Durchsichtig 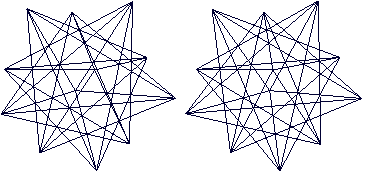 Man erkennt vielleicht im Zentrum das Dodekaeder. Die 12 Fünfecke des Pentagondodekaeders sind Teil eines fünfzackigen, ebenen Sterns. Im folgenden Bild wird ein "Pentagramm" markiert.
Neben den 12 Seitenflächen hat das Sterndodekaeder noch 30 Kanten und 12 Ecken. Betrachtet man die gleichschenkligen Dreiecke des Pentagramms, so gibt es 60 Flächen, 90 Kanten und 32 Ecken. Verbindet man die Spitzen der Zacken miteinander, entsteht ein Ikosaeder. 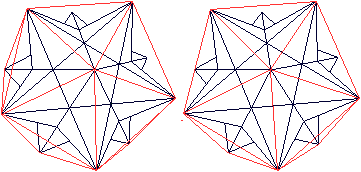 Das ist deshalb nicht weiter erstaunlich, weil das Ikosaeder der duale Körper des Pentagondodekaeders ist. 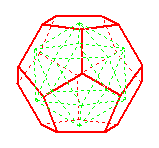
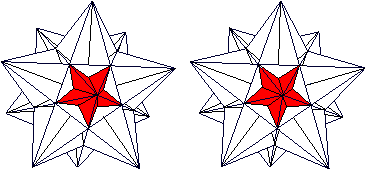
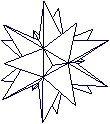
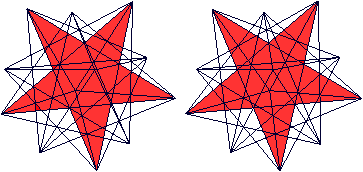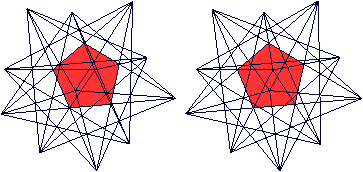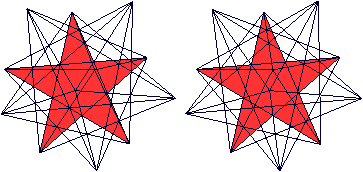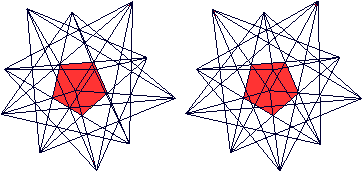
Großes
Sterndodekaeder top
Auf seine Seitenflächen werden gerade, dreiseitige Pyramiden gesetzt.
Es entsteht ein dreidimensionaler Stern mit 20 Zacken,
von denen hier 15 zu sehen sind.
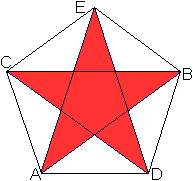
Durchsichtig 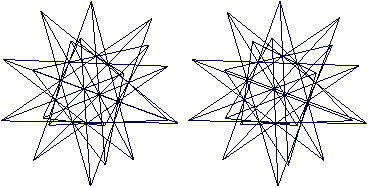 Man erkennt vielleicht im Zentrum das Ikosaeder. Im folgenden Bild wird ein Pentagramm rot markiert.
Dann gibt es noch zehn Pentagramme, deren Spitzen vorne
eine fünfzackige Krone bilden.
Man kann im Körper also auch 12 Pentagramme ausmachen.
In diesem Sinne ist auch das Große
Sterndodekaeder
ein regelmäßiger Körper aus
12 Pentagrammen.
Neben den 12 Seitenflächen hat es noch 30 Kanten und 20 Ecken. Verbindet man die Spitzen der Zacken miteinander, entsteht ein Pentagondodekaeder.
Das ist deshalb nicht weiter erstaunlich, weil das Pentagondodekaeders der duale Körper des Ikosaeder ist. 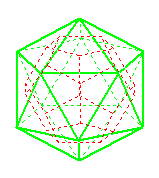
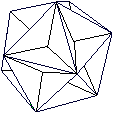
Großes Dodekaeder top
Das ist eine Ansicht des großen Dodekaeders.
Es hat die Grundform eines Ikosaeders, dessen Dreiecke Vertiefungen in Form von flachen Dreieckspyramiden haben. Hier ist eine Pyramide eingezeichnet. 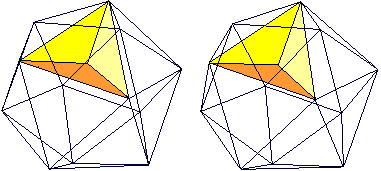 Mit allen Vertiefungen erkennt man ein Fünfeck mit einem erhabenen Stern aus fünf Rippen.
Das Augenmerk soll auf die Fünfecke gerichtet werden, auf denen die Sterne sitzen. 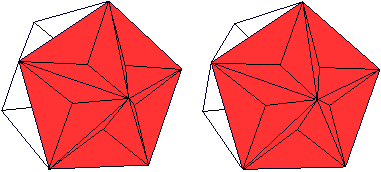 Es gibt 12 Fünfecke. 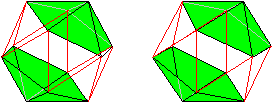 Dazu muss man wissen, dass ein Ikosaeder auch ein Antiprisma ist. Zu je zwei gegenüberliegenden Ecken gibt es immer zwei Fünfecke als Grundfläche von Fünfeckspyramiden. Da das Ikosaeder sechs Paare gegenüberliegender Ecken hat, kommt man auf insgesamt 12 Fünfecke. Diese Fünfecke sind regelmäßig und durchdringen
sich. Sie bilden das konkave Große Dodekaeder.
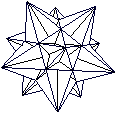
Neben den 12 Seitenflächen hat es noch 30 Kanten und 12 Ecken. Betrachtet man die gleichschenkligen Dreiecke, so gibt es 60 Flächen, 90 Kanten und 32 Ecken. Großes Ikosaeder
top
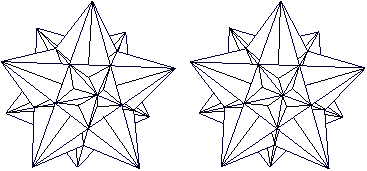 Er hat die Grundform des Kleinen Sterndodekaeders, des ersten Körpers auf dieser Seite. Hier ist er noch einmal. 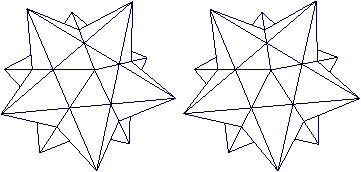 Die äußeren Dreiecke erhalten Vertiefungen in Form von flachen Dreieckspyramiden. Hier ist eine Pyramide eingezeichnet. 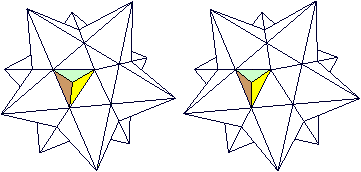 Mit allen Vertiefungen erkennt man, dass ein Zacken in Form einer fünfseitigen Pyramide durch einen erhabenen Stern aus fünf Rippen ersetzt wird.
Das Augenmerk soll auf gleichseitige Dreiecke im Körper gerichtet werden. Dazu dreht man den Körper. 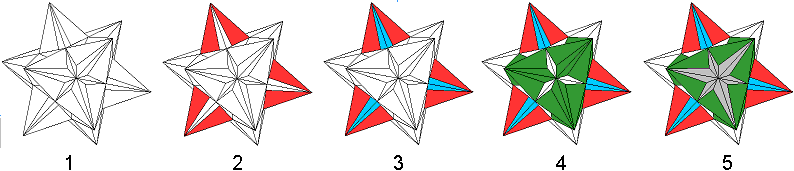 (3) Auf dem Dreieck liegen drei Rippen (blau). (4) In der Mitte liegen drei Zacken aus Rippen (grün). Sie liegen so, dass die Spitzen ein (fast) gleichseitiges Dreieck bilden. (5) Zentral liegen sechs Rippen (grau). Es ist jetzt möglich, die Dreiecke zu zählen:
Neben den 20 Seitenflächen hat es noch 30 Kanten und 12 Ecken. Zusammenfassung top
Sie sind kugelförmig, und an jeder Ecke treffen sie in gleicher Weise aufeinander. So erfüllen sie die Bedingungen eines regelmäßigen Körpers. Es gibt nur 5+4 Körper dieser Art. Die regelmäßigen Vielecke erkennt man gut in den folgenden farbigen Bildern des Programms Small Stella. Vom Programm aus kann man die Körper mit der Maus auch noch drehen.
Kepler-Poinsot-Körper im Internet top Deutsch H.B.Meyer (Polyeder aus Flechtstreifen)
Holger Ullmann (TETRAKTYS)
Wikipedia
Englisch H.B.Meyer (Polyeder aus Flechtstreifen)
Herman SERRAS
Eric.W.Weisstein
Fortran friends
George W. Hart
G. Korthals Altes
Robert Webb
Wikipedia
Referenzen top
URL meiner
Homepage:
© 2008 Jürgen Köller |

 ...
... ...
...
 ...
...