|
Was ist ein Oktagramm?
...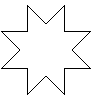 |
Ein Oktagramm ist ein regelmäßiger Stern mit
acht Zacken. |
Entstehung
...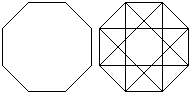 ... ... |
Der Stern entsteht, indem man die Eckpunkte des Achtecks
so verbindet, dass man jeweils drei Punkte überspringt. Dabei entsteht
eine geschlossene Linie.
Die Seiten des Sterns sind die mittleren Diagonalen des
Achtecks. |
Stern
von Lakshimi
... |
 ... ... |
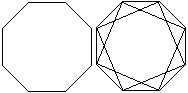
Neben dem Oktagramm gibt es noch einen zweiten regelmäßigen
Stern.
Der Stern entsteht, indem man jeden zweiten Punkt des
Achtecks verbindet.
Es besteht aus zwei Quadraten. |
Das zusammengesetzte Oktagramm wird von den kurzen Diagonalen
gebildet.
Unregelmäßiges
Oktagramm
... ... ... |
Wenn man vom Wort her kommt, müsste man auch den
nebenstehenden Stern als Oktagramm bezeichnen, denn Oktagramm heißt
"mit acht Strichen". |
Achtzackstern
... ... ... |
Ein allgemeinerer achtzackiger Stern entsteht, wenn man
auf ein konvexes Achteck beliebige Dreiecke setzt. Diesen Stern sollte
man nicht mehr als Oktagramm bezeichnen. Er besteht nicht aus acht, sondern
aus 24 Strichen oder Strecken.
Er könnte achteckiger Stern, Achtzackstern, Achteckstern
oder Achtstern heißen. |
Einordnung
...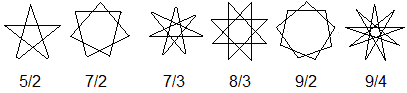 ... ... |
Das Oktagramm gehört zu den Polygrammen,
die durch Brüche gekennzeichnet werden. |
Die erste Zahl gibt die Anzahl der
Eckpunkte des erzeugenden Vielecks an, die zweite die "Sprungweite" beim
Verbinden der Eckpunkte.
 |
Der Stern von Lakshimi 8/2 ist
ein zusammengesetztes Polygramm und besteht aus zwei Quadraten. |
Erweiterung
Die beiden unregelmäßigen Sterne sind nahe
liegende Verallgemeinerungen des regelmäßigen Sterns. Sie sind
aber nicht relevant.
Mehr dazu auf meiner Seite Polygramm.
Spielereien top
Rauten
...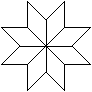 |
Gibt man acht 45°-Rauten vor, so kann man aus ihnen
ein Oktagramm bilden. |
Räumlich
...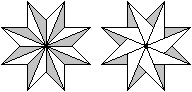 |
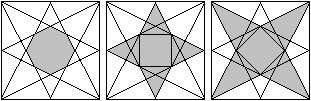
Zeichnet man die langen Diagonalen und färbt Dreiecke,
so erscheint die Sterne räumlich.
Auch mit Teilabschnitten der Diagonalen entstehen ansehnliche
Sterne. |
Keltischer
Knoten
... ... ... |
Zeichnet man die Linien des Oktagramms dicker und dann
abwechselnd Brücken und Unterführungen, so entsteht ein geflochtener
Stern. |
Stern
im Stern
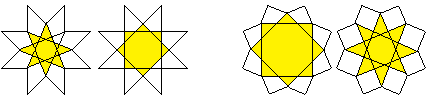
Linien
im Achteck und im Oktagramm
...
...
.. 
..
Kopiert
aus meiner Webseite Regelmäßiges Achteck
Parkettierungen
... |

Fliese aus Sevilla...................... |
 |
 Schülerarbeit, 10 Jahre, 1950
Schülerarbeit, 10 Jahre, 1950
|
Mehr au meiner Seite Begegnungen mit
Parkettierungen
Überschlagene
regelmäßige Achtecke top
...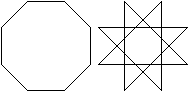 ... ... |
Das Oktagramm kann man auch als ein regelmäßiges
Achteck ansehen, bei dem die acht Eckpunkte durch Linien verbunden werden,
die sich überschneiden. |
Es gibt noch weitere überschlagene
Achtecke, darunter sind bizarre Figuren.
...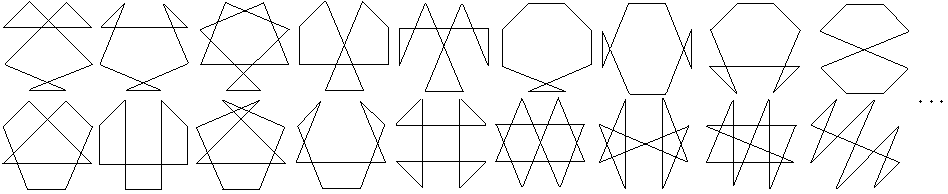
Es stellt sich die Frage,
wie viele überschlagene Achtecke es gibt.
Sie sind Hamiltonkreise,
da die Punkte durch eine geschlossene Linie verbunden werden.
Stern von Lakshmi top
... |
Das ist der zweite Stern im Achteck. Seine Zacken sind
kürzer. |
"Der Stern von Lakshimi wird
im Hinduismus verwendet, um Ashta-lakshmi, die acht Formen des Reichtums
zu symbolisieren."
[Quelle: https://mathworld.wolfram.com/StarofLakshmi.html]
Entstehung
...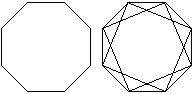 |
Er entsteht, indem man in ein regelmäßiges
Achteck die kurzen Diagonalen einzeichnet. |
... ... ... |
Er entsteht auch, indem man zwei Quadrate übereinander
legt und dann ein Quadrat um den gemeinsamen Mittelpunkt um 45° dreht. |
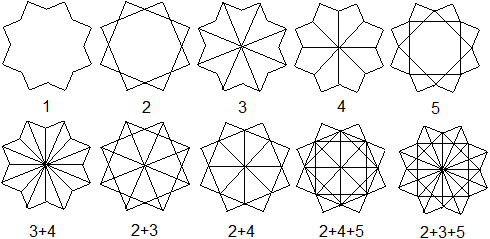
Linien
im Stern von Lakshmi
...
Formeln top
Auf meiner Seite Polygramm werden Formeln für den
p/q-Stern hergeleitet.
In diesem Kapitel geht es um Formeln für die beiden
Oktagramme, den 8/2-Stern und den 8/3-Ster.
An einem Heptagramm werden
bekannte Größen eines Polygramms angezeigt.
...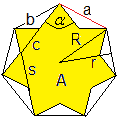 |
alpha - Winkel an der Spitze
s - Seitenlänge
c - Grundseite einer Zacke
b - Schenkel einer Zacke |
R - Radius des Umkreises
r - Radius des Inkreises
A - Flächeninhalt des Sterns
a - Seitenlänge des umfassenden Fünfecks |
Wenn die Seite a des umfassenden
Vielecks oder Polygons gegeben ist, so gelten für den p/q-Stern die
folgenden Formeln.
Winkel an der Spitze alpha
Seitenlänge s
Grundseite einer Zacke c
Schenkel einer Zacke b
Radius des Umkreises R
Radius des Inkreises r
Flächeninhalt des Sterns A |
alpha = [(p-2q)/p]*180°
s = a*sin(180°q/p)/sin(180°/p)
c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}
b = (a/2)/{cos[(q-1)/p]*180°}
R = (a/2)/sin(180°/p)
r = (a/2)/tan(180°/p)
A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa² |
Oktagramm
8/2
...
Für den 8/2-Stern, also für p=8 und q=2 gilt:
| Winkel an der Spitze alpha = [(p-2q)/p]*180° = (1/2)*180°
= 90°
Seitenlänge s = a*sin(180°q/p)/sin(180°/p)
= a*sin 45°/sin 22,5° = a*(1/2)sqrt(2)/{sqrt[2-sqrt(2)]/2}
= ... = sqrt[2+sqrt(2)]a
Grundseite einer Zacke c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180
°}= a*sin 45°/cos 22,5° = sqrt[2-sqrt(2)]
Schenkel einer Zacke b = (a/2)/{cos[(q-1)/p]*180°}
= (a/2)/cos 22,5° = (1/2)sqrt[4-2sqrt(2)]
Radius des Umkreises R = (a/2)/sin(180°/p)
= (a/2)/sin 22,5° = (1/2)sqrt[4+2sqrt(2)]
Radius des Inkreises r = r = (a/2)/tan(180°/p)
= (a/2)/tan 22,5° = (1/2)[sqrt(2)+1]
Flächeninhalt A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa²
= 2a²(1/tan 22,5°-tan 22.5°) = 4 |
.
.Gerundete
Werte
.
.s = 1,85a ...........
.
.c = 0,76a
.
.b = 0,54a
.
.R = 1,31a
.
.r = 1,21a
.
.A = 4a² |
Zusammengesetztes
Oktagramm 8/3
...
Für den 8/3-Stern, also für p=8 und q=3, gilt:
Winkel an der Spitze alpha = [(p-2q)/p]*180° =
(1/4)*180° = 45°
Seitenlänge s = a*sin(180°q/p)/sin(180°/p)
= a*sin 67,5°/sin 22,5° = ... = (1+sqrt(2)a
Grundseite einer Zacke c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}=
a*sin 22,5°/cos 45° = (1/2)sqrt[4-2sqrt(2)]
Schenkel einer Zacke b = (a/2)/{cos[(q-1)/p]*180°}
= (a/2/cos 45°) = ... = (1/2)sqrt(2)a
Radius des Umkreises R = (a/2)/sin(180°/p)
= (a/2)/sin 180°/8 = ... = (1/2)[sqrt(4+2sqrt(2)]a
Radius des Inkreises r = (a/2)/tan(180°/p) =
(a/2)/tan 180°/8 = (a/2)/tan 22,5° = (1/2)[sqrt(2)+1]a
Flächeninhalt A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa²
= 2*(1/tan 22,5°-tan 45°)a² = ... = 2sqrt(2)a² |
.
.Gerundete
Werte
.
.s = 2,41a
.
.c = 0,54a
.
.b = 0,71a
.
.R = 1,31a
.
.r = 1,21a
.
.A = 2,83a² |
Für die Berechnungen verwendet man u.a. sin 22,5°
= (1/2)sqrt[2-sqrt(2)], cos 22,5° = (1/2)sqrt[2+sqrt(2)] und tan 22,5°
= sqrt(2)-1.
Fünf Achtzacksterne
top
Eins
...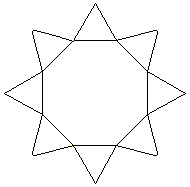 |
Es geht zuerst um Sterne, die entstehen, wenn man auf
ein regelmäßiges Achteck gleichseitige Dreiecke stellt. |
Antiprisma
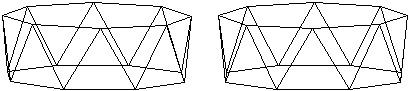
Das Antiprisma
besteht, wie der Grundriss zeigt, aus zwei regelmäßigen Achtecken
und 16 gleichseitigen Dreiecken.
Das Bildpaar ermöglicht eine
räumliche Sicht des Körpers.
... ... ... |
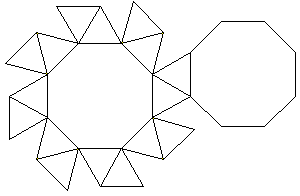 |
Ein Stern ergibt sich, wenn man acht Zacken nach oben bzw.
nach unten klappt.
Zwei
Abgeschrägtes quadratisches
Antiprisma
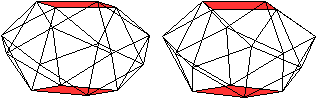
Das ist der Johnson-Körper
85. Zwischen zwei quadratischen Grundflächen liegt ein Geflecht aus
24 gleichseitigen Dreiecken.
Wird er parallel zu den Quadraten
projeziert, so erkennt man in der Parallelprojektion zwei Sterne.
Stereobild
|
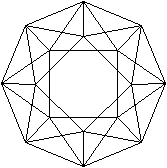
Parallelprojektion
|
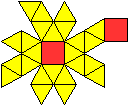
Grundriss
|
...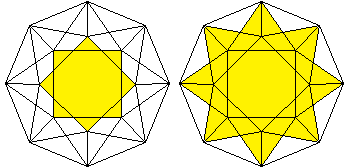 |
Die beiden Sterne sind gefärbt.
Links steht der Stern von Lakshmi, rechts ein Stern, der
dem Oktagramm nahe kommt. |
Drei
Regelmäßiger Stern
...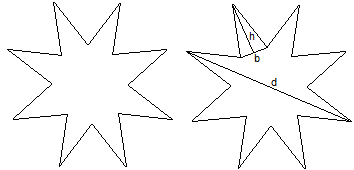 ... ... |
Das ist ein regelmäßiger
Stern, der entsteht, wenn man auf die Seiten eines regelmäßigen
Achtecks gleichschenklige Dreiecke setzt. Er wird durch drei Stücke
festgelegt, z.B. durch den Durchmesser d des Sterns, die Basis b der Zacke
und seine Höhe h.
Auf der Webseite Online-Rechner
(URL unten) heißt der Stern Doppelstern. Es kann sogar - noch allgemeiner
- jede zweite Zacke kürzer sein. |
...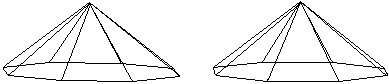 ... ... |
Wenn die Zacken hinreichend spitz sind, kann man sie
hochklappen und eine achtseitige Pyramide bilden............................................................... |
Vier
...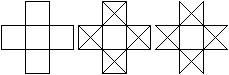 ... ... |
Zeichnet man in ein griechisches
Kreuz in die äußeren Quadrate die Diagonalen, so entsteht
ein achtzackiger Stern. . |
...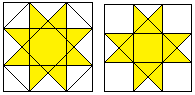 ... ... |
Auf den ersten Blick sieht er aus wie das Oktagramm.
Stellt man sie nebeneinander, erkennt man Unterschiede.
Die Flächeninhalte z.B. stehen im Verhältnis
[(1/2)*27*sqrt(2)-18]:1 oder ungefähr 1,09:1. |
Fünf
Ein Stern im Quadrat
...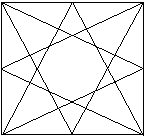 |
Ein Stern entsteht dadurch, das man die Eckpunkte eines
Quadrats mit den Seitenmitten verbindet. |
... ... ... |
Auf meiner Webseite Regelmäßiges
Achteck werden diese Figuren in einem Quadrat ausführlich besprochen. |
Origami top
Zwei
gefaltete Sterne Webseite
Regelmäßiges
Achteck
... ... ...
Achtstrahlige Blüte von David Collier,
gefaltet von Volker Sayn
|

Achtstrahliger Stern von Tomoko Fuse,
gefaltet von Volker Sayn
|
Blüten
mit acht Blütenblätter
... Scharbockskraut
Scharbockskraut
|
 Mädchenauge
Mädchenauge
|
 Clematis
Clematis
|
Von meiner Webseite Achtstrahlige
Figuren
Oktagramm im Internet
top
Deutsch
Online-Rechner
Oktagramm,
Stern
von Lakshmi,
Doppelter
Stern
Wikipedia ,
Stern
(Geometrie), Schläfli-Symbol,
Polygon
Englisch
Eric W. Weisstein (World of Mathematics)
Octagram,
Star
of Lakshmi,
Star
Polygon, Schlaefli
Symbol
Online-Rechner
Octagramm,
Star-of-Lakshmi,
Double-Star-Polygon
Wikipedia
Octagram,
Star
of Lakshmi,
Star
polygon
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
12/2023 Jürgen Köller
top |





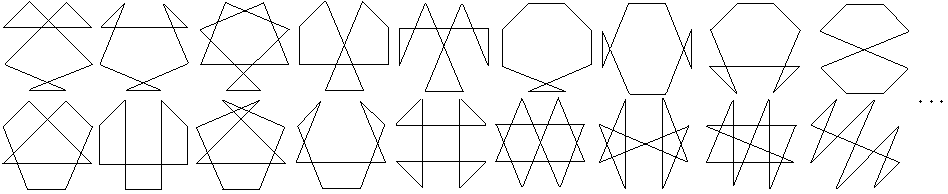



 ...
...
 ...
... ...
... ...
...


 ...
...



 ...
...
 ...
...

 ...
...




 ...
... ...
... ...
... ...
...
 ...
...
 ...
...



