|
Was ist "The Shinsei Miracle"?
... ... ... |
"The Shinsei Miracle" ist ein Puzzle in Würfelform.
Der Würfel ist außen goldfarben.
Er besteht aus 24 Dreieckspyramiden. Bestimmte Kanten
der Pyramiden sind miteinander verbunden. |
Der Würfel wird als edles Sammlerstück gehandelt
und kostet fast 100 $.
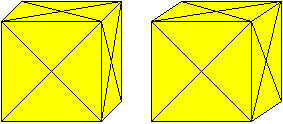
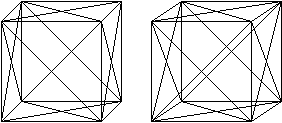
Wer den Stereoblick beherrscht, sieht die Doppelbilder
auf dieser Seite dreidimensional.
Der Würfel lässt sich leicht in zwei Hälften
zerlegen.
Beide Hälften greifen ineinander und bilden zusammen
den Würfel. Die gelbe Farbe soll die goldene Folie, mit der der Würfel
beklebt ist, darstellen. Grau bedeutet silbrig.
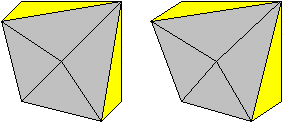
Das Besondere ist, dass man die beiden Hälften für
sich auseinander klappen kann und dass man dann zwei Ringe in Sternform
erhält (kein Stereobild!)
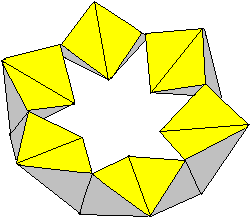 
Es sind viele andere Körper möglich, wie die
Fotos am Ende andeuten.
Der Würfel wurde von
Naoki Yoshimoto entwickelt.
Auf der beigelegten Beschreibung des Würfels steht
unter der Überschrift "Chains that make many wonderful shapes":
Made in Hongkong for Thomas Salter Ltd., Woodside Road,
Glenrothes, Fife ©1982.
Aufbau des Würfels
top
Der Würfel besteht wie gesagt aus 24 Pyramiden.
Begrenzungskanten der Pyramiden sind unter anderen alle Kanten und Flächendiagonalen
des Würfels, die von außen zu sehen sind.
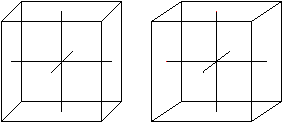
Für die Kanten innerhalb des halben Würfels
zeichnet man durch den Mittelpunkt die Parallelen zu den Seitenflächen
und die Raumdiagonalen ein.
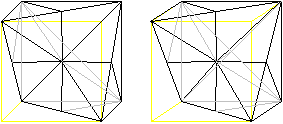
Man erkennt die Pyramiden besser, indem man die Grundflächen
dieser Dreieckspyramiden färbt und sich die Spitzen im Mittelpunkt
des Würfels nur denkt. Die Grundflächen sind halbe Quadrate,
und sie liegen auf der Oberfläche des Würfels.
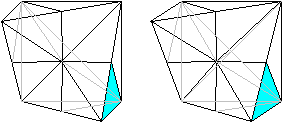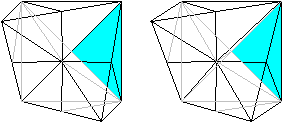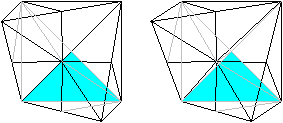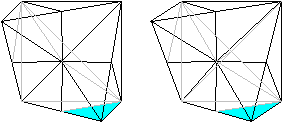
Sechs Pyramiden liegen an der Ecke unten, rechts, hinten.
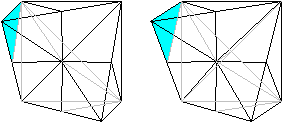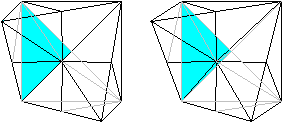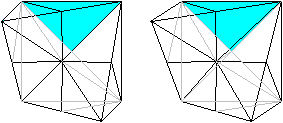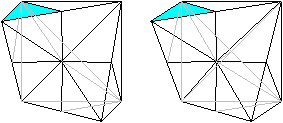
Sechs Pyramiden liegen an der Ecke oben, links, hinten.
Es wäre noch zu klären, wo die Dreieckspyramiden
miteinander verbunden sind.
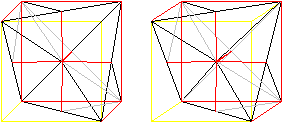
Die "Scharniere" sind rote Linien. - Zwei Scharniere von
der Mitte nach hinten fallen in der Zeichnung zusammen.
Daten einer Pyramide
top
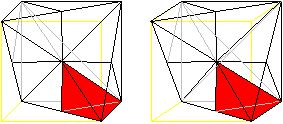
Es wird eine Dreieckspyramide herausgegriffen.
...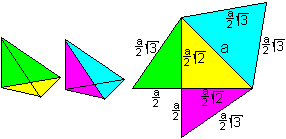 ... ... |
Mit Hilfe der Würfeldaten
Kantenlänge a, Flächendiagonale sqrt(2)a, Raumdiagonale
sqrt(3)a
erhält man die nebenstehenden Größen
der Pyramide.
Die Würfelkante sei a.
Betrachtet man das gelbe Dreieck als Grundfläche,
dann ist die Höhe der Pyramide a/2. Das ergibt ein Volumen von (a²/4)*(a/2)/3=a³/24.
Da es 24 Pyramiden im Würfel gibt, ergibt sich als
Probe das Würfelvolumen V=a³. |
...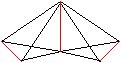 |
Die Dreieckspyramiden bilden eine Kette. Die Scharniere
sind rot gekennzeichnet.
Sechs Scharniere des Würfels haben die Länge
a, sechs die Länge a/2. |
Fotos top

Würfel
|

|

Sechs-Rauten-Körper
|

Ein halbes Rhombendodekaeder
|

|

|
Variante top
Ich stelle hier noch eine Variante vor, auf die Hans
Dybkjær aus Dänemark hinwies.
...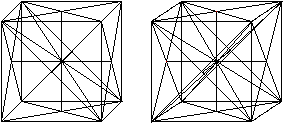 |
Für "The Shinsei Miracle" wird ein Würfel in
24 dreiseitige Pyramiden aufgeteilt. |
Das erreicht man, indem man
die vier Raumdiagonalen, die 12 Flächendiagonalen und die 4 Verbindungen
der Quadratmitten einzeichnet.
...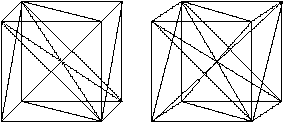 ... ... |
Es gibt eine neue Aufteilung des Würfels in 12 dreiseitige
Pyramiden, indem man die Raumdiagonalen vorgibt und nur die Flächendiagonalen
einzeichnet, die von den Endpunkten einer Raumdiagonalen ausgehen.
So entstehen 12 kongruente dreiseitige Pyramiden. |
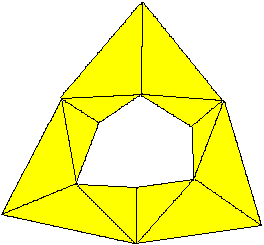 |
Baut man diese 12 Pyramiden aus Papier und verbindet
sie an den Kanten, die vorher Kanten des Würfels waren, so entsteht
ein Ring wie bei Kaleidozyklen. Man kann ihn leider nur schwer in sich
drehen, da die gegenüberliegende Kanten an den Gelenken nicht orthoganal
sind.
Doch man kann aus den 12 Pyramiden hübsche Körper
bilden. |
The Shinsei Mystery
top
Es gibt von Naoki Yoshimoto einen zweiten und bekannteren
Würfel. Er heißt "The Shinsei Mystery" oder "Yoshimoto Cube".
... |
.... ... ... |
Er besteht aus acht Würfeln oder 16 Halbwürfeln,
die miteinander durch Scharniere verbunden sind.
Man kann aus ihnen einen silbernen und goldenen Stern
bilden. |
Ich beschreibe ihn auf meiner Seite The
Shinsei Mystery.
The Shinsei
Miracle im Internet top
Französisch
Peuplier (Le Forum en Papier)
Vorlage
/ Template
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2004 Jürgen Köller
top |



 ...
...





 ...
...






 ...
...

 ...
...