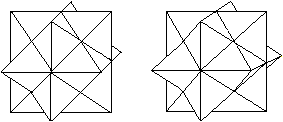|
Was ist der Oktaederstern?
...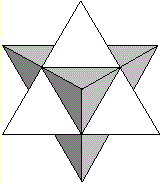 ... ... |
Zwei gleiche Tetraeder durchdringen
sich so, dass ein Stern mit acht Zacken entsteht.
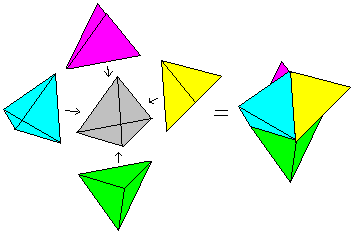
Man kann das auch so sehen: Auf die Seitenflächen
eines Oktaeders werden acht Zacken gesetzt.
Der Körper heißt Oktaederstern.
Als ein Körper, der nur von gleichseitigen Dreiecken
begrenzt wird, gehört es zu den (konkaven) Deltaedern. |
 . .
|
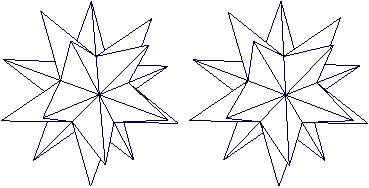
Das nebenstehende Bildpaar ermöglicht eine dreidimensionale
Sicht des Oktaedersterns. |
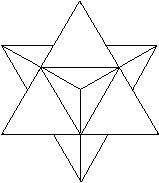
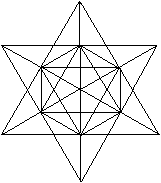
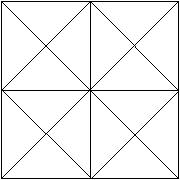
Besondere Ansichten führen
auf die Figuren Hexagramm und Quadrat.
undurchsichtig
|
durchsichtig
|
durchsichtig
|

undurchsichtig
|
Der Oktaederstern heißt auch Keplerstern.
Johannes Kepler (1571 bis 1630) untersuchte ihn wie andere vor und nach
ihm.
Er nannte ihn Stella Octangula.
Diejenigen, die in einem Oktaederstern mehr als
einen geometrischen Körper sehen, nennen ihn Merkaba.
Beziehung
zu anderen Körpern top
Beziehung zum Würfel
...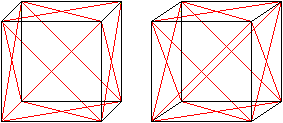 ... ... |
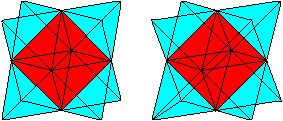
Zeichnet man alle Flächendiagonalen eines Würfels,
so entstehen zwei Tetraeder, die sich durchdringen. |
...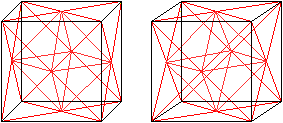 ... ... |
Verbindet man noch zusätzlich benachbarte Mittelpunkte
der Seitenflächen, also der Quadrate, so ist im Inneren das Oktaederstern
auszumachen. Man erkennt das Oktaeder und die acht Tetraeder. |
Anders ausgedrückt:
Der Würfel umhüllt den Oktaederstern. Ich nenne ihn deshalb Hüllwürfel
(Englisch: Convex hull).
Beziehung
zum Pentagondodekaeder
...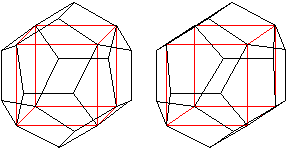 ... ... |
In einem Pentagondodekaeder
liegt ein Würfel und im Würfel ein Oktaederstern.
Da es fünf verschiedene Würfel
im Pentagondodekaeder gibt, gibt es in ihm fünf Oktaederstern.
Ich verzichte links auf die Darstellung
des Oktaedersterns. |
Einordnung
des Oktaedersterns
Setzt man Tetraeder auf ein Tetraeder, ein Oktaeder und
ein Ikosaeder, so entstehen die folgenden Sterne.
Formeln top
Ecken, Kanten und Seitenflächen
Der Oktaederstern hat e = 5+4+5 = 14 Eckpunkte, k = 8*3+12
= 36 Kanten und f = 3*8 = 24 Seitenflächen.
Betrachtet man die beiden Tetraeder, die sich durchdringen,
sind die Daten e = 8, k = 12 und f = 8.
Größen
Die Kantenlänge des Sterns sei a, dann ist die Oberfläche
O = 3*8*[(1/4)sqrt(3)a²] = 6sqrt(3)a² oder gerundet 10,39a².
Das Volumen setzt sich aus
dem Volumen der acht Tetraeder und des Oktaeders zusammen.
V=8*[(1/12)sqrt(2)a³]+(1/3)sqrt(2)a³ = sqrt(2)a³
oder gerundet 1,41a³.
Der
Radius R der Umkugel findet man als halbe Diagonale im Hüllwürfel.
D.h., R = (1/2)[sqrt(3)]*[sqrt(2)a]
= (1/2)sqrt(6)a oder gerundet 1,22a.
Vergleich
der Volumina von Tetraeder und Oktaeder
[(1/12)sqrt(2)a³]:[(1/3)sqrt(2)a³] = 1:4
(!)
Vergleich mit dem
Hüllwürfel
Der Hüllwürfel hat eine Kantenlänge von
sqrt(2)a, eine Oberfläche von 6*[sqrt(2)a]² = 12a² und ein
Volumen von [sqrt(2)a]³ = 2sqrt(2)a³.
Das Verhältnis der Oberflächen vom Stern zum
Hüllwürfel ist [6sqrt(3)a²]:[12a²] = (1/2)sqrt(3) oder
gerundet 0,8660 = 86,60%.
Das Verhältnis der Volumina vom Stern zum Hüllwürfel
ist [sqrt(2)a³]:[2sqrt(2)a³] = 1/2 = 50% (!).
Basteln des
Oktaedersterns top
Basteln mit Hilfe eines Netzes
...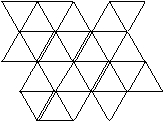 ... ... |
Auf der Webseite Stella Octangula von MathWorld
(URL unten) findet man eine Vorlage zum Basteln des Oktaedersterns. Die
Doppellinie bedeutet, dass dort ein Schnitt zu machen ist. [siehe auch
(1)]
Der Stern ist mir nicht gelungen :-(. |
...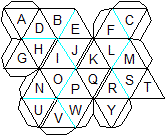 ... ... |
Im Internet fand ich eine genaue Anleitung. Die schwarzen
Linien bedeuten eine Bergfaltung, die blauen eine Talfaltung. Das Netz
ist mit Klebestreifen versehen. Die 24 Dreiecke sind nach dem Alphabet
nummeriert.
Man klebt die Tetraeder aus den Dreiecken MST, KFL, QPW,
YRV, ONI, CFE und UHG in dieser Reihenfolge. Dann schließt man den
Körper, und es entsteht das achte Tetraeder ABD. |
Das
ist das Resultat.
...
Gefalteter
Stern mit acht Zacken
... ... ... |
Der nebenstehende Stern entstand aus einem quadratischen
Blatt Papier einem russischsprachigen Video bei Youtube folgend (DYI, URL
unten).
Die Zacken sind nicht Tetraeder, sondern rechtwinklige
dreiseitige Pyramiden. |
Bascetta-Stern
mit acht Zacken
Die Zacken sind nicht Tetraeder, sondern dreiseitige
Pyramiden.
Freundlicherweise zur Verfügung gestellt von Rudolf
Kunstmann
Sonobe-Stern
mit acht Zacken
... ... ... |
Der nebenstehende Stern entstand aus 12 quadratischen
Blättern.
Die Zacken sind nicht Tetraeder, sondern rechtwinklige
dreiseitige Pyramiden.
Mehr über Sterne aus den Sonobe-Modulen findet man
auf meiner Webseite Sonobe-Stern. |
Think
3D Free
Es gibt für das IPad eine App von Paul Hangas, mit
der man auf einfache Weise aus Oktaeder und Tetraedern einen Oktaederstern
baut. -
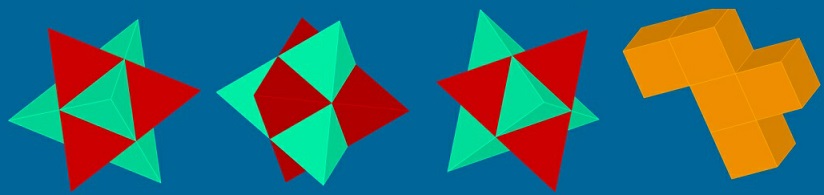
Es soll noch erwähnt werden, dass man auch Würfelkörper
zusammensetzen kann wie rechts ein Pentomino (URL unten).
...
Verschiedenes top
Hexagramm
...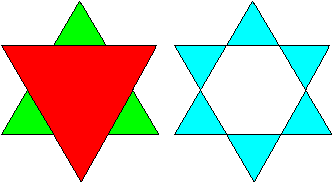 ... ... |
Im Sechseckstern kann man die zweidimensionale Version
des Oktaedersterns sehen. |
Parkettierung
des Raumes
...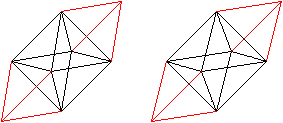 ... ... |
Setzt man auf zwei gegenüberliegende Seitenflächen
eines Oktaeders zwei Tetraeder, entsteht ein Parallelepiped. So wie die
Würfel füllen die Parallelepipede
den Raum aus. |
...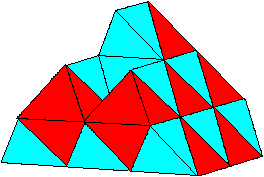 ... ... |
So sähe die Raumerfüllung in einem Ausschnitt
aus. Jedes Oktaeder ist von acht Tetraedern umgeben. Das aber ist ein Oktaederstern.
Man stellt fest:
In der Parkettierung des Raums durch Oktaeder/Tetraeder
entdeckt man Oktaedersterne. |
Zeichnung nach https://commons.m.wikimedia.org/wiki/Tessellation?uselang=de#/media/File%3AHC_P1-P3.png
Tetrakishexaeder
Verbindet man die Mittelpunkte der Dreiecke und Achtecke
eines abgestumpften Würfels, so entsteht das Tetrakishexaeder. Das
ist ein Oktaeder, auf dessen Seitenflächen dreiseitige Pyramiden liegen.
Im Unterschied zu den Tetraedern des Oktaedersterns sind die Pyramiden
flacher.
Kepler-Fraktale
Ersetzt man beim Oktaederstern die dunklen Tetraeder
wiederum durch Oktaedersterne, so erhält man ein Fraktal der Ordnung
1.
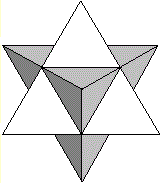
n=0
|
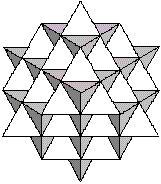
n=1
|
Das setzt man fort. Es entsteht dann eine Folge von Fraktalen.
Fraktale findet man auf den Webseiten von Paul Bourke
und des Instituts für Geometrie der Technischen Universität Dresden
(URL unten).
Oktaederstern-Zahlen
Oktaederstern-Zahlen sind figurierte Zahlen, also Zahlen,
die sich durch Figuren, in diesem Falle durch Oktaederstern, darstellen
lassen.
Sie werden nach der Formel S(n) = 2n³-n bestimmt.
Die ersten zehn Oktaederstern-Zahlen sind 1, 14,
51, 124, 245, 426, 679, 1016, 1449, 1990.
Die folgenden Überlegungen
führen zur Formel.
...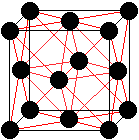 ... ... |
Ordnet man 14 Kugeln so an, dass sie in den Ecken und
in den Mittelpunkten der Seitenflächen eines Würfels liegen,
so bilden sie einen Oktaederstern. Dazu muss man sich in nebenstehender
Zeichnung vorstellen, dass die Kugeln größer sind und sich berühren.
Das ist der kleinste Oktaederstern aus Kugeln. |
... ... ... |
Das ist eine andere Überlegung.
Man bildet ein Quadrat aus vier sich berührenden
Kugeln und legt in die Mitte eine fünfte Kugel. Eine sechste Kugel
liegt unter dem Quadrat. - Die sechs Kugeln stehen für das Oktaeder.
Man legt vier Kugeln in die von drei Kugeln geformten
Mulden. Weitere vier Kugeln liegen darunter. - Die acht Kugeln stehen für
die Tetraeder und die Spitzen des Oktaedersterns. |
Es gibt immer größer
werdende Sterne, die man aus Kugeln bauen kann. Das Prinzip ist offenbar
das folgende.
Man gibt ein immer größer werdendes Oktaeder
vor und setzt auf die Seitenflächen Tetraeder.
Also geht man aus von den Oktaeder- und Tetraederzahlen.
Oktaederzahlen
...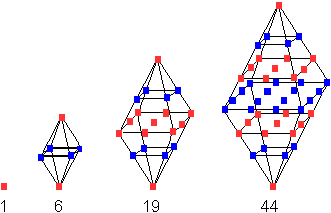 |
Die Oktaederzahlen errechnen sich nach der Formel O(n)=(1/3)(2n³+n). |
Tetraederzahlen
...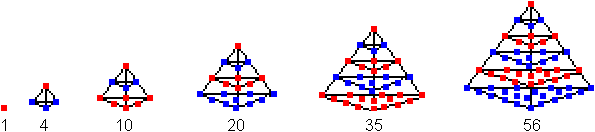 ... ... |
Die Tetraederzahlen berechnet man nach der Formel T(n)=(1/6)[n(n+1)(n+2)]. |
Es gilt für die Oktaederstern-Zahlen
S(n) = O(n)+8*T(n-1) = (1/3)(2n³+n)+8*(1/6)[(n-1)n(n+1)] = 2n³-n,
was zu zeigen war.
Auf der Wikipedia-Seite Stella
octangula number (URL unten) findet man das Bild eines Oktaedersterns
aus 124 magnetischen Kugeln.
Sternpuzzle
Verwandt mit dem Oktaederstern ist das Sternpuzzle. Der
Stern liegt auch in einem Würfel. Die Spitzen der Zacken liegen
nicht in den Ecken, sondern in den Kantenmitten des Hüllwürfels.
Die 12 Zacken sind gerade Pyramiden mit einer Raute als Grundfläche.
Oktaederstern
im Internet top
Deutsch
Christoph Pöppe (Spektrum der Wissenschaft)
Stern-
und Drachenkörper
Technische Universität Dresden (Institut für
Geometrie)
Tetraederfraktal
Wikipedia
Sterntetraeder,
Tetrakishexaeder
Englisch
Eric W. Weisstein (MathWorld)
Stella
Octangula, Tetrahedron2
Compound, Tetrakis
Hexahedron, Stella
Octangula Number
Gijs Korthals Altes
Paper
Model of a Stella Octangula
compound of two tetrahedra
George W. Hart (Virtual Polyhedra)
Compounds
of Polyhedra
N. J. A. Sloane (OEIS)
Stella octangula numbers:
a(n) = n*(2*n^2 - 1)
Paul Hangas
Think 3D Free
Wikipedia
Stellated
octahedron, Polyhedron
compound, Stella
octangula number, Tetrakis
hexahedron, Stars
(M. C. Escher), Metatron's
cube
Youtube
DIY
- Stern Oktaeder Papier
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© Dezember 2015 Jürgen
Köller
top |


 ...
... .
.


 ...
... ...
... ...
...
 ...
...
 ...
...


 ...
... ...
... ...
... ...
...


 ...
... ...
...
 ...
...