Hexagramm
Inhalt dieser Seite
Was ist ein Hexagramm?
Überschlagene regelmäßige Sechsecke
Unikursales Hexagramm
Verschiedenes
Formeln		 Satz von Pascal
Falten eines Hexagramms
Hexagramm im Internet
Referenzen
.
Diese Webseite hat den gleichen Aufbau wie meine Seiten Pentagramm, Heptagramm, Oktagramm und Nonagramm.
Eine Übersicht findet man auf der Webseite Polygramm.
Zur Hauptseite    "Mathematische Basteleien"

Was ist ein Hexagramm?
... Ein Hexagramm ist ein regelmäßiger Stern mit sechs Zacken. 

Entstehung
... Der Stern entsteht, indem man auf ein regelmäßiges Sechseck sechs gleichseitige Dreiecke stellt. 
...... Der Stern entsteht auch, indem man zwei gleichseitige Dreiecke vorgibt, ein Dreieck um 180° dreht und dann die beiden Dreiecke so übereinander schiebt, dass die Mittellinien zusammenfallen. 
...... Der Stern entsteht auch, indem man ein regelmäßiges Sechseck vorgibt und die kurzen Diagonalen einzeichnet. 
Da es nur einen regelmäßigen Stern mit sechs Zacken gibt, bezeichnet man auch das zusammengesetze Hexagramm als Hexagramm (ohne Zusatz). Man verlangt, dass Polygramme geschlossene Linien sind. 
Einordnung
...... Das Hexagramm gehört zu den zusammengesetzten Polygrammen, die durch Brüche gekennzeichnet werden.
Die erste Zahl gibt die Anzahl der Eckpunkte des erzeugenden Vielecks an, die zweite die "Sprungweite" beim Verbinden der Eckpunkte.
Unregelmäßiges Hexagramm
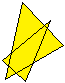...... Wenn man vom Wort her kommt, müsste man auch den nebenstehenden Stern als Hexagramm bezeichnen, denn Hexagramm  heißt "mit sechs Strichen". 

Im Sprachgebrauch ist das Hexagramm (ohne Zusatz) der regelmäßige Stern oben.
Sechszackstern
...... Ein allgemeiner sechszackiger Stern entsteht, wenn man auf ein konvexes Sechseck beliebige Dreiecke stellt. Diesen Stern sollte man nicht mehr als Hexagramm bezeichnen. Er besteht nicht aus sechs, sondern aus 18 Strichen oder Strecken. 

Er heißt Sechszackstern, Sechseckstern oder Sechsstern.

Überschlagene regelmäßige Sechsecke top
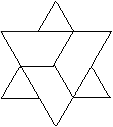
...... ... Man kann die Punkte des regelmäßigen Sechsecks auch so verbinden, dass sich die Linien überschneiden. 
Die Figuren, die dabei entstehen, bezeichnet man als überschlagene Sechsecke. 
Das "unikursale Hexagramm" hat eine große Bekanntheit erreicht. 

Es gibt durch die sechs Eckpunkte zehn weitere Figuren.
...
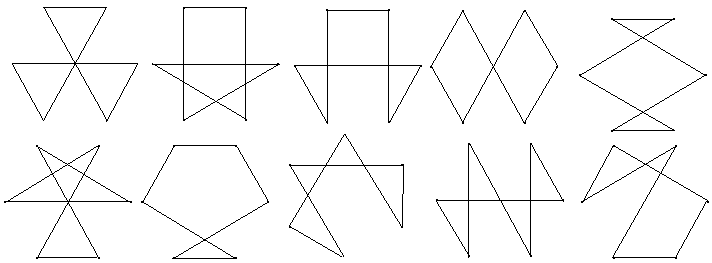
Die Figuren bilden Hamiltonkreise, da die Punkte durch eine geschlossene Linie verbunden werden.

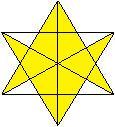
Unikursales Hexagramm    top
... Das unikursale Hexagramm wird von sechs Diagonalen gebildet. 
Es besteht aus einem Kreuz und zwei Winkel.

Unikursales Hexagramm heißt "Hexagramm aus einer Linie".

... Zeichnet man zwei Diagonalen ein, so erkennt man ein Hexagramm.

Die Winkel an der Spitze betragen 30° und 60°. 
Zwei Hauptdiagonalen und vier kurze Diagonalen des umfassenden Sechsecks bilden die Seiten.
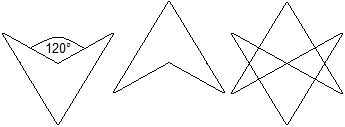...... So wie das regelmäßige Hexagramm aus zwei Dreiecken gebildet werden kann, so erzeugen zwei konkave Vierecke das unikursale Hexagramm. Man gibt zwei konkave Vierecke mit dem  kennzeichnenden Winkel von 120° vor, dreht das eine um 180° und schiebt beide so übereinander, dass ein Eckpunkt zusammenfällt.

Formeln    top
In diesem Kapitel geht es um Formeln für den 6/2-Stern. 
Auf meiner Seite Polygramm werden Formeln für den p/q-Stern hergeleitet. 

In einem Heptagramm werden bekannte Größen eines Polygramms angezeigt.
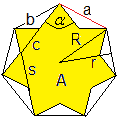... alpha - Winkel an der Spitze 
s - Seitenlänge
c - Grundseite einer Zacke
b - Schenkel einer Zacke		 R - Radius des Umkreises
r - Radius des Inkreises
A - Flächeninhalt des Sterns
a - Seitenlänge des umfassenden Fünfecks
Wenn die Seite a des umfassenden Vielecks oder Polygons gegeben ist, so gelten für den p/q-Stern die folgenden Formeln.
Winkel an der Spitze alpha 
Seitenlänge s 
Grundseite einer Zacke  c 
Schenkel einer Zacke b 
Radius des Umkreises R 
Radius des Inkreises r 
Flächeninhalt des Sterns A 		 alpha = [(p-2q)/p]*180°
s = a*sin(180°q/p)/sin(180°/p)
c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}
b = (a/2)/{cos[(q-1)/p]*180°}
R = (a/2)/sin(180°/p) 
r = (a/2)/tan(180°/p)
A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa² 
...
Für den 6/2-Stern, also für p=6 und q=2, gilt:

Winkel an der Spitze alpha = [(p-2q)/p]*180° = (2/6)*180 = 60°

Seitenlänge s = a*sin(180°q/p)/sin(180°/p) = a*sin 60°/sin 30° = sqrt(3)a

Grundseite einer Zacke c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}= a*sin 30°/cos 30° = (1/3)sqrt(3)a

Schenkel einer Zacke b = (a/2)/{cos[(q-1)/p]*180°} = (a/2)/ cos 30° = (1/2)a/(1/2)sqrt(3) = (1/3)sqrt(3)a

Radius des Umkreises  R = (a/2)/sin(180°/p) = (1/2)a/sin 30° = (1/2)a/(1/2) = a

Radius des Inkreises r =  (a/2)/tan(180°/p) = (1/2)a/tan 30° = (1/2)sqrt(3)a 

Flächeninhalt des Sterns A = (1/4){1/tan(180°/p)-tan[(q-1)/p*180°]}pa² = (3/2)(1/tan30°-tan 30°)a² = (3/2)[sqrt(3)-1/sqrt(3)]a² = sqrt(3)a²



Das Hexagramm hat den Flächeninhalt A1 = sqrt(3)a².

Die vier weißen, halben gleichseitigen Dreiecke haben zusammen einen Flächeninhalt von 
A2 = 2*(1/4)sqrt(3)c² = (1/2)sqrt(3)[(1/3)sqrt(3)]² = (1/6)sqrt(3)a².

Damit ist der Flächeninhalt des unikursalen Hexagramms 
A = A1 - A2 =  sqrt(3)a²-(1/6)sqrt(3)a² = (5/6)sqrt(3)a².

Flächenvergleiche
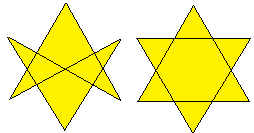...... Die beiden Flächeninhalte stehen im Verhältnis 20 : 24 = 5 : 6
Die drei Flächeninhalte stehen im Verhältnis 1 : 3 : 9.

Verschiedenes     stop
Rauten
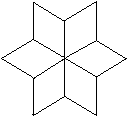
... Man könnte die Liste der drei Beschreibungen von oben noch erweitern: 
Gibt man sechs 60-Grad-Rauten vor, so kann man aus ihnen ein Hexagramm legen.

...... Früher waren Salmiakpastillen in Rautenform in Mode. Man feuchtete den (sauberen?) Handrücken an und legte aus sechs Pastillen einen Stern. Dann leckte man die Pastillen weg. 
Keltischer Knoten
...... Zeichnet man die Linien des Hexagramms dicker und dann abwechselnd Brücken und Unterführungen, so entsteht ein geflochtener Stern. 
74 Knoten
...... ..... Laut Wikipedia kennzeichnet man die Knoten in der Knotentheorie durch zwei Zahlen. 
Die erste Zahl gibt die Anzahl der Kreuzungen an, die zweite Zahl nummeriert die Knoten durch. 
So ist 71 der Knoten, der aus einem Heptagramm hervorgeht. Er ist der einfachste.
Linien im Hexagramm
...
Kein Hexagramm
Parallelprojektionen regelmäßiger Körper
1 Oktaeder, 2 Kuboktaeder, 3 Abgestumpfter Würfel, 4 Abgestumpftes Dodekaeder, 
5 Kleines Rhombenkuboktaeder, 6 Kleines Rhombenikosidodekaeder, 7 Ikosaeder
...
Dreiecke
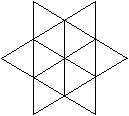... Zwölf gleichseitige Dreiecke bilden ein Hexagramm.
Damit gehört diese Figur zu den Polyiamonds. 
... ......................................................
Mehr finden man auf meiner Seite Polyiamonds.
Fraktal
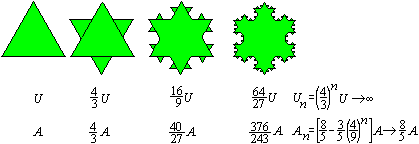...... Ein Fraktal ist eine Folge von Figuren, bei der sich die Ausgangsfigur in den folgenden Figuren als ähnliche wiederfindet.

Mehr auf meiner Seite Geometrische Folgen und Reihen
Fertige Hexagramme
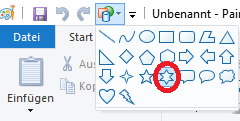
Zu Windows 10 gehört das Zeichenprogramm MSPaint. Es bietet die Möglichkeit, fertige Hexagramme aufzurufen (und zu verfälschen).
......
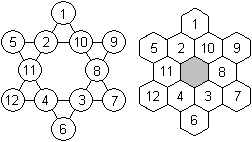
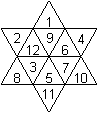
Sternzahlen
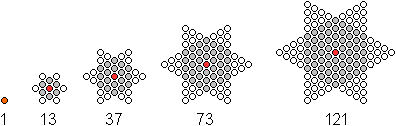...... Bei dieser Folge von Hexagrammen werden die Kreise gezählt. 

Mehr auf meiner Seite Figurierte Zahlen
Halma hat 121 Felder.
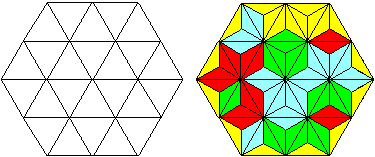
Parkettierungen

Von meiner Seite Parkettierungen
Von meiner Seite Triominos
Basteln eines Sterns aus Perlen
...... Man benötigt für diesen Stern 30 Holzperlen und einen etwa 100 cm langen Draht mit einem Durchmesser von etwa 0,3 mm. (Ich habe beides bei Kik gekauft.)

Der Draht wird zu drei geschlossenen Ringen gebogen und nimmt dabei Perlen auf.. 

Für den ersten Umlauf zieht man 12 Perlen auf den Draht auf und verdrillt die beiden Enden, wobei man das eine Ende kurz wählt. Es entsteht ein Ring.
Beim zweiten Umlauf kommt 6x ein Perlenpaar dazu. 
Beim dritten Umlauf werden sechs Einzelperlen hinzugefügt, die die Spitze einer Zacke bilden. 

Zum Schluss werden die Drahtenden verdrillt und abgeschnitten. 
Bild dazu...

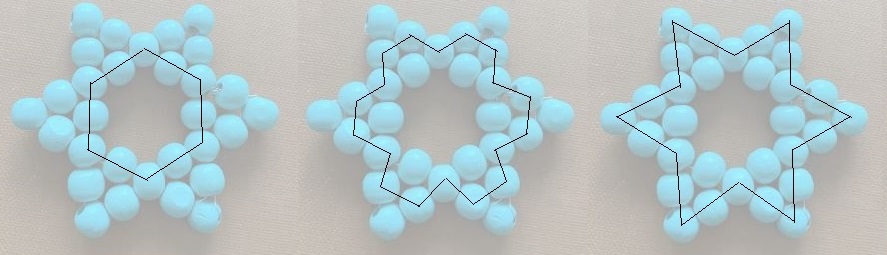
"Mrs. Greenhouse" beschreibt das Basteln dieses Sterns anhand einer Fotoreihe, URL unten.
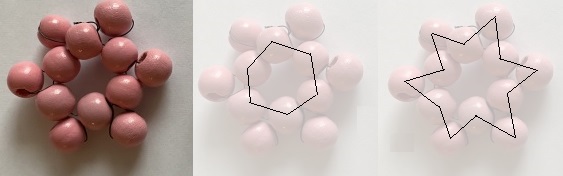
Schnell gemacht
...
Oktaederstern
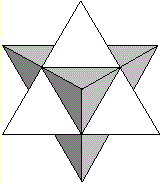... Der Oktaederstern ist sozusagen das dreidimensionale Hexagramm. 

Mehr über ihn auf meiner Seite Oktaederstern.
Magische Sterne
... Mehr auf meiner Seite Magische Quadrate..........................
Hexagramm und Doppelpyramiden aus Stabmagneten

Mehr Figuren und Körper findet man auf meiner Webseite Körper aus 24 Stabmagneten.

Satz von Pascal top
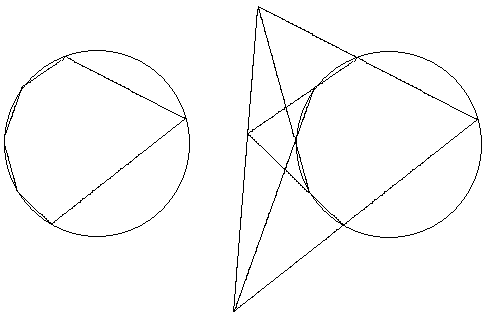...... Wie heißt der Satz von Pascal?

Man gibt sechs Punkte auf einer Kreislinie vor und bildet ein Sechseck.
Verlängert die Seiten des Sechsecks, so entstehen drei Schnittpunkte. 

Der Satz besagt, sie liegen auf einer Geraden.

Dieses ist ein Spezialfall des Satzes. 

 

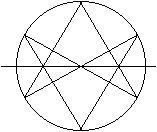...... Das unikursale Hexagramm ist kein konvexes Sechseck, sondern ein "überschlagenes".

Die drei Geradenpunkte liegen im Inneren des Kreises. 
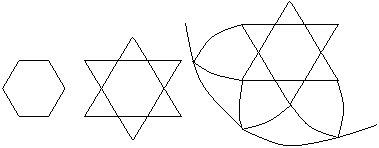...... Und auch für das regelmäßige Hexagramm gilt der pascalsche Satz. 

Man muss allerdings akzeptieren, dass die drei Schnittpunkte "im Unendlichen" liegen.
Das ist möglich, nur verlässt man dann die euklidische Geometrie, sprich Schulgeometrie, und gelangt zur projektiven Geometrie. Da wird kein Unterschied gemacht zwischen endlichen und unendlichen Punkten.
Es ist noch eine Erweiterung des pascalschen Satzes möglich: An Stelle der Kreislinie kann man Kegelschnitte wählen.

Falten eines Hexagramms   top
(Author: Shizo Fujimoto)
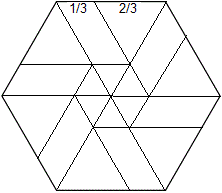... Wer das Hexagramm falten will, sollte die nebenstehende Figur auf ein halbes A4-Blatt ausdrucken und das Sechseck dann ausschneiden. 

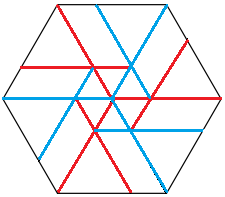... Dann muss man so falten, dass die roten Linien zu Talfaltungen und die blauen zu Bergfaltungen werden. 

Wichtig ist, dass die Faltlinien nachgezogen, also geschärft werden. 
... Wenn man sich konsequent an die Täler und Berge hält, kann man das Sechseck zu diesem kleinen Sechseckstern falten.
... Das ist mein Ergebnis. 
...... Volker Sayn faltete diesen Papierstern.

Er wurde aus einem Blatt mit Rot vorne und Weiß hinten gefaltet.

So sieht man, dass Vorder- und Rückseite dieselbe Struktur haben. 
...... ... Ich muss zugeben, dass der fertige Stern eine große Hilfe bei dieser kniffligen Faltarbeit war.

Deshalb zeige ich Vorder- und Rückseite halb geöffnet.
Der Papierstern beeindruckt, da sich der geöffnete Stern fast von selbst wieder schließt.
Kunstvoll gefaltete Sterne   (Der Falter ist Volker Sayn.)
...

Hexagramm im Internet top

Deutsch

Mrs. Greenhouse (Do It Yourself & Lifestyle)
Sterne aus Holzperlen

Online-Rechner
Hexagramm, Unikursales Hexagramm

Wikipedia
Hexagramm, Unikursales Hexagramm,  Satz vonPascal,  Stern (Geometrie)

Englisch

Eric W. Weisstein (World of Mathematics)
Hexagram, Magic Hexagram, Pascals Theorem, Star Polygon, 

Wikipedia
Hexagram. Unicursal hexagram, Pascal s theorem, Star polygon

Youtube
Entstehung dreier Kolams
rangoli designs for Diwali 2023, hexagon kolam design, 5X3 dots Rangoli Design

Referenzen   top
(1) https://de.wikipedia.org/wiki/Hexagramm
(2) http://mathgardenblog.blogspot.com/2013/06/hexagrammum-mysticum1.html
(3) Martin Gardner: Mathematischer Zirkus, Berlin 1988 (ISBN 3550076924)


Feedback: Emailadresse auf meiner Hauptseite 

URL meiner Homepage:
https://www.mathematische-basteleien.de/

© 11/2023 Jürgen Köller

top
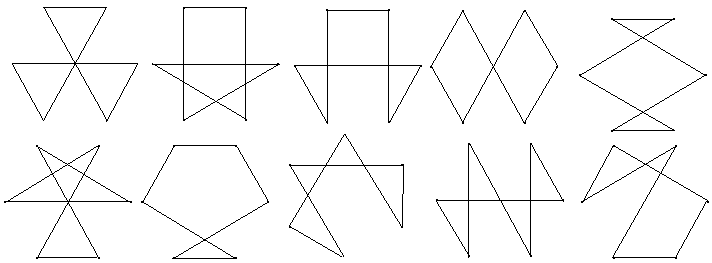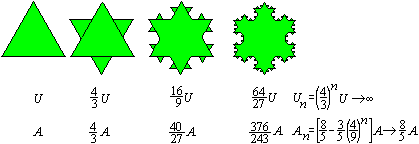
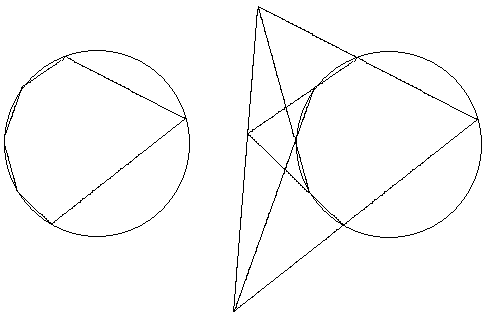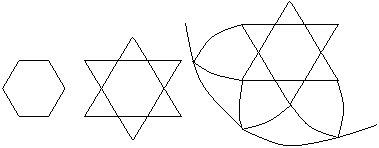