|
Was ist der Kusudama-Stern?
... ...
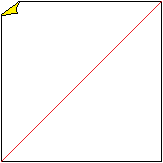
Das ist die erste von 20 Zacken ...
Das ist die erste von 20 Zacken
|
Im Internet fand ich unter dem Namen Kusudama-Stern eine
Reihe von Sternen, die wie der Bascetta- und der Sonobe-Stern aus 30 Modulen
zusammengesteckt und die auch bekrönte Ikosaeder sind.
Ich habe für diese Seite den
"Origami Igel Kusudama" ausgewählt, dessen Bau in einem Youtube-Video
(gehört zu "Katrin Origami-Seite") beschrieben wird. Die Erfinderin
des Moduls und des Sterns ist Ekaterina Lukasheva. |
Meine
Wahl fiel auf den Stern, weil die Zacken spitzer und dadurch ansehnlicher
sind als die Zacken des Bascetta-Sterns. - Es ist bemerkenswert, dass das
Modul die Erzeugung eines Winkels von 30° allein durch Falten benutzt
(Schritt 4 unten).
Zum
Sonobe-Stern und zum Bascetta-Stern gibt es eigene Seiten.
Falten
des Kusudama-Moduls top
Material
... ... ... |
Man benötigt für den Stern 30 Quadrate aus
Papier.
Da böten sich die Notizzettel 9cm x 9cm an, die man
z.B. in Schreibwarengeschäften kaufen kann.
Sie waren gut geeignet für den Bascetta- und den
Sonobe-Stern. Aber für diesen Stern sind sie meiner Meinung nach ungeeignet.
Man muss wohl wie im erwähnten Video dünnes Origami-Papier verwenden.
Das habe ich auch getan und es ging besser. |
12
Schritte
1
2
...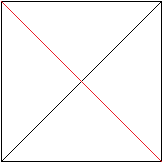 ......... ......... |
Falte an der roten Linie und entfalte wieder.

 |
3
...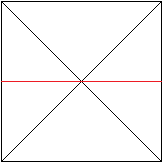 ... ... |
Falte an der roten Linie und entfalte wieder.
 |
4
...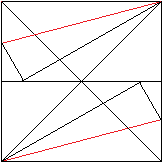 ... ... |
Falte an den roten Linien so, dass die Ecken des Quadrates
die Mittellinie berühren.
 |
5
...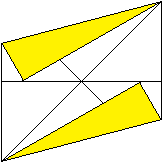 ... ... |
Das müsste dann so aussehen
wie in der rechten Figur.

 |
6
..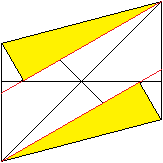 .... .... |
Falte an den roten Linien. Die untere Linie und die obere
müssten auf die Diagonale treffen.
 |
7
...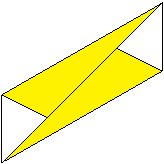 |
Das müsste dann so aussehen.

 |
8
...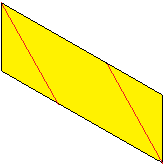 |
Drehe das Modul um und falte an den roten Linien. Entfalte
wieder.

 |
9
...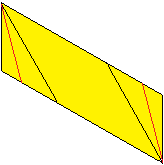 |
Falte an den roten Linien.

 |
10
...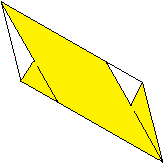 . . |
Das müsste dann so aussehen. Entfalte.


 |
11
...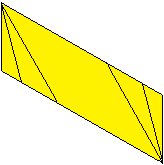 |
Das müsste dann so aussehen.

 |
12
Zusammenbau des
Sterns top
...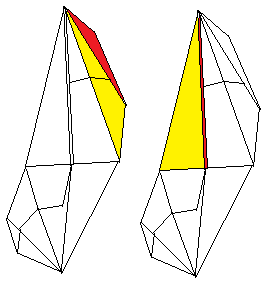 |
Verbinde zwei Module.
Stecke dazu die rote Lasche in die rote Tasche. Dann
liegen die gelben Dreiecke aufeinander.


 |
... ... ... |
Das müsste dann so aussehen.
Die Lasche blieb in der Tasche nicht stecken; eine Büroklammer
hilft.

 |
... ....... ....... |
Umfasse die beiden verbundenen Module mit einem dritten
Modul. Die erste Zacke ist fertig.
Dann fügt man Schritt für Schritt weitere Module
hinzu und formt weitere Zacken. Dabei achtet man darauf, dass immer fünf
Zacken einen Kranz bilden.


|
... ... ... |
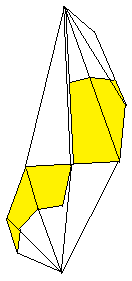
An dieser Stelle müsste eigentlich der fertige Kusudama-Stern
mit 20 Zacken stehen.
Aus verschiedenenen Gründen habe ich mich mit einem
"Trost-Stern", einem Stern aus 12 Modulen mit acht Zacken, begnügt.
Der Stern ist ein bekröntes Oktaeder, bei dem die
Kränze immer aus vier Zacken bestehen. |
Meine
Erfahrung mit Notizzetteln top
... ... ... |
... ... ... |
Faltet man die Module aus Notizzetteln, so ist das Ergebnis
unbefriedigend.
- Wie man links sieht, ist die Spitze einer Zacke verfranzt.
Es ist kaum möglich, fünf Faltlinien exakt an einer Ecke des
Notizzettels zusammenlaufen zu lassen. Das Papier reißt auch oft
ein.
- Dann sind die Taschen so offen und die Laschen so klein,
dass ich Büroklammern benötigte, um die Module zusammen zu halten. |
Etwas Mathematik top
...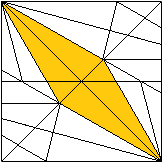 ... ... |
Entfaltet man das Modul, so erkennt man die Seitenflächen
zweier Zacken als gleichschenklige Dreiecke.
Der Winkel an der Spitze eines Dreiecks beträgt wegen
des Faltvorgangs 30°.
Die Höhe eines Dreiecks ist die halbe Diagonale des
Quadrats mit der Seitenlänge a. |
Auf
drei Fragen soll eingegangen werden.
1. Frage
Die Quadratfläche Aq
des Moduls wird nur zu einem kleinen Teil genutzt. Wie viel Prozent sind
das?
Antwort
...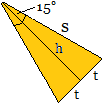 ... ... |
Im halben gleichschenkligen Dreieck sind die Höhe
h=(1 /2)sqrt(2)*a und der Winkel von 15° bekannt.
Dann gilt tan(15°) = t/h. Dann ist t = h/tan(15°).
Mit tan(15°) = 2-sqrt(3) ist t= [sqrt(2)-(1/2)sqrt(6)]a
= 2*[2sqrt(2)-sqrt(6)]a .
Der Flächeninhalt der Seitenfläche einer Zacke
ist A = (1/2)(2t)h = th = (1/2)[2-sqrt(3)]a². |
Zwei gleichschenklige Dreiecke tragen
zur Bildung des Stern bei. Sie haben den Flächeninhalt 2A.
Das Quadrat des Moduls hat die
Fläche Aq = a². Dann gilt gerundet 2A/Aq =26,8%.
Ergebnis
Etwa 27% der Fläche des Ausgangsquadrats
werden genutzt.
2.
Frage
Wie groß ist die Höhe
H einer Zacke?
Antwort
... ... ... |
Vorweg
Es gilt s = h/cos(15°) =[2sqrt(2)/(sqrt(2)+sqrt(6))]a
= [sqrt(3)-1]a.
Dabei ist cos(15) = (1/4)[sqrt(2)+sqrt(6)].
Die Höhe im gleichseitigen Dreieck mit der Seite
2t ist h' = (1/2)sqrt(3)(2t). |
...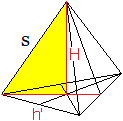 ... ... |
Nach dem Satz des Pythagoras gilt
H² = s²-[(2/3)h']² = [sqrt(3)-1]²a²-[(2/3)(1/2)sqrt(3)2t]a²
= [sqrt(3)-1]²a²-[(2/3)sqrt(3)t]a²
=[sqrt(3)-1]²a²-[(2/3)sqrt(3)(sqrt(2)-(1/2)sqrt(6))]²a²
= [sqrt(3)-1]²a²-[2/3sqrt(6)-sqrt(2)]²a²
= [4-2sqrt(3)]²a²-[14/3-8/3sqrt(3)]a²
= [-2/3+2/3sqrt(3)]a².
Dann ist H = (1/3)sqrt[6sqrt(3)-6]a. |
Ergebnis
Die Höhe einer Zacke beträgt H = (1/3)sqrt[6sqrt(3)-6]a
oder gerundet H = 0,699a.
Ist die Seitenlänge des Ausgangsquadrates a = 9
cm, so ist die Höhe H = 6,3 cm groß.
3.
Frage
Wie groß ist der Stern?
Damit ist die Entfernung e der Spitzen zweier gegenüber
liegender Zacken gemeint.
Antwort
Der Abstand gegenüberliegender Seitenflächen
des Ikosaeders ist der doppelte Radius des Inkreises.
d = (1/6)[3sqrt(3)+sqrt(15)](2t) = (1/6)[3sqrt(3)+sqrt(15)][2sqrt(2)-sqrt(6)]a
oder gerundet d=0,571a.
Die Entfernung ist gerundet e = 2H+d = 2*0,699a+0,573a
= 1,971a.
Ergebnis
Ist die Seitenlänge des Ausgangsquadrates a = 9,0
cm, so wird der Stern 17,7 cm groß.
Vergleich
von drei Sternen
|
a=9,0cm
|
Sonobe-Stern
|
Bascetta-Stern
|
Kusudama-Stern
|
|
2A/Aq
|
12,7%
|
20,0%
|
26,8%
|
|
H
|
0,29a = 2,6cm
|
0,49a = 4,4cm
|
0,70a = 6,3cm
|
|
e
|
1,04a = 9,4 cm
|
1,45a = 13,1cm
|
1,97a = 17,7cm
|
|
Sonobe-Stern
|
Bascetta-Stern
|
Kusudama-Stern
|
|
|

|
Kusudama-Sterne
im Internet top
Zehn Links zu Sternen mit 20 Zacken
1.Stern: Sonobe-Stern
2.Stern: Bascetta-Stern
3. Stern: Origami
Igel Kusudama (Youtube)
Und weiter
4. Stern: Origami
Radianta Kusudama (Youtube)
5. Stern: Origami
Modular Star (Bascetta-Stern, gespiegelt)
6. Stern: How
to fold an Origami Modular Star (Youtube)
7. Stern: 30-unit
Sky Star Kusudama (Creator: Maria Sinayskaya) (Youtube)
8. Stern: Origami
Kusudama/ 3D Star Ball for Christmas/ Paper 30-point Star (Youtube)
9. Stern: Origami
Estramallar Origami (Youtube)
10. Stern: Tutorial
for Origami Sonobe Variation Kusudama 30 (Youtube)
Weitere Links
Elisa (japanliebe.de)
kusudama
– was haben origami-Bälle mit Medizin zu tun?
Katrin
Origami
die Kunst des Papierfaltens
Wikipedia
Kusudama
Youtube
PopUp
Star
Youtube
Kusudama
estrella Ostrum
Youtube
Dreiecke
durchdringen sich
Feedback: Email address on my main page
This
page is also available in Englisch.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2022 Jürgen Köller
top |
 ...
...
 .
.

 ...
... ....
.... .........
......... ...
... ...
... ...
... ....
....


 .
.

 ...
... ...
... ...
... ...
... ...
... ...
... ...
...
