|
Was ist eine Kugel?
...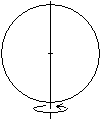 ... ... |
Eine Gerade verläuft durch den Mittelpunkt eines
Kreises.
Rotiert der Kreis um diese Gerade, so entsteht eine Kugel.
Alle Punkte der Kugeloberfläche haben vom Mittelpunkt
die gleiche Entfernung. |
Gleichungen
der Kugel top
...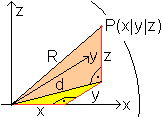 ... ... |
Es sei Punkt P ein beliebiger Flächenpunkt der Kugel
mit dem Radius R in einem räumlichen, kartesischen Koordinatensystem.
Zeichnet man seine Koordinaten als Strecken ein (rot), so entstehen zwei
rechtwinklige Dreiecke, für die der Satz des Pythagoras gilt: Das
führt zu R²=z²+d²=z²+(x²+y²)=x²+y²+z².
Ergebnis: Die Koordinatengleichung einer Kugel ist x²+y²+z²=R². |
Hat die Kugel den Mittelpunkt
M(x0|y0|z0), so heißt die Koordinatengleichung
(x-x0)²+(y-y0)²+(z-z0)²=R².
Man kann die Koordinaten
auch durch einen Term mit zwei Parametern wie folgt beschreiben.
x=Rsin(u)cos(t)
y=Rsin(u)sin(t)
z=Rcos(u)
Es ist der gleiche Kreis, wie die folgende Rechnung zeigt.
x²+y²+z²=R²[sin²(u)cos²(t)+sin²(u)sin²(t)+cos²(u)]=R²{sin²(u)[cos²(t)+sin²(t)]+cos²(u)}=R²[sin²(u)+cos²(u)]=R²
Darstellungen
einer Kugel top
1 Der Umriss einer Kugel ist ein Kreis, und damit ist der
Kreis das Bild einer Kugel.
2 Ein besseres Bild entsteht, wenn man noch zusätzlich
zum Kreis den Dreh-Kreis in der Position senkrecht zur Zeichenebene als
Schrägbild einzeichnet.
3 Man könnte auch einen Punkt des Drehkreises in
der "Äquatorebene" verfolgen.
4 Man findet in Büchern eine einfache Zeichnung,
in der die Kugelkrümmung durch wenige Linien angedeutet wird.
5 Die Krümmung wird deutlicher durch die Methode
des Raytracings.
...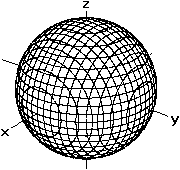 ... ... |
Ein aufwändiges Bild entsteht, wenn man durch die
Kugel in gleichen Abständen parallel zu den Hauptebenen eines räumlichen
Koordinatensystems Ebenen legt und die Schnittlinien festhält.
Alle Schnittlinien sind Kreise. Gehen die Kreise durch
den Mittelpunkt der Kugel, entstehen "Großkreise". Sie haben mit
der Kugeln den Radius r gemeinsam. Die übrigen Schnittlinien sind
"Kleinkreise". Sie haben einen Radius kleiner als r.
Das Bild entstand mit dem Freeware-Programm Winplot (URL
unten) mit Hilfe der Gleichung x²+y²+z²=4. |
...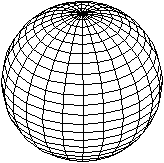 ...... ...... |
Das Programm Winplot ermöglicht es auch, die Kugel
aus Breiten- und Längenkreisen zu bilden.
Dazu wählt man die Parameterdarstellung
x=sin(u)cos(t)
y=sin(u)sin(t)
z=cos(u)
mit R=1 und 0<=t<=2*pi und 0<=u<=pi. |
Auf meiner Seite Torus
erkläre ich, wie man mit dem Programm Winplot Körper dieser
Art zeichnet.
Größen der
Kugel top
... ... ... |
Eine Kugel wird üblicherweise durch den Radius r
gegeben.
Daraus lassen sich das Volumen V und die Oberfläche
O berechnen.
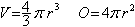
|
Erste
Herleitung der beiden Formeln
...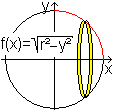 ... ... |
Man stelle sich vor, der rote Viertelkreis rotiere um
die x-Achse. Dann entsteht eine Halbkugel.
Für Rotationskörper dieser Art gibt es Formeln
für das Volumen und für die Oberfläche.
Zur ihren Herleitungen zerlegt man sie in Scheiben und
summiert diese Volumina, für die Oberfläche summiert man die
Mäntel von Kegelstümpfen. Das führt zu Integralen. |
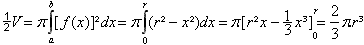
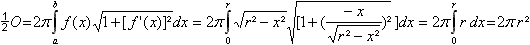
Zweite
Herleitung der beiden Formeln
Man kann auch Integrale umgehen.
Volumen
Nach dem Satz des Cavalieri haben zwei Körper das
gleiche Volumen, wenn Schnittflächen in derselben Höhe den gleichen
Flächeninhalt haben.
...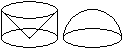 ... ... |
Zwei Körper dieser Art sind eine Halbkugel und ein
Restkörper. Dieser entsteht, wenn man einen Kegel aus einem
Zylinder herausnimmt. |
Restkörper
...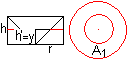 ... ... |
Beim Zylinder sind Radius und Höhe gleich.
Der Kegel mit den gleichen Abmessungen wird kopfüber
hineingesteckt.
Es entsteht ein Restkörper mit dem Volumen V=pi*r²h-(1/3)pi*r²h=(2/3)pi*r²h. |
Legt man durch den Restkörper in beliebiger Höhe
h' (0<h'<h) eine Schnittebene, so ist die Schnittfläche ein
Kreisring mit dem Flächeninhalt A1=pi*(r²-y²)=pi*(r²-h'²).
Halbkugel
...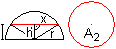 ... ... |
Legt man durch eine Halbkugel mit dem gleichen Grundkreis
wie der Zylinder einen Schnitt in gleicher Höhe wie oben, so entsteht
ein Kreis mit dem Flächeninhalt. A2=pi*x²=pi*(r²-h'²). |
Es gilt also A1=A2 und weiter Vhalbkugel=(2/3)pi*r²h
und Vkugel=(4/3)pi*r²h.
Oberfläche
Die Kugeloberfläche als Fläche
zweiter Ordnung kann man nicht in der Ebene ausbreiten. Dadurch wird eine
elementare Bestimmung schwierig. Es gibt eine Plausibilitätserklärung.
...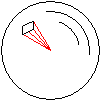 ... ... |
Man greife ein beliebig kleines Flächenelement "delta
A" heraus und verbinde die Begrenzungslinie mit dem Mittelpunkt der Kugel.
Dann entsteht ein beliebig kleiner Kegel mit dem Volumen
(delta V)=(1/3)(delta A)r.
Addiert man diese gedachten Kegel, so ergibt sich [Summe
der (deltaV)]=(1/3)[Summe der (delta A)]r oder V=(1/3)Or.
Mit V=(4/3)pi*r³ ergibt sich O=4pi*r². |
Kugelteile top
Kugelabschnitt oder Kugelsegment
Gelb: Kugelkappe, -haube, -kalotte

V=(1/3)*pi*h²(3r-h)=
pi*h[(1/2)a²+(1/6)h²]
M=2pi*rh
O=pi*(a²+2rh) |
Kugelausschnitt oder Kugelsektor
.
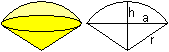
V=(2/3)*pi*r²h
O=pi*r(2h+a) |
Kugelschicht, Gelb: Kugelzone
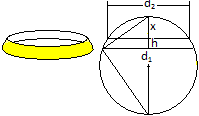
V= (1/24)pi*h(3d1²++3d2²+4h²)
M=2pi*rh |
Kugelkeil
gelb: Kugelzweieck (M)
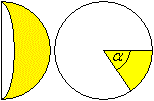
V=(4/3)pi*r³(alpha/360°)
M=4pi*r²(alpha/360°) |
Kugelring
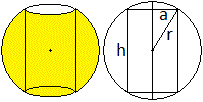
V= (1/6)pi*h³
O = 2pi*h(r+a) |
Hohlkugel
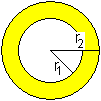
V = (4/3)pi*(r2³-r1³)
O = 4pi*(r1²+r2²) |
Mehr auf meiner Webseite Kugelteile
Flächen
zweiter Ordnung top
Die Kugel gehört zu den Flächen zweiter Ordnung.
Sie ergeben sich, wenn man in einem räumlichen kartesischen
Koordinatensystem die Gleichung Ax+By+Cz+Dxy+Eyz+Fzx+Gx+Hy+Kz+L=0 graphisch
darstellt.
Bei bestimmten Werten für die Variablen A bis L
ergeben sich im Wesentlichen die folgenden Flächen.
Pyramiden aus Kugeln
top
...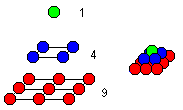 ... ... |
Man kann Kugeln zu einer Pyramide aufschichten. Die Anzahl
der Kugeln in einer Schicht ist eine Quadratzahl: 1,4,9,16,... , allgemein
n². Bildet man die Summe der Kugeln schichtweise, so erhält man
die "Pyramidenzahlen" 1,5,14,30,... , allgemein 1+4+9+16+...+n²=n(n+1)(2n+1)/6. |
Früher bewahrte man so Kanonenkugeln auf und konnte
mit Hilfe der Anzahl der Schichten auf die Anzahl der Kanonenkugeln schließen.
...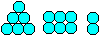 ... ... |
Klebt man 14 Kugeln zu zwei Sechsergruppen und einem
Paar zusammen, so erhält man ein Puzzle:
Man muss die drei Stücke zu einer Pyramide zusammensetzen. |
... ... ...
|
Es geht auch komplizierter. ........................... |
Es sieht auch schön aus, Kugeln zu Pyramiden zu stapeln.
Dann müssen die Kugeln der untersten Schicht in
Mulden oder in einem Rahmen liegen.
Erde als Kugel top
Die Planeten und die Sonne sind kugelförmig. Sie
werden von der Eigengravitation zusammengehalten.
Als die Teilchen noch gegeneinander verschiebbar waren,
bildete sich ein stabiler Zustand:
... ... ... |
Die Oberfläche stellte sich so ein, dass die Anziehungskräfte
senkrecht zu ihr und dann auf einen Mittelpunkt gerichtet waren. Aus diesen
Urzeiten stammt die Kugelform.
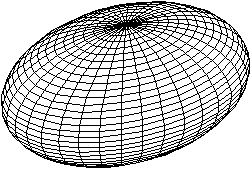
Bei der Erde kommt noch hinzu, dass sie durch die Eigendrehung
an den Polen abgeflacht und am Äquator geweitet ist. Der Unterschied
der Entfernungen vom Mittelpunkt ist aber nur 0,34%. |
Sonne/Mond/Erde
Auf vielen Schulhöfen wird gerne unser Sonnensystem
oder einfach nur das System Erde/Mond aufgezeichnet.
Hier sind Daten. [d( ) sind Durchmesser, e( / ) Entfernungen
der Himmelskörper]
Für einen Maßstab 1cm=1000 km oder 1 :
100.000.000 gilt:
d(Erde)=12,7cm, d(Mond)=3,5cm,
e(Erde/Mond)=3,84m
Zum Vergleich die Daten der Sonne: d(Sonne)=13,2m,
e(Erde/Sonne)=1,50 km (!)
Wem das Modell zu klein ist, der kann die fünffachen
Längen wählen.
Landkartenproblem
... ... ...
|
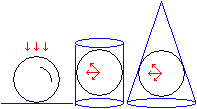
Die Kugel gehört zu den doppelt gekrümmten
Körpern und kann nicht in der Ebene ausgebreitet werden. Will man
die Oberfläche - wie für Landkarten nötig - eben darstellen,
muss man sich mit Projektionen behelfen. Man projiziert die Kugel auf eine
Tangentialebene oder legt um die Kugel einen Zylinder oder einen
Kegel und projiziert auf die Mäntel. Die Mäntel lassen sich eben
ausbreiten. In allen Fällen gibt es Verzerrungen der Kugeloberfläche.
Sie sind in der Umgebung des Berührpunktes bzw. der Berührlinien
am geringsten. |
Dieses ist ein Einstieg in das Gebiet der Kartographie. Mehr
bei Wikipedia "Kartenprojektion" (URL unten).
Sind
Atome Kugeln? top
Sind Atome Kugeln? Eher nicht.
Doch die Frage: "Kann man sich Atome als Kugeln vorstellen?" muss man bejahen.
Man nähert sich in den Naturwissenschaften der Wirklichkeit
oft in Form von Modellen.
Gerade für Atome sind verschiedene Modelle bekannt.
Einige sind nur noch historisch zu sehen.
Es werden in Folgendem drei Modelle angesprochen: Das
Teilchenmodell, das Bohrsche Atommodell und das Orbitalmodell.
Teilchenmodell
Man stelle sich ein "ideales Gas"
vor.
...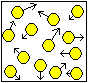 ... ... |
Es besteht aus Teilchen (dargestellt
als Kugeln), die sich in einem abgeschlossenen Behälter frei bewegen.
Sie haben eine Masse, aber kein Eigenvolumen. Sie stoßen elastisch
aufeinander und auf die Wand.
Mit diesem einfachen Bild kann
man u.a.das Boyle-Mariottesche Gesetz pV=c herleiten und die Konstante
c als kinetische Energie der Teilchen deuten (1, Seite 87f.). |
Die Konstante c wiederum ist nach der
allgemeinen Gasgleichung pV=CT proportional zur absoluten Temperatur. So
folgt, dass die Temperatur durch die kinetische Energie der Teilchen bestimmt
wird. Das ist eine Vorstellung, die sich immer wieder als richtig herausgestellt
hat.
Streng genommen gibt es kein ideales Gas. Leichte Gase
wie Wasserstoffgas kommen diesem Bild noch am nächsten.
>Die Teilchen sind Moleküle und kompliziert aufgebaut
und auch nicht einheitlich.
>Zwischen den Teilchen gibt es Anziehungskräfte
(Van Der Waalschen Kräfte)
>Die Teilchen haben ein Eigenvolumen.
Für reale Gase haben die Gesetze des idealen Gases
somit Grenzen und sind nur - wenn auch gute - Näherungsgesetze.
Es gibt darüber hinaus Erscheinungen, die mit diesem Bild nicht erfasst
werden.
Bohrsches
Atommodell des Wasserstoffs
... ... ...
|
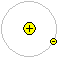
In diesem Modell hat man sich das Wasserstoff-Atom nach
außen hin als eine Kugel vorzustellen.
Die Kugel hat eine Struktur. Ein Elektron bewegt sich
ähnlich der Bewegung der Erde um die Sonne um einen Atomkern,
einem Proton. Die anziehende Kraft entsteht nicht durch die Gravitation,
sondern durch die elektrische Kraft zwischen zwei unterschiedlichen Ladungen. |
...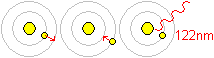 ... ... |
Die Bahn eines Elektrons ist nicht fest, sondern es kann
auf bestimmte Kreisbahnen angehoben werden, wenn eine passende Energie
zugeführt wird. Dieser angeregte Zustand ist nicht stabil, das Elektron
fällt zurück und sendet dabei eine Lichtwelle aus. |
Diese Vorstellung ist anschaulich. Die Frequenzen des ausgesandten
Lichtes lassen sich näherungsweise bestimmen. Das Auftreten von Spektralserien
sowie der Ionisierungsenergie werden verstehbar.
... ... ... |
Es gibt Phänomene des Wasserstoffs, die sich so
nicht erklären lassen. Ein Verallgemeinerung auf größere
Atome ist nicht möglich. Nach Aussage der Quantenphysiker ist das
Planetenbild schief. Es ist somit schon oft aus den Schulbüchern verschwunden.
Das Bohrsche Atommodell ist also eher historisch zu sehen.
Es lebt in abgewandelter Form als Schalenmodell zum Ordnen
der chemischen Elemente weiter. |
Orbitalmodell
Heute macht man sich von einem Wasserstoffsatom eine
Vorstellung, die vom Wellencharakter des Elektrons bestimmt wird.
...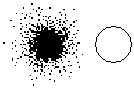 ... ... |
Es gibt einen Atomkern. Das Elektron hält sich in
der Umgebung des Kerns auf mit einer bestimmten Aufenthaltswahrscheinlichkeit.
Man erhält eine exakte Kugel, wenn man z.B. 50% Aufenthaltswahrscheinlichkeit
"einfriert". Das entspricht etwa der Größe eines Atoms. Die
Aufenthaltswahrscheinlichkeit geht gegen Null für einen Abstand gegen
Unendlich.
Dargestellt ist das 1s-Elektron. Das Wasserstoffatom
ist im Grundzustand. |
...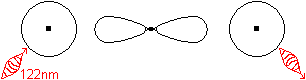 ... ... |
Die Lichtaussendung kann man sich so vorstellen.
Wird ein Atom durch Aufnahme einer passenden Energie
angeregt, so erreicht es einen energiereicheren Zustand und nimmt die Form
einer Keule an (2p-Elektron). Es ist nicht stabil und sendet ein Photon
aus. Danach nimmt es wieder die Grundform an. |
Welche fantastischen Formen angeregte Atome haben können,
findet man in der Galerie der Abteilung für Didaktik der Physik der
Universität Karlsruhe (URL unten).
Energieniveauschema
... ... ... |
Will man die Lichtaussendung eines Wasserstoffatoms studieren,
so ist das Orbitalmodell wenig hilfreich.
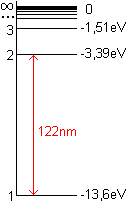
Da geht man besser vom Energieniveauschema aus, das aus
Rechnungen der Quantentheorie gewonnen wird. Es beschreibt die verschiedenen
Energiezustände, die ein Wasserstoffatom annehmen kann, durch horizontale
Linien. Energieaufnahme und Lichtabgabe sind dann wieder durch "Sprünge"
(nicht Elektronensprünge) zu erklären.
In dieser Betrachtungsweise wird das Bild der Kugel aufgegeben. |
Ergebnis:
"Sind Atome Kugeln?" kann man also nicht so einfach mit ja oder nein beantworten.
Schwimmende Kugel top
Wirft man eine Holzkugel ins Wasser, so hat man eine
"schwimmende Kugel". Der Frage, wie tief sie sinkt, wird auf einer Seite
von Matheplanet (URL unten) nachgegangen.
Hier geht es um andere schwimmende
Kugeln.
... ... ... |
Unter diesem Namen ist eine eindrucksvolle, weil leicht
bewegliche Steinkugel bekannt geworden. Obwohl die Kugel über eine
Tonne wiegt, lässt sie sich kinderleicht mit den Händen drehen.
Sie liegt in einer Mulde und schwebt sozusagen auf Wasser.
Ich sah die Kugel zum ersten Male im Sommer 1989 in Velden
am Wörther See vor dem Spielcasino, später in Hameln.
Heute findet man eine Miniaturausgabe sogar öfter
in Blumenläden fürs Zimmer. Aber wer will sie da schon haben? |
Aufgabe
Es bietet sich die Frage an: Wie
groß muss der Wasserdruck sein, um die Kugel zu halten?
Gegebene Daten:
Nach dem Foto ist der Durchmesser der Steinkugel etwa
2R=1m, der Durchmesser des Eintauch-Kreises etwa 2r=0,5m. Das Material
ist Granit.
Gegeben: R=0,5m, r=0,25m, d=2,7g/cm³=2700kg/m³
(Granit), g=9,81m/s² (Erdbeschleunigung), 10000Pa=1bar
Rechnungen
Größen: V Volumen der Kugel, m Masse der Kugel,
F Gewichtskraft der Kugel, p Druck des Wassers
V=(4/3)*pi*R³=(4/3)*pi*0,5³=0,524 m³
m=dV=2700(kg/m³)*0,524m³=1410kg=1,41 t
F=mg=1410kg*9,81m/s²=13800 N
A=pi*r²=pi*0,25²m²=0,196 m²
p=F/A=13800N/0,196m²=70400N/m²=70400Pa=0,704
bar
(Die allgemeine Formel für den Druck ist p=(4/3)dR³g/r².)
Ergebnis
Es muss nur ein Druck von etwa 0,7 bar aufgebracht werden,
um die Kugel zu halten.
Zum Vergleich: Wasser steht in der Wasserleitung unter
einem Druck von der Größenordnung 3 bar.
Pendelkette top
... ... ... |
Die Pendelkette ist ein physikalisches Spielzeug aus
fünf gleichartigen mathematischen Pendeln.
Fünf Kugeln hängen in einem Metallrahmen. Sie
sind bifilar aufgehängt und berühren sich.
Man kann alle Kugel gleichzeitig auslenken und dann loslassen.
Sie schwingen dann im Takt.
|
Der Aha-Effekt aber liegt
im folgenden Vorgang.
...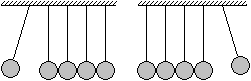 ... ... |
Lenkt man nur den Pendelkörper links aus und lässt
ihn los, so stößt er auf die Kette und gibt ihr einen Impuls.
Dieser pflanzt sich in der Kette fort. Die Pendel bleiben in Ruhe bis auf
den rechten Pendelkörper. Er bewegt sich nach außen. Er fällt
wieder zurück auf die Kette und lässt das linke Pendel ausschlagen.
Dieser Vorgang wiederholt sich mehrere Male.
[Eine Animation ist bei Wikipedia auf der Seite Stoß
(Physik)] |
Erste
Variante
...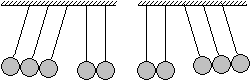 ... ... |
Es kommt noch schöner:
Lenkt man z.B. drei Pendel links aus, so fallen sie auf
die beiden übrigen. Überraschenderweise werden auch rechts drei
Pendel ausgelenkt. |
Zweite
Variante
... ... ... |
In diesen Zusammenhang passt der folgende Trick.
Man lässt einen großen Gummiball und einen
Tischtennisball gleichzeitig fallen. Nach dem Aufschlagen benimmt sich
der rote Ball wie erwartet, aber der kleine Ball saust in hohem Bogen davon.
Der Tischtennisball erhält einen Impuls mv.
Wegen seiner relativ kleinen Masse ist seine Geschwindigkeit
v groß. |
Dritte
Variante
... ... ... |
Eine Kugel rollt auf eine gleichartige Kugel zu und stößt
mit ihr zusammen. Man beobachtet, dass sie dann langsamer weiter rollt
und dass die vorher ruhende Kugel sich in Bewegung setzt. - Wie groß
sind die Geschwindigkeiten u1 und u2
nach dem Stoß? |
Eine Kugel
über Bad Salzuflen top
... ... ... |
Seit einigen Jahren gehört zur Silhouette der Stadt
ein Mast für den Mobilfunk, bei dem die Antennen unter einer Kugelhülle
verborgen sind.
Die Katze auf der Oberfläche ist ein Überbleibsel
der einst weltberühmten, heimischen "Hoffmann's Stärkefabriken".
Die Firma nahm eine typische Entwicklung.
>Ein ausländischer Konzern kaufte sie auf.
>Die Produktion lief einige Jahre weiter.
>Die Firma übersiedelte nach Hamburg.
>Das Gelände ist jetzt ein Ort für Supermärkte. |
Weitere
Kugeln auf meiner Homepage top
Fußball als Kugel
...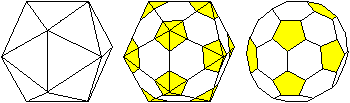 ... ... |
Schneidet man von einem Ikosaeder passend die Ecken ab,
entsteht ein
abgestumpftes Ikosaeder mit 12
regelmäßigen Fünfecken und 20 Sechsecken.
Zahlreiche Spielbälle haben diese Form. |
Weitere
Umkugeln bzw. Inkugeln findet man auf meinen Seiten Tetraeder,
Würfel,
Oktaeder,
Pentagondodekaeder,
Ikosaeder,
Kuboktaeder
und Rhombendodekaeder.
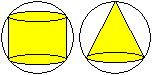
Zylinder
und Kegel in der Kugel
|
Über den größten Zylinder
und den größten
Kegel in der Kugel findet
man an anderen Stellen Untersuchungen. |
Puzzles
in Kugelform
... ... ... |
... ... ... |
Es gibt zahlreiche Puzzles in Kugelform.
Man kann meist diese Kugeln leicht zerlegen und muss sie
dann mühsam aus den Bestandteilen wieder zusammensetzen.
Zwei Beispiele findet man auf unter Zerlegbare
Kugeln. |
Kugeln im Internet
top
Deutsch
Abteilung für Didaktik der Physik, Universität
Karlsruhe
Das
Wasserstoffatom im Bild
Kusser Aicha Granitwerke
Weltgrößte
Schwimmende Kugel
Randolf Rehfeld
Kugelstoßpendel
Matheplanet
Wie
tief taucht eine schwimmende Kugel ein?
Wikipedia
Kugel,
Sphäre
(Mathematik), Kugeldreieck,
Kartenprojektion,
Stoß
(Physik), Kugelstoßpendel,
Modell,
Atom,
Bohrsches
Atommodell,
Teilchenmodell,
Orbital,
Wasserstoffatom
Englisch
Donald Simanek
Newton's
Cradle
Eric W. Weisstein (MathWorld)
Sphere,
Hypersphere
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Sphere,
Ball
(mathematics),
Spherical
cap, Map projection,
Atomic
orbital,
Newton's
cradle
Referenzen top
(1) Grimsehls Lehrbuch der Physik für höhere
Lehranstalten Teil 2, Stuttgart 1950
(2) A.Kleyer: Lehrbuch der Körperberechnungen, Stuttgart
1886
(3) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
(4) W.Gellert (Herausgeber u.a.): Kleine Enzyklopädie
Mathematik, Leipzig 1986
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |
 ...
...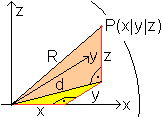 ...
...


 ...
... ......
...... ...
...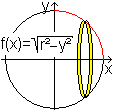 ...
... ...
... ...
...

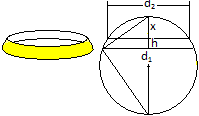



 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
...