Kugelteile
Inhalt dieser Seite
Was sind Kugelteile?
Kugelabschnitt
Die übrigen Kugelteile		 Zusammenfassung
Kugelteile im Internet
Referenzen.
Zur Hauptseite    "Mathematische Basteleien"

Was sind Kugelteile?
Legt man durch eine Kugel unterschiedliche Schnittflächen, entstehen Kugelteile. 
Einfache Kugelteile sind

Die Namen beschreiben sie treffend.

Der Kugelabschnitt heißt auch Kugelsegment, der Kugelausschnitt Kugelsektor und der Kugelkeil Kugelzweieck.
Meint man nur die gekrümmten Flächen, so heißen sie Kugelkappe oder Kugelkalotte beim Kugelabschnitt, Kugelzone bei der Kugelschicht.
Blick in ein altes Lehrbuch
Die sechs Kugelteile entdeckt man schon in einem Lehrbuch von 1886. 

Kugelabschnitt  top
 
...... Legt man durch eine Kugel eine Ebene, so wird sie in zwei Kugelabschnitte aufgeteilt. 

...... Der obere Kugelabschnitt z.B. wird durch den Radius r der Kugel, den Radius a des Grundkreises und der Höhe h bestimmt. Es genügen offenbar zwei dieser drei Längen, um den Kugelabschnitt festzulegen. 
...... Einen Zusammenhang zwischen den drei Längen gibt der Satz des Pythagoras an: 
(r-h)²+a² = r² oder h²-2rh+a² = 0.
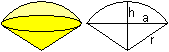
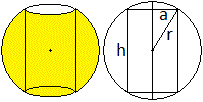
Größen des Kugelabschnitts
Neben den drei Größen r, h und a gibt es das Volumen V, den Mantel M und die Oberfläche O.
Es gelten, wenn r und h gegeben sind, folgende Formeln.
 
a = sqrt(2rh-h²) V = (1/3)pi*h²(3r-h) M = 2pi*rh O = pi*(4rh-h²)

Herleitungen
Radius a des Grundkreises
Sind der Radius r und die Höhe h gegeben, so gilt (r-h)²+a² = r². Daraus folgt a = sqrt(2rh-h²). 
Die zweite Lösung a = -sqrt(2rh-h²) ist negativ und deshalb unbrauchbar.

Volumen V
Es wird eine Formel angewandt, die das Volumen eines Körpers beschreibt, der entsteht, wenn man den Graphen zu y=f(x) um die x-Achse rotieren lässt.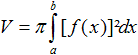
......
Aus der Kreisgleichung x²+y²=r² ergibt sich der Funktionsterm f(x) = sqrt(r²-x²). Das Intetgral ist dann 
Die Stammfunktion zum Integral ist F(x) =pi*[(r²x-(1/3)x³]. 
Das Volumen ist dann V = pi*[F(r)-F(r-h)] = pi*[r³-(1/3)r³]-pi*[r²(r-h)-(1/3)(r-h)³] = ... = pi*[rh²-(1/3)h³] = (1/3)pi*h²(3r-h).
Mantel M
Es wird eine Formel angewandt, die die Oberfläche eines Körpers beschreibt, der entsteht, wenn man den Graphen zu y=f(x) um die x-Achse rotieren lässt.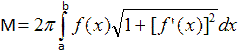

...... Man setzt wieder f(x) = sqrt(r²-x²). 
Dann ist f '(x) = -x/sqrt(r²-x²) und f'²(x) = x²/(r²-x²) und 1+f'²(x) = r²/(r²+x²) und sqrt[1+f '²(x)] = r/sqrt(r²-x²).
Schließlich ist f(x)sqrt[1+f '²(x)] = r.
Das führt zu 
Oberfläche O
Zur Bestimmung der Oberfläche muss man noch den Flächenhalt des Grundkreises addieren. 
O = 2pi*rh+pi*a² = 2pi*rh+pi*(2rh-h²) = pi*(4rh-h²)
Zweite Formel für das Volumen
Herleitung
Sind der Radius a des Grundkreises und die Höhe h gegeben, so lautet die Formel V = pi*h[(1/2)a²+(1/6)h²].
Herleitung
...... Nach dem Satz des Pythagoras gilt r² = (r-h)²+a² oder r = (1/2)a²/h+(1/2)h.
Dann ist V = (1/3)pi*h²(3r-h) = pi*h²r-(1/3)pi*h³ = pi*h²(1/2)a²/h+(1/2)h-(1/3)pi*h³ = ... = pi*h[(1/2)a²+(1/6)h²].
Führt man den Durchmesser d = 2a ein, so gilt V = pi*h[(1/8)d²+(1/6)h²].
Halbkugel
Ist a=r, so entsteht eine Halbkugel. Über sie habe ich eine Webseite gemacht.

Die übrigen Kugelteile      top
Kugelausschnitt
...... Legt man in eine Kugel einen Kegel, so dass seine Spitze im Mittelpunkt der Kugel liegt, so schneidet er einen Kugelausschnitt aus. Dieser setzt sich aus einem Kegel und einem Kugelabschitt zusammen.

Volumen
V =(1/3)pi*h²(3r-h)+(1/3)pi*a²(r-h) =  (1/3)pi*h²(3r-h)+(1/3)pi*(2rh-h²)(r-h) = ... = (2/3)pi*r²h
Oberfläche
O = 2pi*rh+pi*ra = pi*r(a+2h)
 Kugelschicht
...... Legt man durch eine Kugel zwei parallele Ebenen, so liegt zwischen ihnen eine Kugelschicht. Sie ist der Differenzkörper zweier Kugelabschnitte. 
Volumen 
V = (1/24)pi*h(3d1²+3d2²+4h²) 
Herleitung 
Die Formel des Kugelabschnitts V =  pi*h[(1/8)d²+(1/6)h²] von oben wird angewandt. Der Durchmesser der Kugel ist d=2r.
V = V1-V2
V1 = pi*(h+x)[(1/8)d1²+(1/6)(h+x)²] = ... = (1/24)pi*(3d1²h+4h³+12h²x++12hx²+3d1²x+4x²)
V2 = pi*x[(1/8)d2²+(1/6)x²] = ... = (1/24)pi*[3d2²x+4x²]
V = V1-V2 = (1/24)pi*(3d1²h+4h³+12h²x+12hx²+3d1²x+4x²-3d2²x-4x²)
Nach dem Höhensatz gilt [(1/2)d1]²=(h+x)[d-(h+x)]. Dann ist d1² = 4(h+x)[(d-x)-h)]
Nach dem Höhensatz gilt [(1/2)d2]²=x(d-x). 
Das sind zwei Gleichungen, mit deren Hilfe die Variablen d und x eliminiert werden müssen. 
Aus der ersten Gleichung folgt d1² = 4(h+x)[(d-x)-h)].
Aus der zweiten Gleichung folgt d-x = d2²/(4x).
Dann eliminiert man d:
d1² = 4(h+x)[(d-x)-h)] oder d1² = 4(h+x)[d2²/(4x)-h)] und ausmultipliziert d1²x = d2²h-4h²x+d2²x-4hx².
Aus dieser Gleichung müsste man x berechnen und in den Volumen-Term einsetzen. Das scheitert an der quadratischen Gleichung.
Aber nach einer Idee aus dem Kusch schafft man es x zu eliminieren:
Aus d1²x = d2²h-4h²x+d2²x-4hx² geht d2²h = d1²x+4h²x-d2²x+4hx² hervor.
d2²h = x(d1²+4h²-d2²+4hx)
3d2²h = 3x(4h²+4hx+d1²-d2²)
Für das Volumen gilt 
V = (1/24)pi*(3d1²h+4h³+12h²x+12hx²+3d1²x+4x²-3d2²x-4x²) oder
V = (1/24)pi*[3d1²h+4h³+3x(4h²+4hx+d1²-d2²)] oder
V = (1/24)pi*(3d1²h+4h³+3d2²h) oder
V = (1/24)pi*h(3d1²++3d2²+4h²)
Bemerkenswert ist, dass das Volumen nicht vom Durchmesser bzw. Radius der Kugel abhängt, sondern von den Radien des Deck- und Grundkreises und der Dicke der Schicht.
Mantel
M = 2pi*rh1-2pi*rh2 = 2pi*r(h1-h2) = 2pi*rh 
Kugelkeil
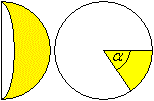
...... Legt man durch eine Kugel zwei Ebenen, deren Schnittgerade durch den Kugelmittelpunkt geht, so schneiden sie einen Kugelkeil aus. Offenbar sind das Volumen und der Mantel proportional zum Winkel alpha.
Volumen
Es gilt V:alpha = Vkugel:360°. Dann ist V = (alpha/360°)(4/3)pi*r³ = (4/3)pi*r³*(alpha/360°).
Mantel
Es gilt M:alpha = Okugel:360°. Dann ist M=4pi*r²(alpha/360°).
Kugelring
...... Legt man in eine Kugel einen Zylinder, dessen Achse durch den Kugelmittelpunkt geht, so entsteht ein Kugelring. Das entfernte Kugelstück ist ein Zylinder mit zwei aufgesetzten Kugelabschnitten. 
Volumen
V = VKugelschicht -VZylinder
= (1/24)pi*h(3d1²+3d2²+4h²)-pi*a²h = (1/24)pi*h(12a²+12a²)+(1/6)pi*h³-pi*a²h = pi*a²h+(1/6)pi*h³-pi*a²h = (1/6)pi*h³ 
Oberfläche
O = MKugelschicht+MZylinder = 2pi*rh+2pi*ah = 2pi*h(r+a)
Anmerkung
Bemerkenswert ist, dass das Volumen des Kugelrings nur von der Höhe des ausgeschnittenen Zylinders abhängt ("Napkin ring problem", s.u.).
Hohlkugel
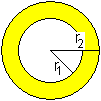
...... Legt man in eine Kugel konzentrisch eine kleinere Kugel, so entsteht eine Hohlkugel. 
Volumen
V = (4/3)pi*(r2³-r1³)
Begrenzungsflächen
O = 4pi*(r1²+r2²)

Zusammenfassung top
Kugelabschnitt oder Kugelsegment
Gelb: Kugelkappe, -haube, -kalotte

V=(1/3)*pi*h²(3r-h)= pi*h[(1/2)a²+(1/6)h²]
M=2pi*rh
O=pi*(a²+2rh) 
Kugelausschnitt oder Kugelsektor
.

V=(2/3)*pi*r²h
O=pi*r(2h+a)		 Kugelschicht,  Gelb: Kugelzone

V= (1/24)pi*h(3d1²++3d2²+4h²)
M=2pi*rh
Kugelkeil
gelb: Kugelzweieck (M)

V=(4/3)pi*r³(alpha/360°)
M=4pi*r²(alpha/360°)

 Kugelring

V= (1/6)pi*h³ 
O = 2pi*h(r+a)

 Hohlkugel

V = (4/3)pi*(r2³-r1³)
O = 4pi*(r1²+r2²)
Perlen mit einer Bohrung sind Kugelringe.

Kugelteile im Internet      top

Deutsch

Jürgen Kummer (rechneronline.de)
Kugelsegment-Rechner (u.a.)

Wikipedia 
Kugel, Kugelsegment, Kugelausschnitt, Kugelschicht, Kugelring, Kugelkeil

Englisch

Eric W. Weisstein  (MathWorld)
Sphere, Spherical Cap, Spherical Lune, Spherical Segment,  Spherical Ring, 
Spherical Wedge,  Zone, Archimedes' Hat-Box Theorem,  Hemisphere

Wikipedia 
Sphere, Spherical cap,  Spherical sector,  Spherical segment, Napkin ring problem,  Spherical wedge, Spherical shell, 
Napkin ring problem

Referenzen   top
(1) A.Kleyer: Lehrbuch der Körperberechnungen, Stuttgart 1886
(2) Richard Dörfling: Mathematik für Ingenieure und Techniker, München 1965
(3) Lothar Kusch: Mathematik für Schule und Beruf, Teil 2, Essen 1971 [ISBN 3 7736 2582 0] 
(4) Bronstein-Semendjajew: Taschenbuch der Mathematik. Harri-Deutsch-Verlag, 1983, [ISBN 3-87144-492-8]

 Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  November 2016 Jürgen Köller

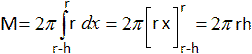
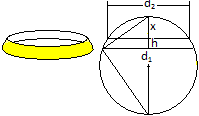top