|
Was ist das Ikosaeder?
...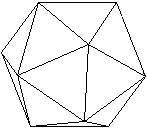 .... .... |
Das Ikosaeder ist der Körper, der von 20 gleichseitigen
Dreiecken gebildet wird.
Ikosaeder heißt Zwanzig-Flächner.
|
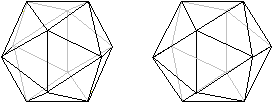
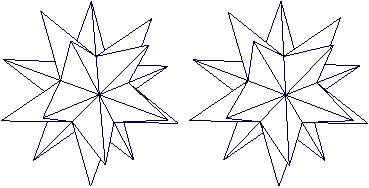
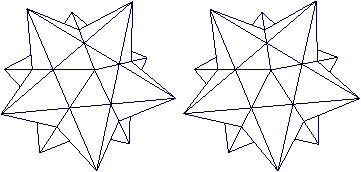
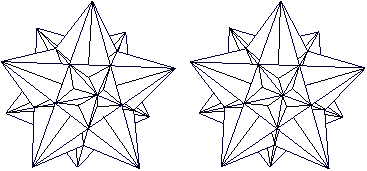
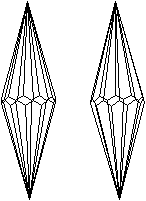
Die folgenden Bildpaare ermöglichen
eine dreidimensionale Sicht.
.
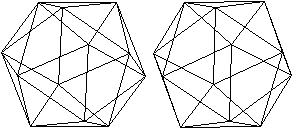
durchsichtig durchsichtig
|
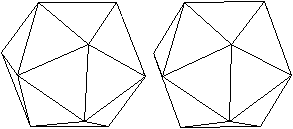
undurchsichtig undurchsichtig
|
Das Ikosaeder wird nur von
gleichseitigen Dreiecken begrenzt und ist somit auch ein
Deltaeder.
Kommt man vom Namen Ikosaeder
oder Zwanzig-Flächner her, so
müsste jeder Körper mit 20 Flächen diesen Namen tragen.
So müsste das Ikosaeder von oben näher gekennzeichnet werden,
etwa in Anlehnung an das Pentagondodekaeder als Trigonikosaeder
(auch im Internet nicht gefunden) oder als regelmäßiges Ikosaeder
(selten verwendet). Offenbar verzichtet man auf eine nähere Beschreibung.
Langer Rede kurzer Sinn: Das Ikosaeder ist gemeinhin
der platonische Körper.
Beschreibungen top
Daten
Das Ikosaeder hat neben f=20 Seitenflächen noch
k=30 Kanten und e=12 Ecken.
Es gilt der eulersche Polyedersatz e+f=k+2.
In jedem Eckpunkt treffen fünf Kanten bzw. fünf
Flächen aufeinander.
Aufbau
Jede Ecke bildet die Spitze einer fünfseitigen Pyramide.
...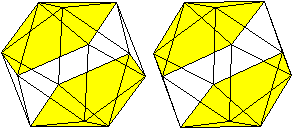 ... ... |
Je zwei Pyramiden stehen entgegengesetzt einander gegenüber.
Dabei sind die Grundflächen gegeneinander gedreht. |
...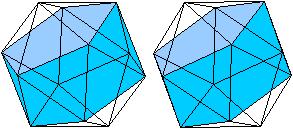 ... ... |
Zwischen den Pyramiden liegt eine Schicht, gebildet aus
zwei Fünfecken und zehn gleichseitigen Dreiecken.
Der Schichtkörper ist ein fünfseitiges Antiprisma,
das dadurch entsteht, dass man die Ecken der Fünfecke durch eine Zickzacklinie
miteinander verbindet. |
Anzahl
der Raumdiagonalen
...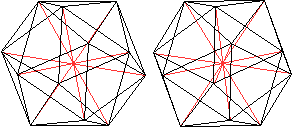 ... ... |
Verbindet man die 12 gegenüberliegenden Eckpunkte,
entstehen 6 Raumdiagonalen.
Sie legen den Mittelpunkt des Ikosaeders fest. |
Dann gibt es noch kürzere
Raumdiagonalen.
...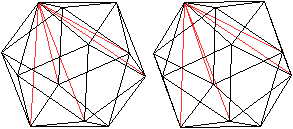 ... ... |
Von einem Punkt gehen immer 5 Diagonalen aus.
Da es 12 Ecken gibt, ergibt das 5*12=60 Diagonalen.
Dabei wird jede Diagonale doppelt gezählt.
Es gibt also 30 Raumdiagonalen dieser Art. |
Auf die Anzahl 6+30=36 Raumdiagonalen
kommt man auch auf einem anderen Weg.
Das Ikosaeder hat 12 Eckpunkte. Verbindet man alle Punkte,
so erhält man "12 über 2" oder 66 Linien.
Die Anzahl der Raumdiagonalen ergibt sich, wenn man die
Anzahl der Kanten (30) abzieht.
Das ergibt 36 Linien.
Parallelprojektionen
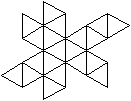
Netze
des Ikosaeders
|
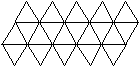
|
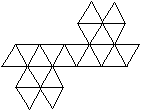
|
Das sind drei von 43380 Netzen. |
Schlegeldiagramm
...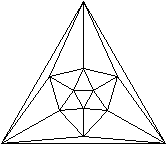 ... ... |
Das Schlegeldiagramm ist eine besondere Darstellung des
Ikosaeders in der Ebene.
Es stellt seine topologischen Eigenschaften dar, also
mehr die Beziehungen zwischen den Eckpunkten, Kanten und Flächen. |
Halbierungen
des Ikosaeders
...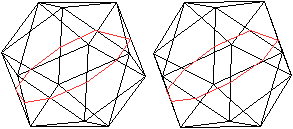 ... ... |
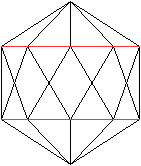
Verbindet man die Mittelpunkte von sechs passenden Kanten,
erhält man ein regelmäßiges Zehneck.
Eine Ebene durch das Zehneck halbiert das Ikosaeder. |
...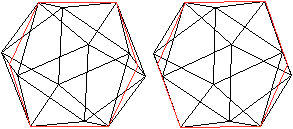 ... ... |
Diese Halbierung mit Hilfe von Kanten und Flächenhöhen
ermöglicht einen Zugang zu den Formeln des Ikosaeders (s.u.). |
Symmetrien top
Das Ikosaeder hat einen Mittelpunkt. Er ist das Symmetriezentrum.
...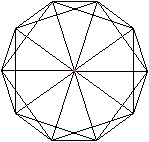 ... ... |
Schaut man auf eine Ecke des Ikosaeders, so stellt es
sich als eine fünfstrahlige, drehsymmetrische Figur dar. Diese Symmetrie
überträgt sich auf das Ikosaeder.
Die Drehachse zeigt sich in der Zeichnung als Punkt in
der Mitte. |
...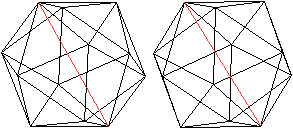 ... ... |
Es gibt 12 Eckpunkte und damit 6 Paare von gegenüberliegenden
Eckpunkten. Durch sie verlaufen die Drehachsen.
Es sind also die längeren Raumdiagonalen.
Links ein Beispiel |
...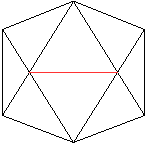 ... ... |
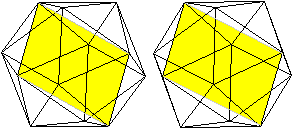
Schaut man so auf das Ikosaeder, dass zwei gegenüberliegende
Kanten zusammenfallen, ergibt sich die nebenstehende achsensymmetrische
Figur.
Auf das Ikosaeder übertragen heißt das, dass
eine Ebene durch diese Kanten Symmetrieebene ist.
|
... ... ... |
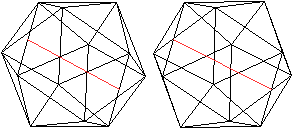
Es gibt 30 Kanten oder 15 Paare von Kanten.
In der linken Zeichnung wird die Symmetrie-Ebene durch
ein Rechteck gekennzeichnet.
Das ist ein Beispiel. |
... ... ... |
Verbindet man die Mittelpunkte gegenüberliegender
Kanten, so stehen sie für weitere 15 zweistrahlige Achsensymmetrien.
Links ein Beispiel |
...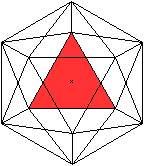 ... ... |
Schaut man auf ein Dreieck, so stellt sich das Ikosaeder
als eine dreistrahlige oder dreizählige, drehsymmetrische Figur dar.
Die Drehachse ist in der Zeichnung nur ein Punkt. |
...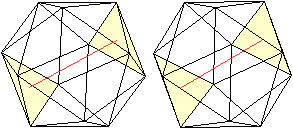 ... ... |
Da es 10 Paare von Dreiecken gibt, gibt es auch 10 Drehachsen.
Sie verlaufen durch die Mittelpunkte der Dreiecke.
Links ein Beispiel |
Umhüllender
Würfel top
...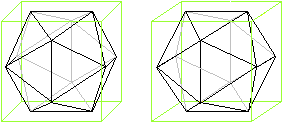 ... ... |
Es gibt einen (grünen) Würfel, den man um das
Ikosaeder legen kann.
Dabei berühren drei gegenüberliegende Kantenpaare
den Würfel in Mittellinien der Würfelflächen. |
...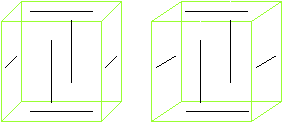 ... ... |
Der Deutlichkeit halber sind nur der Würfel und
die sechs Kanten gezeichnet. |
...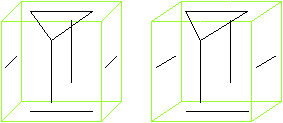 ... ... |
Man erhält das Ikosaeder, indem man Endpunkte von
Kanten passend miteinander verbindet.
Als Beispiel ist eine Seitenfläche eingezeichnet. |
Goldene
Rechtecke
... ... ... |
Verbindet man die Endpunkte der parallelen Kanten passend,
so entstehen drei orthogonale Rechtecke. |
...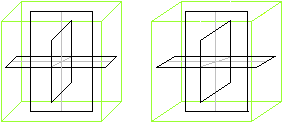 ... ... |
Es gilt dann, dass die Seiten der eingezeichneten Rechtecke
im Verhältnis des Goldenen Schnittes stehen.
Deshalb heißen die Rechtecke auch Goldene Rechtecke. |
Größen top
Das Ikosaeder hat die Kantenlänge a, das
Volumen
V, die Oberfläche O, den Radius R der
Umkugel, den Radius
r der Inkugel und den Radius rkder
Kantenkugel.
Ist die Kantenlänge a gegeben, so gilt für
die übrigen Größen:
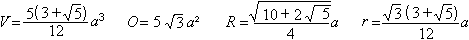
Herleitungen
... ... ...
|
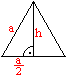
Man verwendet im Folgenden zwei Formeln des gleichseitigen
Dreiecks.
Höhe h = (1/2)sqrt(3)a
Flächeninhalt A3=(1/4)sqrt(3)a²
|
Oberfläche
O
O=20*A3=20*(1/4)sqrt(3)a²=5sqrt(3)a²
Radius
R der Umkugel und Radius r der Inkugel
... ... ... |
Man legt durch die Mitte des Körpers einen Schnittebene,
in der die Kugeln als Kreise erscheinen. |
...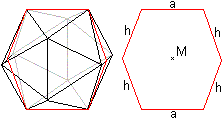 ... ... |
Die Schnittfläche ist ein Sechseck, das aus vier
Dreieckshöhen und zwei Kanten des Ikosaeders gebildet wird. |
...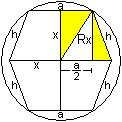 ... ... |
Den Radius der Umkugel bestimmt man, indem man nach dem
Satz des Pythagoras zunächst die Hilfsstrecke x bestimmt:
h²=x²+(x-a/2)². Die quadratische Gleichung
wird vereinfacht zu x²-(a/2)x-a²/4=0. Die zutreffende Lösung
ist x=(1/4)[1+sqrt(5)]a.
Dann folgt nach dem Satz des Pythagoras R²=a²/4+x²
oder R=(1/4)sqrt[10+2sqrt(5)]a. |
...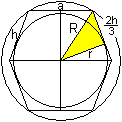 ... ... |
Den Radius der Inkugel bestimmt man, indem man nach dem
Satz des Pythagoras die Gleichung R²=r²+(2h/3)²=r²+a²/3
aufstellt.
Es ergibt sich r²=R²-a²/3=42/144*a²+18sqrt(5)/144*a²
und r=(1/12)sqrt(3)[3+sqrt(5)]a.
Dabei verwendet man die Identität sqrt[14+6sqrt(5)]=3+sqrt(5). |
Radius
der Kantenkugel
Die Kantenkugel ist die Kugel durch alle Kantenmitten.
... ... ... |
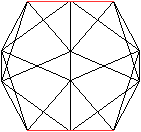
Man erhält den Radius, indem man ein Zehneck des
Ikosaeders, das es halbiert, betrachtet und dann den Umkreis des Zehnecks.
Dessen Radius ist der Radius der Kantenkugel. |
...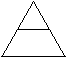 ... ... |
Der Radius ist die Mittellinie eines gleichseitigen Dreiecks.
Für sie gilt s = (1/2)a. - Der Radius des Umfangskreises
eines Zehnecks ist (1/2)[1+sqrt(5)s.
Damit ist auch der Radius der Umkugel rk =
(1/4)[1+sqrt(5)]a. |
Volumen
V

Die sechs Hauptdiagonalen zerlegen das Ikosaeder in 20
dreiseitige Pyramiden.
Eine Pyramide hat die Grundfläche A3
und die Höhe r.
Es gilt V=20*[(1/3)A3*r]= 20*(1/4)sqrt(3)a²*(1/3)(1/12)sqrt(3)[3+sqrt(5)]a=...=(5/12)[3+sqrt(5)]a³.
Winkel
zwischen zwei Seitenflächen
...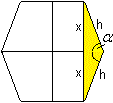 ... ... |
Der Winkel zwischen zwei Seitenflächen
taucht
im unregelmäßigen Sechseck oben auf und zwar zwischen den Höhen
des markierten Dreiecks. Für den Winkel alpha gilt nach dem Kosinussatz
(2x)² = h²+h²-2h²cos(alpha).
Daraus folgt cos(alpha) = (2h²-4x²)/(2h²).
Setzt man h = (1/2)sqrt(3)a und x = (1/4)[1+sqrt(5)]a
ein, so ergibt sich cos(alpha) = -(1/3)sqrt(5). |
Dann ist der Winkel zwischen zwei Seitenflächen gerundet
alpha =138,2°.
Winkel
zwischen Kante und Seitenfläche
...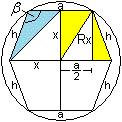 ... ... |
Im Sechseck tritt auch der Winkel beta zwischen einer
Kante a und der Höhe h einer Dreieckfläche auf.
Das markierte Dreieck hat die Seiten sqrt(2)x, (1/2)a
und h.
Nach dem Kosinussatz gilt 2x² = (1/4)a²+h²-2*(1/2)ah*cos(beta).
Daraus folgt cos(beta) = (a²+4h²-8x²)/(4ah).
Setzt man h = (1/2)sqrt(3)a und x = (1/4)[1+sqrt(5)]a
ein und vereinfacht, so ist cos(beta) = -(1/6)[sqrt(15)-sqrt(3)].
Das führt gerundet zu beta = 110,9°. |
Probe
Im Sechseck treten die Winkel alpha zweimal und die Winkel
beta viermal auf.
Dann ist 2*alpha+4*beta = 2*138.2+4*110,9 = 720°.
Das ist die Winkelsumme im Sechseck.
Ikosaeder
und Pentagondodekaeder top
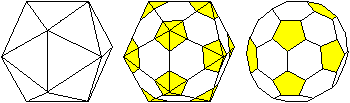
Vom Ikosaeder zum Pentagondodekaeder
und zurück
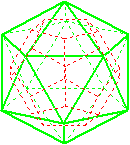
Verbindet man die Mittelpunkte der Seitendreiecke
eines Ikosaeders, entsteht ein Dodekaeder.
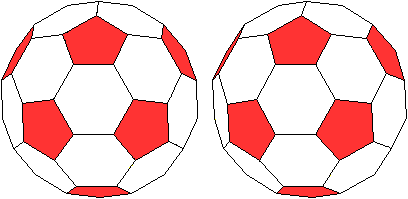
|
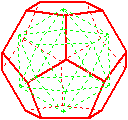
.Verbindet man die Mittelpunkte
der Seitenfünfecke
eines Dodekaeders, entsteht ein Ikosaeder.
|
Die beiden Zeichnungen stellte
mir Christian Grünwaldner zur Verfügung.
Ikosaeder und Pentagondodekaeder
sind also duale Körper.
Dann gibt es folgende Beziehungen.
>Der Ikosaeder hat 12 Ecken, 30
Kanten und 20 Flächen.
>Vertauscht man die Zahlen 12 und
20 und behält 30 bei, so erhält man die Daten des Pentagondodekaeders.
>Das Pentagondodekaeder hat 20
Ecken, 30 Kanten und 12 Flächen.
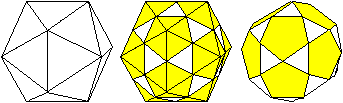
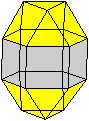
Rhombentriadodekaeder
Das Rhombentriadodekaeder ist ein
konvexer Körper aus 30 kongruenten Rhomben.
Es hat außerdem 32 Eckpunkte
und 60 Kanten. Es ist der duale Körper des
Ikosidodekaeders.
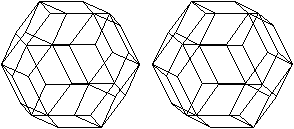
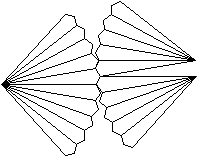
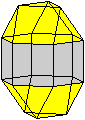
durchsichtig
durchsichtig
|
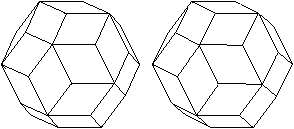
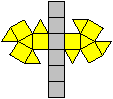
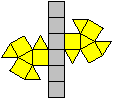
undurchsichtig undurchsichtig
|
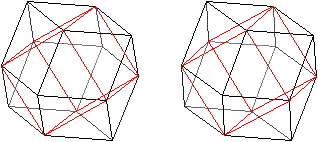
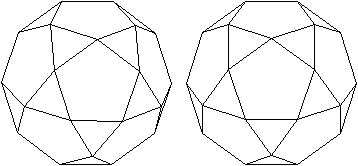
Das ist das Besondere.
...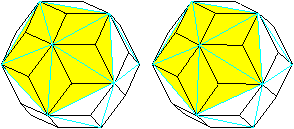 ... ... |
Verbindet man gewisse Eckpunkte, entsteht ein Ikosaeder.
In der Zeichnung ist das nur angedeutet. |
...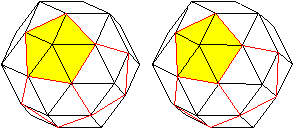 ... ...
|
Verbindet man andere Eckpunkte, entsteht ein Pentagondodekaeder.
In der Zeichnung ist das nur angedeutet. |
Das
Rhombentriadodekaeder ist also ein Körper, der sowohl ein Ikosaeder
als auch ein Dodekaeder enthält. Es ist der Hüllkörper des
Körpers aus beiden.
...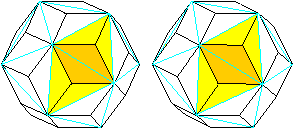 ... ... |
Es gibt auch eine zweite Annäherung an das Rhombentriadodekaeder.
Man gibt ein Ikosaeder vor und
setzt auf die Seitenflächen dreieckige Pyramiden. Man wählt die
Höhe der Pyramiden so, dass anstoßende Seitenflächen einen
Rhombus bilden. |
Vom
Ikosaeder zu weiteren Körpern top
Vom Ikosaeder zum dreiseitigen
Antiprisma
...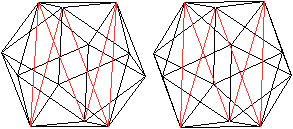 ... ... |
Je zwei Dreiecke liegen sich gegenüber und sind
parallel.
Verbindet man sie mit einer Zickzacklinie, so entsteht
ein dreiseitiges Antiprisma. |
Vom
Ikosaeder zum Abgestumpften Ikosaeder
Mehr auf meiner Webseite Abgestumpftes
Ikosaeder
Vom
Ikosaeder zum Ikosidodekaeder
Mehr auf meiner Webseite Ikosidodekaeder
Vom
Ikosaeder zum Großen Sterndodekaeder
Mehr auf meiner Webseite Kepler-Poinsot-Körper
Vom
Großen Sterndodekaeder zum Großen Ikosaeder
Mehr auf meiner Webseite Kepler-Poinsot-Körper
Oktaeder im
Ikosaeder
...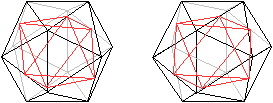 ... ... |
Verbindet man sechs bestimmte Mittelpunkte von Kanten
des Ikosaeders, so entsteht ein Oktaeder.
Es gibt fünf Möglichkeiten, ein Oktaeder in
das Ikosaeder zu legen. |
Zeichnet man alle Oktaeder ein, so entsteht ein Sternkörper.
Er ist auf der Webseite von MathWorld (URL unten) unter
"Octahedron 5-Compound" dargestellt.
Für den
Fall Tetraeder
im Pentagondodekaeder beschreibe ich ausführlich die Entstehung
eines ähnlichen Sterns.
Fünf
Johnson-Körper
Johnson-Körper
sind konvexe Körper aus regelmäßigen Vielecken.
Fünf (von 92) entstehen aus einem Ikosaeder.
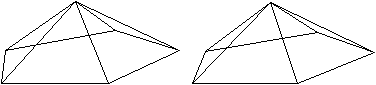
J 02 Fünfeckpyramide
... ... ... |
... ... ... |
Der Körper entsteht auch dadurch, dass man
eine Fünfeckpyramide des Ikosaeders isoliert. |
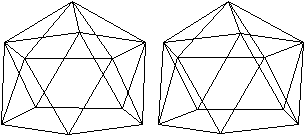
J11 Beschnittenes Ikosaeder
... ... ... |
...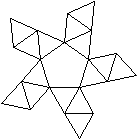 ... ... |
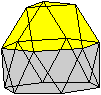
Der Körper entsteht, indem man vom Ikosaeder eine
Fünfeckpyramide (unten) entfernt. |
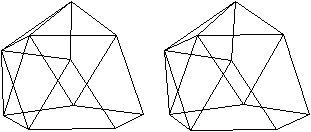
J 62 Doppelt beschnittenes
Ikosaeder
... .. .. |
...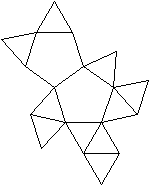 ... ... |
Das Ikosaeder enthält innen 12 Fünfecke.
Man beschneidet es so, dass zwei Fünfecke außen
liegen. |
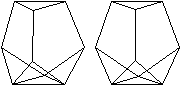
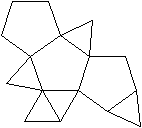
J 63 Dreifach beschnittenes
Ikosaeder
... ... ... |
... ...
... |
Das Ikosaeder enthält innen 12 Fünfecke.
Man beschneidet es so, dass drei Fünfecke außen
liegen. |
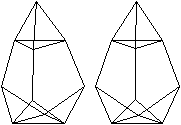
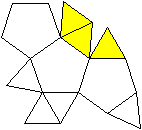
J 64 Erweitertes dreifach
beschnittenes Ikosaeder
.. .... .... |
... ... ...
|
Auf das dreifach beschnittene Ikosaeder J 63 wird ein
Tetraeder gesetzt. |
Zwanzig-Flächner
top
Ein Ikosaeder ist ein Zwanzg-Flächner.
Es folgt die Aufzählung einiger Körper, die
auch von 20 Vielecken gebildet werden.
20-seitiges
Trapezoeder
Mehr über Trapezoeder findet man auf meiner Webseite
Bipyramiden.
Es folgen sechs Johnson-Körper.
J 22 Verdreht verlängerte
Dreieckskuppel
|
J 35 Verlängerte
Dreiecksdoppelkuppel
|
J 36 Verlängerte verdrehte
Dreiecksdoppelkuppel
|
Mehr über diese Kuppeln findet man auf meiner Webseite
Johnson-Körper.
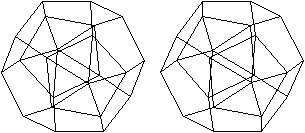
J59 Doppelt erweitertes Dodekaeder (para)
... ... ...
|
...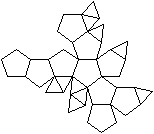 ... ... |
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf zwei gegenüberliegende Seitenflächen wird
eine fünfseitige Pyramide gesetzt. |
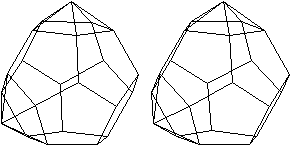
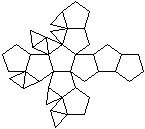
J60 Doppelt erweitertes Dodekaeder
(meta)
... ... ...
|
... ... ...
|
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf zwei nicht gegenüberliegende Seitenflächen
wird eine fünfseitige Pyramide gesetzt. |
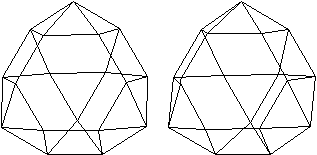
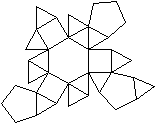
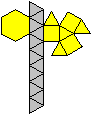
J 92 Dreieckshebosphenorotunde
... ... ...
|
... ... ...
|
Der Körper besteht aus einem Sechseck, drei Fünfecken,
drei Quadraten und 13 gleichseitigen Dreiecken. |
Weitere Körper mit 20
Flächen findet man auf der Webseite Icosahedron von Mathworld
(URL unten).
Darunter sind z.B. die zehnseitige Bipyramide,
das achtzehnseitige Prisma, das neunseitige Antiprisma, das
große
Ikosaeder und das "Rhombic Icosahedron".
Ikosaeder im Internet
top
Deutsch
Gerd Müller
Platonische
Körper in Stereodarstellung
H. B. Meyer (Polyeder aus Flechtstreifen)
Ikosaeder
Walter Fendt
Das
Ikosaeder (.pdf-Datei)
Wikipedia
Ikosaeder
Englisch
Eric W. Weisstein (MathWorld)
Icosahedron,
Truncated
Icosahedron, Icosahedron
Stellations, Octahedron5-Compound,
Rhombic
Icosahedron
Kenneth James Michael MacLean
THE
ICOSAHEDRON
Poly
A program for downloading
(Poly is a shareware program for exploring and constructing polyhedra)
Die meisten Bilder dieser Seite wurden mit diesem
Programm erzeugt.
Robert Webb
Stella:
Polyhedron Navigator
Wikipedia
Icosahedron,
Rhombic
icosahedron,
Französisch
Robert FERRÉOL (MathCurve)
ICOSAÈDRE
Dank an Nicolas Kauffmann
aus Wuppertal für Unterstützung
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2004,
erweitert 2012, Jürgen Köller
top |

 ....
....


 ...
... ...
... ...
...





 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...



 ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ..
.. ...
... ...
... ...
... ....
.... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
...