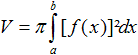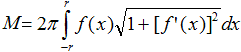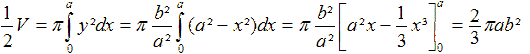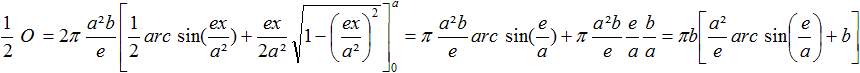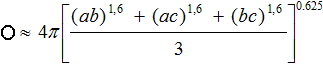|
Was ist ein Ellipsoid?
...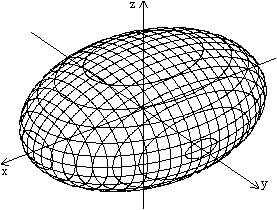 |
Ein Ellipsoid ist der Graph der Relation x²/a²+y²/b²+z²/c²=1.
Der größtmögliche Definitionsbereich
ist
D={(x, y, z)|-a<= x <=a, -b<= y <=b, -c<=
z <=c}
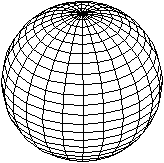
Es wird hier dargestellt im kartesischen Koordinatensystem.
Für die Zeichnung gilt x²/4+y²/2+z²/1=1.
|
...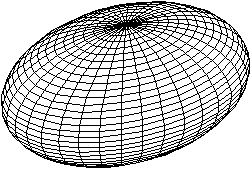 |
Das gleiche Ellipsoid hat die Parameterdarstellung
x=a*sin(u)cos(t)
y=b*sin(u)sin(t)
z=c*cos(u)
D={(t, u)|-2pi;<=t<=2pi, -pi<= u <= pi}
|
Es ist wirklich das gleiche Ellipsoid, wie die folgende
Rechnung zeigt.
Es gilt x²/a²+y²/b²+z²/c²
=[a*sin(u)cos(t)]²/a²+[b*sin(u)sin(t)]²/b²+[c*cos(u)]²/c²=sin²(u)cos²(t)+sin²(u)sin²(t)+cos²(u)=sin²(u)+cos²(u)=1.
Auf meiner Seite Torus
erkläre ich, wie man mit dem Programm Winplot Körper dieser Art
zeichnet.
...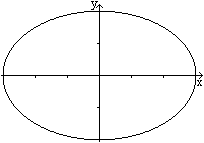 |
Das Ellipsoid ist die Verallgemeinerung der Ellipse
auf die dritte Dimension.
Diese ist der Graph der Relation x²/a²+y²/b²=1
mit D={(x, y)| -a<= x <=a, -b<= y <=b}. |
Bezeichnungen top
Setzt man in die Koordinatengleichung x²/a²+y²/b²+z²/c²=1
eine Koordinate gleich Null, so erhält man die drei Hauptellipsen
des Ellipsoids.
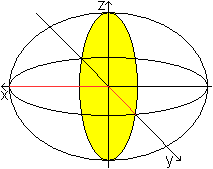
x=0 führt zur Ellipsengleichung y²/b²+z²/c²=1
bzgl. der y-z-Ebene
|
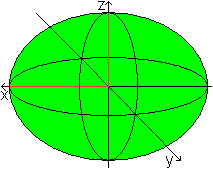
y=0 führt zur Ellipsengleichung x²/a²+z²/c²=1
bzgl. der x-z-Ebene
|
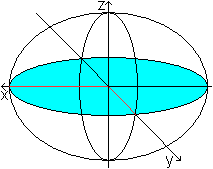
z=0 führt zur Ellipsengleichung x²/a²+y²/b²=1
bzgl. der x-y-Ebene
|
Übrigens führt
jeder ebene Schnitt durch das Ellipsoid zu einer Ellipse.
Das Ellipsoid ist symmetrisch
zu den Hauptebenen, da der Term der Relation sich nicht ändert, wenn
man x, y und z durch ihre Gegenzahlen -x, -y und -z ersetzt.
...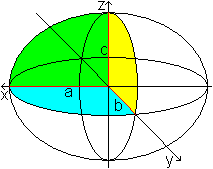 |
Die Halbmesser a, b und c der Hauptellipsen heißen
auch
Halbmesser des Ellipsoids.
Gilt a > b > c, so ist a der große,
b der
mittlere b und c der kleine Halbmesser.
Die Scheitel der Hauptellipsen heißen auch
Scheitel
des Ellipsoids. |
Eine Ellipsoid mit a > b
> c heißt dreiachsiges Ellipsoid.
Rotationsellipsoide
top
Eine besondere Rolle spielen Ellipsoide, bei denen zwei
von drei Halbmessern gleich sind. Es sei z.B. a=b.
Dann ist die Gleichung (x²+y²)/a²+z²/c²=1.
Dabei unterscheidet man zwei Fälle, nämlich
c>a oder c<a.
Verlängertes Ellipsoid
...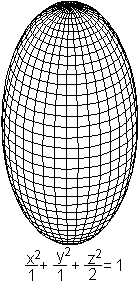 ... ... |
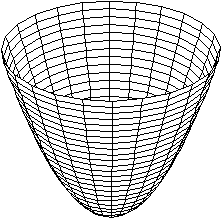
Der Körper links hat die Gleichung (x²+y²)/a²+z²/c²=1,
wobei c>a ist.
Setzt man z=0, so wird die Gleichung zu x²+y²=a².
D.h., eine Hauptellipse wird zum Kreis und mit ihr alle
dazu parallelen Ellipsen. Das Ellipsoid wird dreh- oder rotationssymmetrisch.
Rugbybälle haben z.B. diese Form. |
Man kann den Körper auch so deuten: Eine Kugel wird
in z-Richtung gereckt.
Abgeplattetes
Ellipsoid oder Sphäroid
...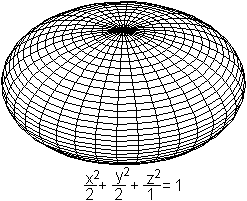 ... ... |
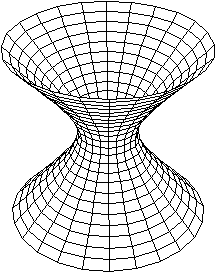
Der Körper links hat die Gleichung (x²+y²)/a²+z²/c²=1,
wobei c<a ist.
Setzt man z=0, so wird die Gleichung zu x²+y²=a².
D.h., eine Hauptellipse wird zum Kreis und mit ihr alle
dazu parallelen Ellipsen.
Das Ellipsoid wird dreh- oder rotationssymmetrisch.
Die Erde ist neben anderen Himmelskörpern in dieser
Weise abgeplattet. Dieses Ellipsoid heißt auch Sphäroid.
Auch Pastillen (z.B. Smarties) haben in etwa diese Form.
|
Man kann den Körper auch so deuten: Eine Kugel wird
in z-Richtung gestaucht.
Man unterscheidet also folgende
Ellipsoide.
Dreiachsiges Ellipsoid
a < b < c
|
Abgeplattetes Ellipsoid
a=b, a<c
|
Verlängertes Ellipsoid
a=b, a>c
|
Kugel
a=b=c
|
Volumen und Oberfläche
top
Das Volumen und die Oberfläche von Rotationsellipsoiden
lassen sich elementar berechnen.
Rotiert eine Kurve mit y=f(x) um
die x-Achse, so gelten für Volumen und Mantelfläche die beiden
folgenden Formeln.
Verlängertes
Ellipsoid
Volumen
...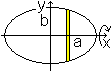 ... ... |
Man stelle sich also vor, die Ellipse mit x²/a²+y²/b²=1
oder y²=(b²/a²)(a²-x²) rotiere um die x-Achse.
Dann gilt
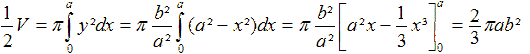
|
Oberfläche
Zur Berechnung des zweiten Integrals stellt man
> die Gleichung x²/a²+y²/b²=1,
> die Ableitung 2x/a²+2(y/b²)y'=0 oder y'=-(2b²x)/(2a²y)
oder y'²=(b4x2)/(a4y2)
und
> den Term sqrt(1+y'²)=sqrt[1+(b4x2)/(a4y2)]=
... = (b/y)sqrt[1- (ex/a²)²] mit e²=a²-b² bereit.
Das führt zu
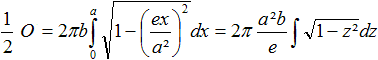
Dabei heißt die Substitution z=ex/a², und
es ist dz=(e/a²)dx oder dx=(a²/e)dz.
Nach Bronstein (4, Seite 47) gibt es zum Integral die
folgende Stammfunktion.
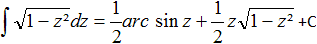
Dann ist
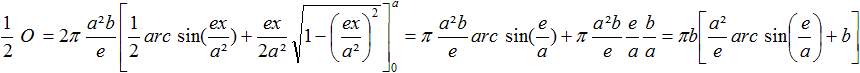
Ergebnis
V=(4/3)pi*ab² und O=2pi*b[b+a²/e*arc sin (e/a)]
mit e²=a²-b²
Abgeplattetes
Ellipsoid oder Sphäroid
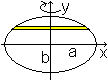
|
V=(4/3)pi*a²b
|
O=2pi*a{a+b²/(2e)*ln[(a+e)/(a-e)]} mit e²=a²-b²
|
Herleitung der beiden Formeln: (1), Seite 443 bis 448 und
Seite 457 bis 462
Dreiachsiges
Ellipsoid
Ellipsoide sind i.a. durch die Halbachsen a, b und c
gegeben. Daraus lassen sich das Volumen und die Oberfläche berechnen.
- Ich belasse es bei der Nennung der Formeln, für die Oberfläche
muss ich mich auf eine Näherung beschränken.
|
V=(4/3)pi*abc
|
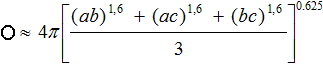
gefunden bei de.wikipedia, mehr steht bei Gérard
P. Michon (URL unten)
|
Flächen
zweiter Ordnung top
Das Ellipsoid gehört zu den Flächen zweiter
Ordnung.
Sie ergeben sich, wenn man in einem räumlichen kartesischen
Koordinatensystem die Gleichung Ax+By+Cz+Dxy+Eyz+Fzx+Gx+Hy+Kz+L=0 graphisch
darstellt.
Bei bestimmten Werten für die Variablen A bis L
ergeben sich im Wesentlichen die folgenden Flächen.
Ellipsoid im Internet
top
Deutsch
Lok Lam Mak (Facharbeit eines Schülers der 12. Klasse)
Das
Volumen eines Hühnereis
PiMath
DIE GESTALT
DER ERDE
Ralf Schaper (Fachbereich Mathematik /Informatik, Universität
Kassel)
Aufgeschnittenes
Ellipsoid
Wikipedia
Ellipsoid,
Rotationsellipsoid
Englisch
F. W. PRESTON
The
Volume of an Egg
Eric W. Weisstein (MathWorld)
Ellipsoid,
Spheroid,
Quadratic
Surface, Superegg
Gérard P. Michon
Spheroids
& Scalene Ellipsoids
Marlene Dieguez Fernandez
Quadric
Surfaces
Richard Parris (Freeware-Programme)
winplot
The Wolfram Demonstrations Project
Ellipsoid,
Eggnigmatica,
EggnigmaticaII,
Lamé's
Ellipsoid And Mohr's Circles
Wikipedia
Ellipsoid,
Spheroid
Xahlee
Ellipsoid,
Rotate
me
Französisch
Robert FERRÉOL (mathcurve)
Ellipsoide
Referenzen top
(1) Georg Ulrich / Paul Hoffmann: Differential- und Integralrechnung
zum Selbstunterricht, Hollfeld [ISBN 3 8044 0575 4]
Mitteilung von Torsten Sillke:
(2) Carlson, B.C., Special Functions of Applied Mathematics,
pp. 261-272, Academic Press, New York (NY), 1977. N.B. In example 9.4-2,
Carlson presents an elegant derivation of the surface area of an ellipsoid
in standard function form.
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |
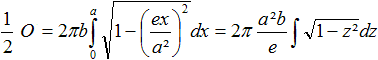






 ...
... ...
...