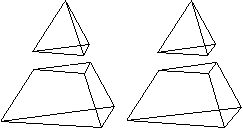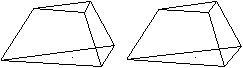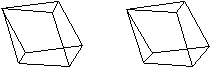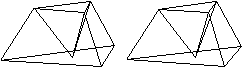Was ist das Tetraeder?
...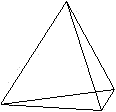 ... ... |
Das Tetraeder ist ein Körper, der von vier gleichseitigen
kongruenten Dreiecken gebildet wird. |
| Das Tetraeder ist ein platonischer Körper. |
 |
Es hat e=4 Eckpunkte, k=6
Kanten und f=4 Seitenflächen. Es gilt die eulersche Polyedersatz e+f=k+2.
Wenn man vom Wort Tetraeder her kommt (Tetraeder heißt
Vierflächner), könnte man jede Dreieckspyramide Tetraeder
nennen. Manchmal wird das Wort auch mit dieser Bedeutung verwendet.
Auf dieser Webseite soll das Tetraeder die oben
beschriebene gerade, regelmäßige Dreieckspyramide sein.
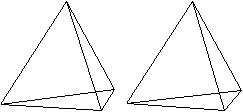
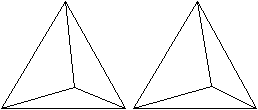
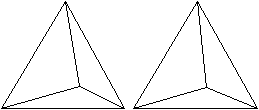
Drei
Ansichten in Stereo
Besondere Ansichten
top
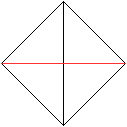
Ein Kante vorne
|
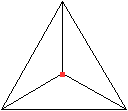
Ein Eckpunkt vorne
|
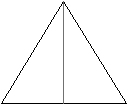
Höhe || Zeichenebene
|
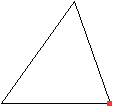
Eine Kante wird zum Punkt.
|
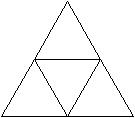
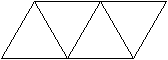
Zwei Netze top
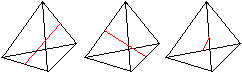
Symmetrien top
>Das Tetraeder ist symmetrisch bezüglich einer Mittelebene.
Es gibt sechs Möglichkeiten.
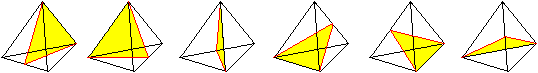
>Es ist drehsymmetrisch mit
der Ordnung 3 mit einer Höhe als Drehachse.
Nach einer Drehung um 120° oder 240° geht das
Tetraeder in sich selbst über.
Es gibt vier Möglichkeiten.
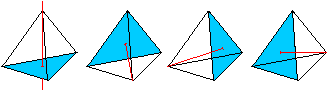
>Es ist drehsymmetrisch mit
der Ordnung 2 mit der Geraden durch die Mittelpunkte zweier windschiefer
Kanten als Drehachse.
Nach einer Drehung um 180° geht das Tetraeder in
sich selbst über.
Es gibt drei Möglichkeiten.
Größen
des Tetraeders top
Das Tetraeder hat die Kantenlänge a, das
Volumen V, die Oberfläche O, den Radius R der
Umkugel, den Radius
r der Inkugel, die Raumhöhe H, den
Abstand zweier windschiefer Kanten
c, den Winkel delta zwischen
einer Kante und Seitenfläche und den Winkel epsilon zwischen
zwei Seitenflächen.
Wenn a die Kantenlänge ist, dann gilt
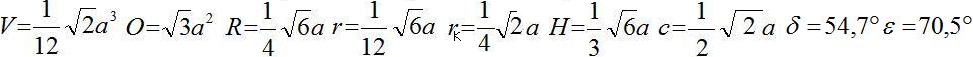
Herleitungen top
Vorweg zwei Formeln des gleichseitigen
Dreiecks mit der Seite a.
Die Höhe ist h = (1/2)sqrt(3)a. Der Flächeninhalt
ist A = (1/4)sqrt(3)a².
Raumhöhe
H
...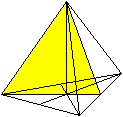 ... ... |
Die Höhe H des Tetraeders erhält man, indem
man zunächst den Mittelpunkt des Grunddreiecks bestimmt. In ihm errichtet
man die Senkrechte, die die Spitze des Tetraeders trifft.
Für die Berechnung betrachtet man das Dreieck aus
zwei Seitenhöhen und einer Kante. |
...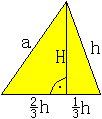 ... ... |
Der Mittelpunkt des Dreiecks ist auch Mittelpunkt der
Seitenhalbierenden. Sie schneiden sich im Verhältnis1:2. Die Abschnitte
sind (1/3)h und (2/3)h. Es gilt h = (1/2)sqrt(3)a.
Nach dem Satz des Pythagoras gilt H² = a²-[(2/3)h]²
= a²-(4/9)h² = a²-(4/9)(3/4)a² = a²-(1/3)a²
= (2/3)a².
Dann ist H=(1/3)sqrt(6)a, wzbw.. |
Radius
der Um- und Inkugel
...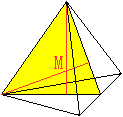 ... ... |
Im Dreieck (a,h,h) liegt eine zweite Raumhöhe.
Der Mittelpunkt M des Tetraeders ist der Schnittpunkt
der eingezeichneten Raumhöhen. |
...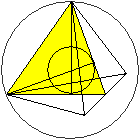 ... ... |
Das Dreieck (a,h,h) liegt in einer Symmetrieebene des
Tetraeders.
In dieser Ebene erscheinen die Um- und Inkugel als Kreise.
Der Mittelpunkt des Tetraeders ist der Mittelpunkt von
In- und Umkugel. |
...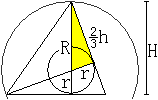 ... ... |
Nach dem Satz des Pythagoras gilt (*) R² = [(2/3)h]²+r².
Weiter ist (**) H = R+r.
Das sind zwei Gleichungen in den Suchvariablen R und r. |
Aus (*) folgt R²-r² = (1/3)a².
Aus (**) folgt R+r = (1/3)sqrt(6)a oder R = (1/3)sqrt(6)a-r.
R wird in die erste Gleichung eingesetzt.
[(1/3)sqrt(6)a-r]²-r² = (1/3)a²
<=> (2/3)a²-(2/3)sqrt(6)ar+r²-r² =
(1/3)a²
<=> (2/3)a²-(2/3)sqrt(6)ar = (1/3)a²
<=> (1/3)a²-(2/3)sqrt(6)ar = 0
<=> (1/2)a = sqrt(6)r
<=> r = (1/12)sqrt(6)a, wzbw.
Weiter ist R = H-r = (1/3)sqrt(6)a-(1/12)sqrt(6)a = (1/4)sqrt(6)a,
wzbw.
Es gilt ferner R:r=3:1.
Volumen
V
Für das Volumen der Pyramide
gilt
V = (1/3)*Adreieck*H
= (1/3)*[(1/4)sqrt(3)a²]*[(1/3)sqrt(6)a] = (1/12)sqrt(2)a³,
wzbw.
Es
gibt eine anschauliche Erklärung des Faktors 1/3.
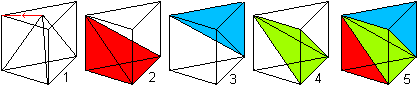 Legt man um das Tetraeder ein Prisma (1) mit dem Volumen
A(Dreieck)*H und verschiebt passend dreimal die Spitze des Tetraeders in
eine Prismaecke (2,3,4), so entstehen drei schiefe Dreieckspyramiden mit
gleichem Volumen. Sie füllen das Prisma aus (5).
Legt man um das Tetraeder ein Prisma (1) mit dem Volumen
A(Dreieck)*H und verschiebt passend dreimal die Spitze des Tetraeders in
eine Prismaecke (2,3,4), so entstehen drei schiefe Dreieckspyramiden mit
gleichem Volumen. Sie füllen das Prisma aus (5).
So ist einzusehen, dass das Volumen eines Tetraeders
gleich (1/3)*Adreieck*H ist.
Oberfläche
O
O=4*[(1/4)sqrt(3)a²]=sqrt(3)a², wzbw.
Abstand
zweier windschiefer Kanten c
...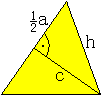 ... ... |
Der Abstand zweier windschiefer Kanten kommt im Dreieck
(a,h,h) in wahrer Länge vor.
Nach dem Satz des Pythagoras ist c² = h²-[(1/2)a]²
= [(1/2)sqrt(3)a]²-(1/4)a² = (1/2)a².
Dann ist c = (1/2)sqrt(2)a, wzbw.. |
Der halbe Abstand ist der
Radius der Kantenkugel, der Kugel durch die Kantenmitten,rk = (1/4)sqert(2)a.
Winkel im Tetraeder
...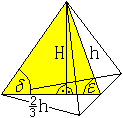 ... ... |
Für den Winkel zwischen einer Kante und einer Seitenfläche
gilt tan(delta)=H/[(2/3)h]=sqrt(2).
Das führt zu einem Winkel von delta = 54,7° (gerundet).
|
Für den Winkel zwischen
zwei Seitenflächen gilt
sin(epsilon) = H/h = [(1/3)sqrt(6)a]/[(1/2)sqrt(3)a]
= (2/3)sqrt(2).
Das führt zu einem Winkel von epsilon = 70,5°
(gerundet).
Tetraeder im Würfel
top
... |
...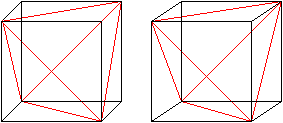 ... ... |
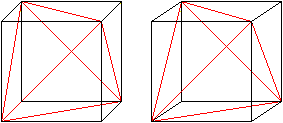
Zeichnet man in einen Würfel
6 passende Flächendiagonalen ein, so entsteht ein Tetraeder.
Es gibt zwei Möglichkeiten. |
Oktaederstern
...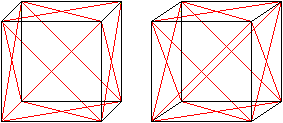 ... ... |
Zeichnet man alle Flächendiagonalen, so entsteht
ein Stern mit 8 Zacken. |
...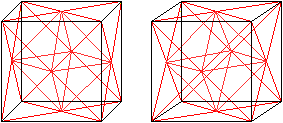 ... ...
|
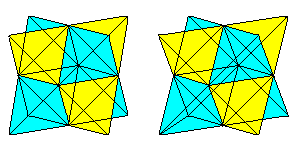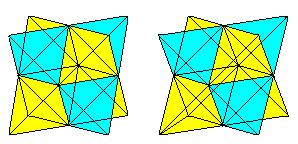 ... ...
|
Man erkennt den Stern besser, wenn man auch die nebeneinander
liegenden Flächenmitten des Würfels miteinander verbindet. |
Der Stern kann auch als Oktaeder
angesehen werde, auf dessen Seitenflächen 8 Tetraeder liegen.
Liegt das Tetraeder im Würfel,
so hat es in einem kartesischen Koordinatensystem folgende Darstellung.
...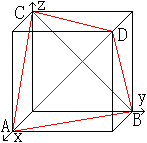 ... ... |
Der Würfel habe die Kantenlänge e. Dann gilt
für die Tetraederkante a=sqrt(2)e.
Die Koordinatendarstellung ist:
A(e|0|0)
B(0|e|0)
C(0|0|e)
D(e|e|e)
|
Tetraeder
im Pentagondodekaeder top
... ... ...
|
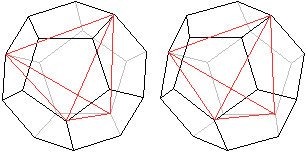
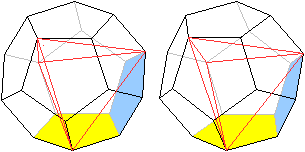
Zeichnet man in ein Pentagondodekaeder
6 passende Diagonalen, so entsteht ein Tetraeder. |
Das Tetraeder findet man
in mehreren Schritten.
... ... ...
|
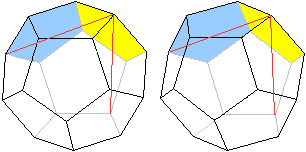
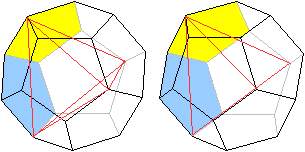
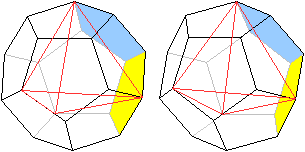
>Färbe 2 nebeneinander liegende Fünfecke.
>Zeichne eine Kantenlänge des Tetraeders, indem
du vom linken Punkt des Fünfecks aus auf der Umrisslinie 3 Kantenlängen
im Uhrzeigersinn weiter gehst.
>Gehe dann im gelben Fünfeck vom Endpunkt aus 2
Kanten entlang des gelben Fünfecks weiter und dann von ihm weg eine
Kante weiter. |
... ... ...
|
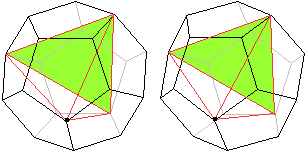
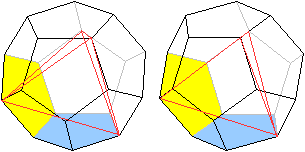
>Zeichne das grüne Dreieck.
>Suche den Eckpunkt, der über dem Dreieck liegt.
Er ist in der Zeichnung als ein kleines, schwarzes Quadrat
markiert.
Das ist der vierte Eckpunkt des Tetraeders, der noch
mit den 3 anderen zu verbinden ist. |
Es gibt noch 4 weitere Tetraeder,
die man über die farbigen Fünfecke findet.
Sternkörper aus 5 Tetraedern
...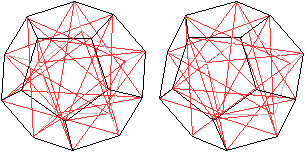 ... ... |
Legt man die 5 Tetraeder im Pentagondodekaeder übereinander,
so ergibt sich ein Sternkörper.
Obwohl man im nebenstehenden Stereo-Bildpaar die Tetraeder
nicht mehr trennen kann, lässt sich gut erkennen, dass die 5 Tetraeder
je einen der 20 Eckpunkte des Dodekaeders besetzen, 20=4*5. |
Auf der Webseite von Gerd Müller (URL unten) findet
man bessere Bildpaare. Dort kann man auch nachlesen, dass auch das Ikosaeder
5 Tetraeder enthält. Die Eckpunkte liegen in den Mittelpunkten der
Seitenflächen. Das Ikosaeder ist nämlich der duale Körper
des Dodekaeders.
Ein farbiges Bild mit den Schnittlinien der Tetraeder
findet man bei Wikipedia unter dem Namen
Compound of five tetrahedra.png
(URL
unten).
Tetrapode top
... ... ... |
... ... ... |
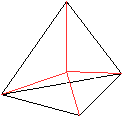
Verbindet man den Mittelpunkt des Tetraeders mit seinen
Eckpunkten, so entsteht ein räumliches Gebilde aus vier Radien der
Umkugel.
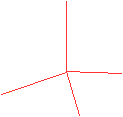
Baut man nach diesem Vorbild ein Gerät aus vier
Stäben und wirft es hin, so steht ein Stab immer vertikal. |
>Es heißt Krähenfuß (englisch Caltrop),
wenn man es als Waffe verwendet. Es ist dann z.B. eine Eisenkugel mit vier
scharfen Spitzen, die Fahrzeuge mit Reifen nicht überwinden können.
>Es heißt Tetrapode, wenn man es aus Beton, viele
Tonnen schwer, herstellt. Man verwendet ihn für Seebefestigungen.
Die Tetrapoden verhaken sich.
...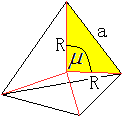 ... ... |
Man erhält den Winkel my zwischen den Stäben
mit Hilfe des Kosinussatzes.
Es gilt a²=R²+R²-2R²cos(my) mit R=(1/4)sqrt(6)a
oder R²=(3/8)a².
Dann ist a²=(3/4)a²-(3/4)a²cos(my) oder
(1/4)=-(3/4)cos(my).
Daraus folgt cos(my)=-1/3 oder my=109,5°. |

|
Tetrapoden, entdeckt vor Rethymnon/Kreta 11/2003 |
Tetraederzahlen top
...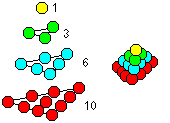 ... ... |
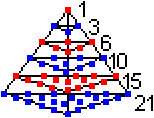
Man kann Kugeln zu immer größer werdenden
Tetraedern aufschichten. Die Anzahl der Kugeln in einer Schicht ist 1,3,6,10,...
, allgemein n(n+1)/2.
Bildet man die Summe der Kugeln eines Tetraeders, so
erhält man die Tetraederzahlen
1,4,10,20,... , allgemein 1+3+6+10+...+n(n+1)/2 = n(n+1)(n+2)/6. |
...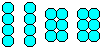 ... ... |
Klebt man 20 Kugeln zu zwei Vierergruppen und zwei
Sechsergruppen zusammen, so erhält man ein bekanntes Puzzle: Man soll
die vier Stücke zu einem Tetraeder zusammensetzen. |
Es gibt viele Puzzles dieser Art. Einige findet man beschrieben
auf meiner Webseite Tetraederpuzzles.
Der
Tetraeder von Bottrop top
Im Ruhrgebiet gibt es an der A 42 seit 1996 ein Ausflugsziel:
Ein Stahlgebilde in Tetraederform. Es ist der
Tetraeder von Bottrop, entworfen vom Architekten Prof. Wolfgang Christ.
Der Tetraeder hat eine Kantenlänge von 60 m.
... ... ... |
Er befindet sich weithin sichtbar auf einer Abraumhalde
aus den Zeiten des Kohleabbaus, der Halde Beckstraße in Bottrop.
Die nebenstehende Aufnahme entstand am 7.8.2010. Ausgerechnet
an diesem Tage wurde uns aus Sicherheitsgründen - unten stehen Bierbuden
- ein Aufstieg verwehrt. |
Mit dem 3D-Blick erkennt
man den Aufbau.
...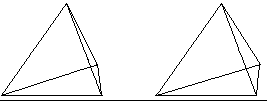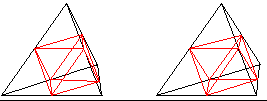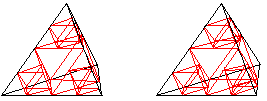 ...... ...... |
In ein Tetraeder wird ein Oktaeder gelegt, indem man
alle sechs Kantenmitten miteinander verbindet. Dabei entstehen in den Ecken
vier halb so große Tetraeder. In drei dieser halb so großen
Tetraeder wiederholt sich die Struktur: In ihnen liegen wiederum Oktaeder.
Ein Tetraeder (unten, hinten) bleibt leer. |
...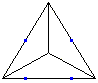 ... ...
|
Der Stahlkoloss ruht auf vier 9 m hohen Säulen (dunkelblau),
die ein Rechteck bilden. Man erkennt die Lage am besten in der Aufsicht. |
...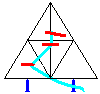 ... ...
|
Zum Besteigen sind innen im Kontrast zum strengen Äußeren
drei Aussichts-Plattformen (rot) und Treppen eingehängt.
Man gelangt zu der unteren Plattform über eine leicht
geneigte Treppe. Die Treppe zur mittleren, ringförmigen Plattform
ist etwas steiler. Zur höchsten Plattform gelangt man über eine
Spindeltreppe. Die oberste Plattform liegt etwas schräg und ist auch
ringförmig. |
Raumausfüllung top
Es gibt in der Mathematik das Problem der vollständigen
Raumausfüllung durch Körper. Jeder sieht ein, dass Packungen
von Würfeln den Raum ausfüllen. Das gelingt aber nicht mit Tetraedern.
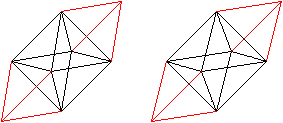
Erst wenn man eine Kombination von Oktaedern und Tetraedern,
wie sie beim Tetraeder von Bottrop vorkommen, vorgibt, klappt das. Ein
Oktaeder (schwarz) und zwei Tetraeder (rot) bilden ein Parallel-Epiped.
Das ist ein gereckter Würfel. So wie die Würfel füllen auch
die verbogenen Würfel, die Parallelepipede, den Raum aus.
Vom
Tetraeder zu anderen Körpern top
Oktaeder
...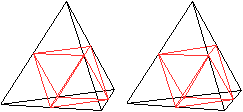 ... ... |
Verbindet man die Mittelpunkte der Kanten eines Tetraeders,
so entsteht ein Oktaeder. |
Tetraeder
...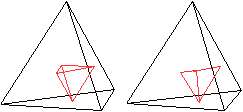 ... ... |
Verbindet man die Mittelpunkte der Seitenflächen
eines Tetraeders, so entsteht ein kleineres Tetraeder.
Das bedeutet, dass das Tetraeder selbstdual ist. |
Triangulare
Bipyramide
...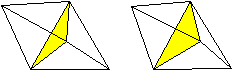 ... ... |
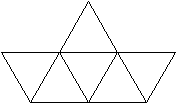 ... ... |
Spiegelt man das Tetraeder an einer Seitenfläche,
so entsteht eine Bipyramide.
Dieser Körper aus sechs gleichseitigen Dreiecken
gehört zu den acht konvexen Deltaedern
und auch zu den 92 Johnson-Körpern (J12). |
Tetraederstumpf
Der Tetraederstumpf entsteht aus einem Tetraeder, indem
man an den Ecken dreiseitige Pyramiden abschneidet. Dazu teilt man die
Kanten in drei gleiche Teile.
...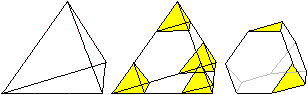 ... ...
|
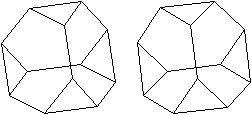
|
Mehr auf meiner Webseite Tetraederstumpf
Triakistetraeder
...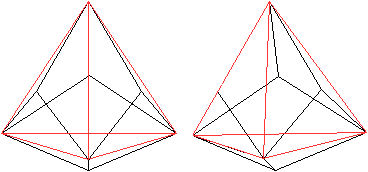 ... ... |
Das Triakis-Tetraeder ist ein Tetraeder, auf dessen Seitenflächen
vier passende Dreieckspyramiden gesetzt werden. |
Mehr auf meiner Webseite Triakistetraeder
Teilstück
eines Prismas
...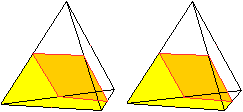 ... ... |
Verbindet man vier passende Mittelpunkte von Kanten,
so entsteht ein Quadrat. Legt man eine Schnittebene durch das Quadrat,
so wird das Tetraeder in zwei kongruente Abschnitte von Dreiecksprismen
aufgeteilt. |
... ... ... |
Werden sie aus Holz gefertigt, so hat man ein Puzzle
mit Aha-Effekt:
Baue aus den beiden Stücken ein Tetraeder! |
Cayleysche
Fläche
...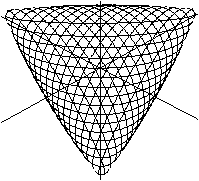 ... ... |
Die cayleysche Fläche ist
eine kubische geschlossene Fläche mit x²+y²+z²=2xyz+1.
Zum Vergleich: Die Einheitskugel hat die Darstellung x²+y²+z²=1.
Der innere Bereich hat die Form eines "abgerundeten" Tetraeders. |
Sierpinski-Tetraeder
... ... ... |
Entfernt man aus einem Tetraeder ein Oktaeder, so entsteht
ein Restkörper aus vier Tetraedern. Das ist das einfachste Sierpinski-Tetraeder.
Entfernt man aus diesen Tetraedern sukzessiv Oktaeder,
so entsteht eine Folge von Restkörpern, die Sierpinski-Tetraeder. |
Es
sei n die Nummer des Sierpinski-Tetraeders, N die Anzahl der Tetraeder,
L die Länge eines Tetraeders und V das Volumen des n-ten Tetraeders.
Dann lassen sich zu den Sierpinski-Tetraedern
folgende Angaben machen.
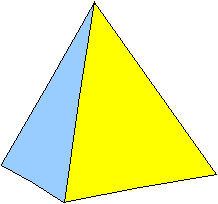
n=0, N=1, L=1, V=1
|
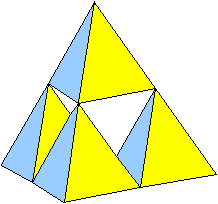
n=2, N=4, L=1/2, V=1/2
|
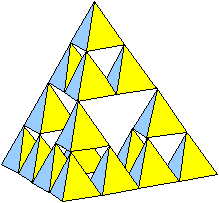
n=2, N=16, L=1/4, V=1/4
|
Allgemein gilt
L=2-n
N=4n
V=2-n |
Für n gegen Unendlich gehen das Volumen und die
Oberfläche gegen Null.
Tetraederstumpf
Die Größe V ist das Volumen des Tetraeders.
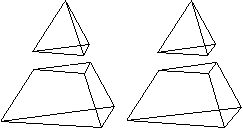
Schnitt auf halber Höhe
V=(7/8)V+(1/8)V
|
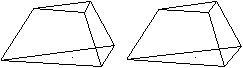
Tetraederstumpf
Vstumpf=(7/8)V
|
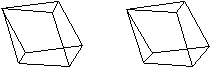
Stumpf ohne Ecke
Vstumpf2=(3/4)V
|
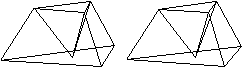
Stumpf mit Vertiefung
Vstumpf3=(3/4)V
|
Basteleien top

Papier und Kleber
|

Zahnstocher und Bostik
|

Kugeln und Stabmagnete
|

Auf folgenden Seiten meiner Homepage geht es auch um
Tetraeder.
Tetraeder im Internet
top
Deutsch
Christof Weber
Was
hat dieser Körper mit Kugeln zu tun? (Reuleaux'sche Tetraeder)
FAZ
Tetraederpackung:
Eins geht noch
Gerd Müller
Platonische
Körper in Stereodarstellung
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder
Michael Holzapfel
Tetraedergruppe
und symmetrische Gruppe S4
Rainer Deissler (Pädagogische Hochschule Freiburg)
Sierpinski-Tetraeder
bauen
Wikipedia
Tetraeder,
Sterntetraeder,
Tetraeder
(Bottrop),
Tetrapode,
Tetraederzahl,
Krähenfuß,
Reuleaux-Tetraeder,
A4
(Gruppe)
Englisch
Eric W. Weisstein (World of Mathematics)
Tetrahedron,
Isosceles
Tetrahedron, Stella
Octangula, Tetrahedron2-Compound,
Tetrahedron4-Compound,
Tetrahedron5-Compound,
Meissner
Tetrahedron
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetrahedron
Wikipedia
Tetrahedron,
Stellated
octahedron, Tetrahedral
symmetry, Tetrapod
(structure), Tetrahedral
number, Tetrahedral
kite,
Reuleaux
tetrahedron, Compound
of five tetrahedra.png
Französisch
TETRAÈDRE,
TRIAKI-TÉTRAÈDRE,
SURFACE
DE CAYLEY
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist in der Version von 2001 auch in Englisch
vorhanden.
URL meiner
Homepage: https://www.mathematische-basteleien.de/
©
2001, überarbeitet 2012, Jürgen Köller
top |
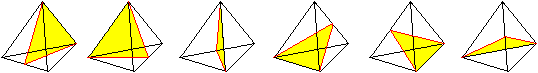


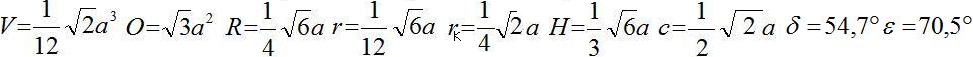



 ...
...




 ...
... ...
... ...
... ...
...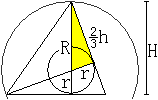 ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
...
 ...
...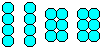 ...
... ...
... ......
...... ...
... ...
... ...
... ...
...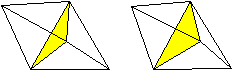 ...
... ...
...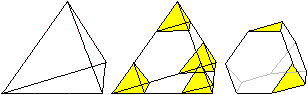 ...
...

 ...
... ...
... ...
...