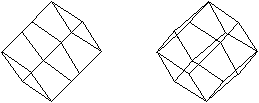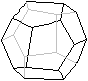
Rhombendodekaeder

Inhalt dieser Seite

Was ist ein Rhombendodekaeder?
Beschreibung
Entstehung
Größen
Raumausfüllung

Der duale Körper
Stern-Puzzle
Hyperwürfel
Rhombendodekaeder im Internet
.

Zur Hauptseite "Mathematische Basteleien"

Was ist ein Rhombendodekaeder?

Ein Rhombendodekaeder ist ein Körper, der von 12 kongruenten Rauten gebildet wird.
Der Name ergibt sich aus der anderen Bezeichnung für die Raute, dem Rhombus, und Dodekaeder heißt Zwölfflächner.

Es gibt weitere Dodekaeder.

...

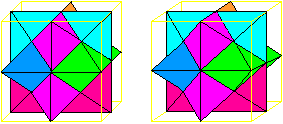
Bekannt ist das Pentagondodekaeder.

Die Bildpaare auf dieser Seite ermöglichen dreidimensionale Ansichten.

Beschreibung
Ecken, Kanten, Flächen top
Das Rhombendodekaeder hat neben den 12 Seitenflächen 14 Ecken und 24 Kanten.
In acht Eckpunkten treffen drei Kanten und damit auch drei Rauten zusammen.
In sechs Eckpunkten treffen vier Kanten und damit auch vier Rauten zusammen.

1.Ring aus Rauten top
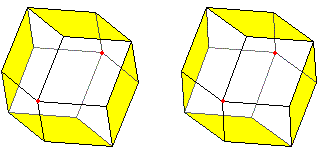
Vier Rauten hintereinandergehängt bilden einen Ring. Sie trennen zwei Spitzen (rot) gebildet aus je vier Rauten.

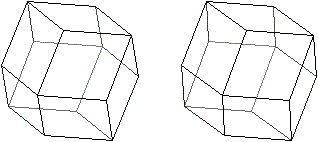
Man kann die Zeichnung auch so interpretieren:
Zwei parallele Rauten sind Deck- und Grundfläche. Dazwischen liegen zehn Rauten. Zwei stehen aufrecht und trennen zwei Spitzen, gebildet aus je vier Rauten.

2.Ring aus Rauten top
Sechs Rauten bilden einen Zickzack-Ring. Sie trennen zwei Spitzen (rot) gebildet aus je drei Rauten.

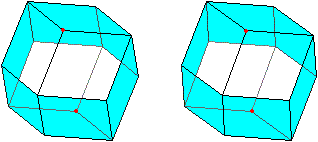
Besondere Ansichten top

...

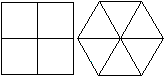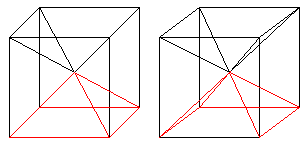
Schaut man senkrecht auf die Ecken des Dodekaeders, ergeben sich einfache Figuren.
Ein Blick auf einen Eckpunkt mit vier Kanten führt zu einem Quadrat mit zwei Mittelparallelen. Laufen an einem Eckpunkt drei Kanten zusammen, ergibt sich ein Sechseck mit Diagonalen.
Es handelt sich hier um zwei senkrechte Parallelprojektionen.

Netz top

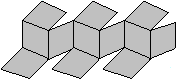
Vier Parallelepipede im Dodekaeder top
Zeichnet man in ein Dodekaeder alle Raumdiagonlalen, so erkennt man im Inneren vier Parallelepipede, aus denen sich das Dodekaeder zusammensetzt.

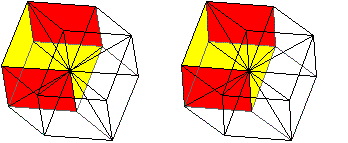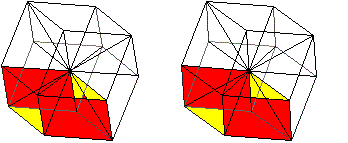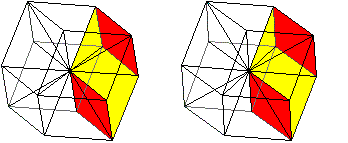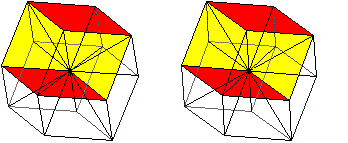
Acht Dreieckspyramiden top
Zeichnet man in Rot alle langen Diagonalen der Rauten, so entstehen acht Dreieckspyramiden.

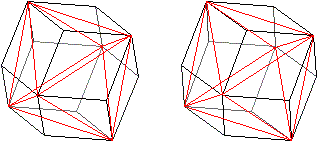
Im Inneren des Dodekaeders liegt ein Oktaeder.

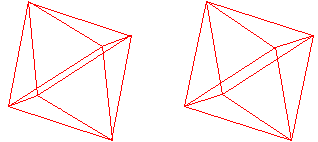
Vier der aufgesetzten Dreieckspyramiden bilden ein Tetraeder.

Sechs Viereckspyramiden top
Zeichnet man in Rot alle kurzen Diagonalen der Rauten, so entstehen sechs quadratische Pyramiden.

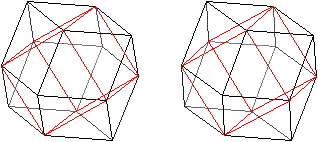
Im Inneren des Dodekaeders liegt ein Würfel:

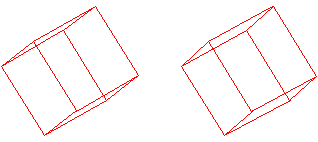
Entstehung top
Das Dodekaeder besteht also aus einem Würfel mit sechs quadratischen Pyramiden auf den Seitenflächen.
Die Pyramiden werden durch die Raumdiagonalen eines gleich großen Würfels erzeugt.

Das folgende "Animated Gif" demonstriert noch einmal die Entstehung einer Raute.

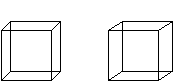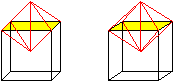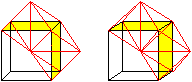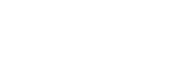
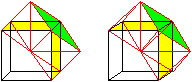
Die Seitenflächen zweier verschiedener Pyramiden liegen paarweise in einer Ebene und bilden eine Raute. Deshalb kann man z.B. im ersten Bild auf dieser Seite den Zentralwürfel und die aufgesetzten Pyramiden nicht erkennen.

Das Rhombendodekaeder ist im Aufbau also gar nicht so kompliziert. Damit verliert es etwas von seiner Faszination.

Pyramidenwürfel

...

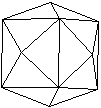Es gibt auch allgemeiner den "Pyramidenwürfel" oder Tetrakishexaeder.

Auch da werden auf die Würfelflächen Pyramiden gesetzt. Meist sind sie flacher.
Flußspat kann in dieser Form kristallisieren.

Größen top
Die Raute als Seitenfläche hat die Seitenlänge s, die Diagonalen d und e und die Innenwinkel alpha und 180°-alpha.
Das Dodekaeder hat das Volumen V und die Oberfläche O.

Gegeben sei die Kantenlänge a des erzeugenden Würfels.
Die übrigen Größen ergeben sich aus der quadratischen Pyramide, die auf einen Würfel gesetzt wird.

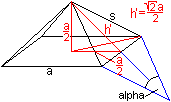...... Zuerst zur Raute:
Die Kantenlänge a ist gleichzeitig die kürzere Diagonale, d=a.
Die andere Diagonale ist e=2h'=sqrt(2)a. Die Diagonalen stehen im Verhältnis 1:sqrt(2).
Die Seitenlänge der Raute ist halb so groß wie die Raumdiagonale des Würfels, s=sqrt(3)a/2.
Die Fläche ist sqrt(2)a²/2. Der kleinere Winkel ist alpha=2*arc tan (sqrt(2)/2)=70,5°.

Die Oberfläche des Dodekaeders besteht aus 12 Rauten: O=12sqrt(2)/2*a²=6sqrt(2)a².
Das Volumen ist 2a³.

Ist die Seite s des Dodekaeders bekannt, ergeben sich O=8sqrt(2)s² und V=(16/9)sqrt(3)s³.

Raumausfüllung top
Es ist bekannt, dass der Würfel den dreidimensionalen Raum ausfüllt ("parkettiert").
Das schafft auch das Rhombendodekaeder:

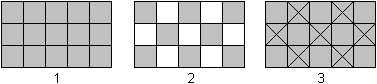1 Das sei eine Darstellung des Raums, der von Würfeln ausgefüllt wird, im Querschnitt (und als Ausschnitt).
2 Man stelle sich vor, dass jeder Würfel isoliert wird und seine sechs Nachbarwürfel verliert.
3 Diese sechs Hohlräume in der Umgebung eines jeden Würfels mögen durch quadratische Pyramiden ersetzt werden, die aus einem Würfel durch die Raumdiagonalen erzeugt werden. Jeder Würfel mit den sechs aufgesetzten Pyramiden aber ist ein Rhombendodekaeder.
Ergebnis: Die Rhombendodekaeder füllen den Raum aus.

Der duale Körper top
Verbindet man die Mittelpunkte der 12 Rauten, so entsteht ein Kuboktaeder.

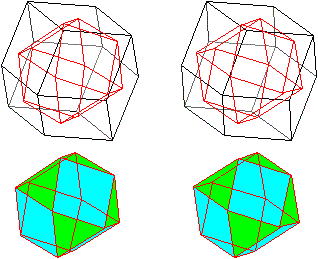
Verbände man die Mittelpunkte der Seitenflächen des Kuboktaeders, so entstünde umgekehrt ein Rhombendodekaeder. Rhombendodekaeder und Kuboktaeder sind duale Körper.

Mehr über das Kuboktaeder findet man an anderer Stelle meiner Homepage.

Stern-Puzzle top
Das klassische Stern-Puzzle ist ein "stellated rhombic dodecahedron". Damit wird ausgedrückt, dass zur Erzeugung des Sterns ein Rhombendodekaeder mit Zacken in Pyramidenform versehen wird. Die Spitzen der Zacken liegen dabei in Kantenmitten eines umhüllenden Würfels.

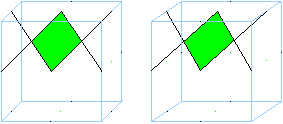
Eine Raute entsteht, indem man passende Flächen- und Kantenmitten des erzeugenden Würfels verbindet.

Sucht man auf diese Weise die übrigen Rauten, entsteht das folgende Bild eines Rhombendodekaeders.

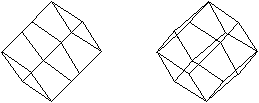
Mehr findet man auf meiner Seite Stern-Puzzle.

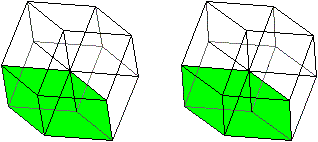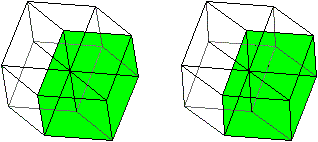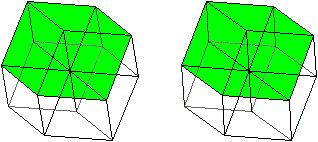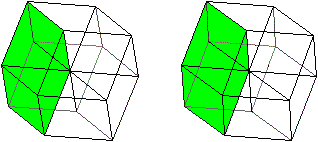
Hyperwürfel top
Verbindet man die gegenüberliegenden Eckpunkte des Dodekaeders, bei denen nur drei Kanten zusammentreffen, so gehen von jeder Ecke vier Strecken aus. Diese Raumdiagonalen treffen sich in einem Punkt.
In dieser Form kann das Dodekaeder auch als Modell des Hyperwürfels angesehen werden.

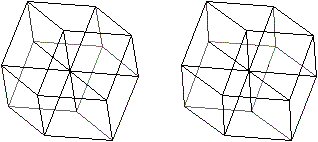
Ein Hyperwürfel wird von acht Würfeln gebildet.

Mehr über den Hyperwürfel findet man an anderer Stelle meiner Homepage.

Referenzen top
(1) Hugo Steinhaus: 100 Aufgaben, Leipzig-Jena-Berlin, 1968
(2) Jan Gullberg: Mathematics - From the Birth of Numbers, New York - London 1997 (ISBN0-393-04002-X)
(3) Heinrich Hemme: Das Rhombendodekaeder: ein Körper, der es in sich hat, bild der wissenschaft 10-1986
(4) Heinrich Hemme: Die Mathematik der Bienenwaben, bild der wissenschaft 06-1994

Rhombendodekaeder im Internet top

Deutsch

Anton Ernst Lafenthaler
Das kubische Kristallsystem

Heinrich Hemme (Aus Spektrum der Wissenschaft Juni 1994, Seite 12ff.)
Die Mathematik der Bienenwaben

H.B.Meyer
Rhombendodekaeder aus (vier) Flechtstreifen

Horst Steibl
Rautendodekaeder (.ppt-Datei)