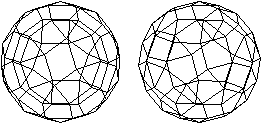|
Was ist ein Quadrat?
 .
|
Ein Quadrat ist ein Viereck mit vier rechten Winkeln
und vier gleichen Seiten. |
... .... |
Die gleiche Figur steht auf der Spitze.
Man nennt sie ein Karo, auch wenn man weiß, dass
es ein Quadrat ist.
Man will mit diesem Wort die Lage des Quadrates ausdrücken. |
Größen
des Quadrats
top
... ... |
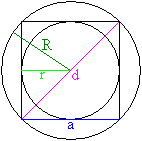Das Quadrat hat 4 gleiche Seiten.
2 Seiten treffen sich in einer
Ecke und stehen aufeinander senkrecht.
Die Länge einer Seite sei
a.
Das Quadrat hat 2 Diagonalen der
Länge d=a*sqr(2).
Der Flächeninhalt beträgt
A=a², der Umfang 4a.
Der Umkreis hat den Radius R=a*sqr(2)/2, der Inkreis
den Radius r=a/2. |
Eine Formel zum
Quadrat top
... ...
|
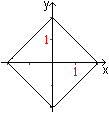
Es ist möglich, ein Quadrat in einem Koordinatensystem
nur durch
eine Gleichung zu beschreiben.
|x|+|y|=2 oder abs(x)+abs(y)=2
|
Quadratzahlen top
Man erhält die Quadratzahlen, wenn man die natürlichen
Zahlen mit sich selbst multipliziert.
... ... |
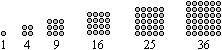Die Quadratzahlen lassen sich durch Quadrate aus gleichen
Figuren darstellen. |
|
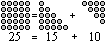
Jede Quadratzahl ist gleich der Summe zweier Dreieckszahlen.
Formel: n²=[1+2+3+...+n] + [1+2+3+...+(n-1)] |
 |
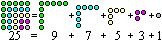Jede Quadratzahl n² ist gleich der Summe der n ersten
ungeraden Zahlen.
Formel: n²=1+3+5+...+(2*n-1) |
|
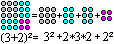
Ein Quadrat kann in zwei kleinere Quadrate und zwei gleiche
Rechtecke zerlegt werden.
Es gilt nämlich die erste binomische Formel (a+b)²=a²+2*a*b+b². |
... ...
|
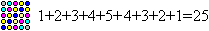Ein Quadrat kann man in Streifen in Diagonalrichtung
zerlegen.
Es gilt 1+2+3+...+n+...3+2+1=n².
 |
Mehr findet man auf meiner
Seite Quadratzahlen.
Halbieren eines
Quadrats top
Es gibt viele Möglichkeiten
die Fläche eines Quadrates zu halbieren. Hier sind fünf.
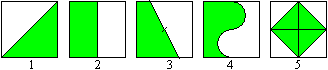Zu 1 und 2: Normalerweise wird ein Quadrat durch eine Diagonale
oder Mittellinie halbiert. So kann ein quadratisches Stück Papier
gefaltet werden.
Zu 3: Jede Gerade durch den Mittelpunkt des Quadrates
teilt es in zwei kongruente Trapeze.
Zu 4: An Stelle der Geraden kann man auch andere Linien,
z.B. zwei Halbkreise, nehmen.
Zu 5: Die Figur in der Mitte besteht aus vier kongruenten
Dreiecken, das ganze Quadrat aus acht. Also ist die Halbierung gesichert.
Hat das Ausgangsquadrat die Länge 2, so hat das grüne Quadrat
die Länge sqr(2). Die Bedeutung dieser Figur liegt darin, dass das
äußere Quadrat eine rationale, das innere eine irrationale Seitenlänge
hat.
Quadrate im Quadrat
top
Das Quadrat durch Teilpunkte
... .... |
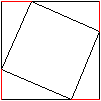Trägt man eine Strecke (rot) von jeder Ecke aus
immer in die gleiche Richtung ab, so entstehen vier Punkte. Verbindet man
diese vier Punkte, so entsteht ein Viereck.
Behauptung: Das Viereck ist ein Quadrat.
Beweis: Die vier Dreiecke sind nach SWS kongruent.
W kennzeichnet den rechten Winkel. Folglich sind die Hypotenusen gleich
und das sind gerade die Quadratseiten. Eine einfache Winkelbetrachtung
führt zu rechten Winkeln des Vierecks. |
Ein Quadrat im Inneren
... ... |
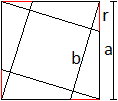Verbindet man die vier Teilpunkte jeweils mit einem Eckpunkt,
so entsteht im Inneren ein Quadrat.
Sind die Seite des Quadrats mit a und das Teilverhältnis
mit r:(a-r) gegeben, so ist die Seitenlänge b des inneren Quadrates
b = (a²-ar)/sqrt(a²+r²).
|
Herleitung
Es werden die Hilfsvariablen x, y und z eingeführt.
 |
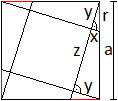Es gilt nach dem Satz des Pythagors r² = x²+y².
Es gilt nach dem 2. Strahlensatz y:x = a:r. Daraus folgt
y = (ax)/r.
Das sind zwei Gleichungen mit den Variablen x und y.
Sie haben die Lösung x = r²/sqrt(a²+r²)
und y = (ar)/sqrt(a²+r²).
Für die Verbindungslinie eines Teilpunktes mit dem
Eckpunkt gilt z² = a²+r². Dann ist z = sqrt(a²+r²). |
Die Seitenlänge des
inneren Quadrates ist
b = z-x-y = sqrt(a²+r²)-r²/sqrt(a²+r²)-(ar)/sqrt(a²+r²)
= (a²+r²-r²-ar)/sqrt(a²+r²) = (a²-ar)/sqrt(a²+r²),
wzbw.
Quadrat und Kreis
top
 |
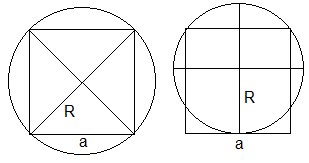In der rechten Zeichnung geht ein Kreis durch alle vier
Ecken eines Quadrats.
Das ist der Umkreis mit R=(1/2)sqrt(2)a oder ungefähr
0,7a.
In der linken Zeichnunggeht ein Kreis durch zwei Ecken
und berührt eine Seite.
Nach dem Höhensatz ist der Radius R=(5/8)a oder
ungefähr 0,6a.
|
Eine Folge von
Quadraten top
.. .... |
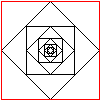Das rote Quadrat habe die Seitenlänge a und es hat
somit den Flächeninhalt a².
Für die Summe der Flächeninhalte der inneren
Quadrate ergibt sich
A= a²/2 + a²/4+a²/8+a²/16+... = a²(1/2+1/4+1/8+1/16+...).
In der Klammer steht eine geometrische Reihe mit dem
Grenzwert 1. |
Ergebnis: Die Summe der Flächeninhalte der inneren
Quadrate strebt gegen den Flächeninhalt des großen Quadrates.
Auch die binomischen Formeln und
der Satz des Pythagoras behandeln Quadrate.
Ich verweise dazu auf meine Webseite Formeln
im Bild.
Parkettierungen
mit Quadraten
top
Es ist leicht, ein Quadrat in gleiche Quadrate aufzuteilen.
Es ist aber schwer, verschiedene Quadrate zu finden,
die das leisten.
... ... |
Man braucht mindestens 21 Quadrate, die ein Quadrat bilden
(Duijvestijn 1962, 1978).
Lösung
112² = 50²+42²+37²+35²+33²+29²+27²+25²+24²+19²+18²+17²+16²+15²+11²+9²+8²+7²+6²+4²+2² |
Mit diesem Problem haben sich viele Mathematiker (und Computer)
beschäftigt (Buch 2). Mehr findet man aud Erich Friedmans web site
(URL unten).
Eine geometrische
Reihe top
... ... |
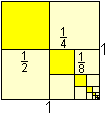Die geometrische Reihe 1/4+1/16+1/64+... hat den Grenzwert
1/3.
Nachweis: s=a0[1/(1-q)]=(1/4)[1/(1-(1/4)]=1/3
Links ist eine bemerkenswerte Veranschaulichung.
Entdeckt bei http://en.wikipedia.org/wiki/The_Quadrature_of_the_Parabola |
Größte
und kleinste Rechtecke top
Das Quadrat ist ein Grenz-Rechteck. Das drückt sich
in den Lösungen der folgenden Extremwertaufgaben aus.
Aufgabe 1) Welches der Rechtecke mit gleichem Umfang
hat den größten Flächeninhalt?
Aufgabe 2) Welches der Rechtecke mit gleichem Flächeninhalt
hat den kleinsten Umfang?
Aufgabe 3) Welches Rechteck im gleichseitigen Dreieck
hat den größten Flächeninhalt?
Aufgabe 4) Welches Rechteck im Quadrat hat den größten
Flächeninhalt?
Aufgabe 5) Welches Rechteck im Kreis hat den größten
Flächeninhalt?
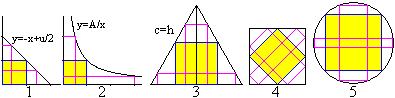In allen Fällen ist ein Quadrat das gesuchte Rechteck.
Das größte Quadrat im Würfel findet man
in meiner Würfelseite.
Darstellung
von Ziffern durch Quadrate top
Matrix aus Quadraten für Zeichen
Die Pixel zur Darstellung der Zeichen eines Schriftsatzes
bilden eine Matrix kleiner Quadrate, die erst bei hinreichender Vergrößerung
sichtbar werden.
... ...
|
Beispielsweise verwendet man für das Bild der Zahl
2
eine Rechteck mit 9x14 Pixels im Schriftsatz "Times New Roman" von Winword. |
.. ....
|
... ...
|
Verdoppelt man ein Quadrat, so erhält man die Figur
links, mit der die zehn Ziffern gut dargestellt werden können (rechts).
Diese Anzeige kennt man vom Taschenrechner. |
.. ....
|
Ring des Salomon
.. ....
|
Nach einer alten Legende erzählt Lucas, dass auf
einem Ring Salomos ein Quadrat mit den Diagonalen eingraviert war (links).
In diesem Zeichen stecken die zehn Ziffern (rechts) [Buch
1]. |
.. ....
|
Tastatur eines Taschenrechners
In diesem Zusammenhang kann man auch die Tastatur eines
Taschenrechners anführen. Die Ziffern 1 bis 9 stehen auf quadratischen
Tasten. Sie bilden ein 3x3-Quadrat. Merkwürdigerweise laufen die Zahlen
von unten links nach oben rechts. Die Tastatur des Tastentelefons oder
des Handys laufen von links oben nach rechts unten wie unsere Schrift.
Ich kann mich erinnern, dass man versuchte, eine einheitliche
Tastatur zu schaffen, zumal die Tastentelefone zuerst da waren. Das misslang.
Die ersten erschwinglichen Rechner kamen aus Fernost, die Anordnung der
Ziffern entsprang den dortigen Vorstellungen.
... ... |
Etwas Nostalgie:
Ich besitze noch einen funktionierenden Tischrechner
von 1971 von Quelle ("Privileg"), der damals fast 300 DM kostete. Er wird
an 220V angeschlossen. Die Ziffern werden mit Glimmlampen angezeigt. Der
Rechner berücksichtigt noch nicht Punkt- vor Strichrechnung, hat aber
schon eine Vornullen-Unterdrückung.
Er ersparte mir seinerzeit viel Rechenarbeit ;-). |
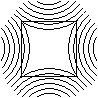
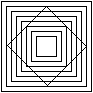
Optische Täuschungen
top
Die linken Quadrate unterscheiden sich in Breite und
Höhe, die rechten in der Größe.
Man ahnt es: Die Quadrate sind gleich groß.
Vier Vierecke liegen vor einer Kreis-,
Quadrat-, oder Geradenschar. Die Seiten sind verzerrt.
Man ahnt es: Bei allen vier Figuren handelt es sich
um Quadrate!
Beide Gitter haben an den Kreuzungspunkten
graue Flecken, links im weißen, rechts im schwarzen Bereich.
Man ahnt es: Die grauen Flecken sind nur Hirngespinste.
Eine Anordnung von vier Dreiviertelkreisen
... ... |
Es wird gar kein Quadrat gezeichnet, trotzdem sieht man
es. |
Spiele mit Quadraten
top
Sieht man sich die gängigen Spiele unter dem Gesichtspunkt
an, ob in ihnen Quadrate in irgendeiner Form vorkommen, wird man fündig.
Fast alle Spiele verwenden Quadrate, sei es als Form des Spielbrettes,
des Spielfeldes oder des Spielsteins.
Ich nenne hier nur die Spiele in alphabetischer Reihenfolge,
die ich an anderen Stellen dieser Homepage beschreibe:
Domino-Puzzle, Fröbelstern,
Fünfzehnerspiel,
Himmel
und Hölle, Magische Quadrate, Mühle,
Rubik's
Magic, Solitär, Tic-Tac-Toe,
Tangram
Das Thema Quadrat
legen findet man an anderer Stelle.
Quadrate
auf meiner Homepage top
Polyominos
Man kann Quadrate zu immer komplexeren
Figuren zusammensetzen. Man fordert, dass sich zwei Quadrate immer in mindestens
einer Seite verbunden sind. Die Figuren hat man gezählt (bis 28-ominos).
Man könnte
sich den Weg zu den Pentominos (Mehrzahl auch Pentominoes) so vorstellen:
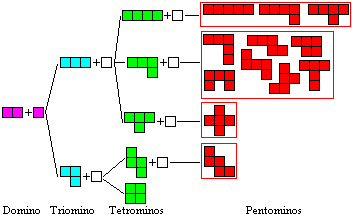
Mehr findet man in meinen Webseiten Domino
Puzzle,
Pentominos und Hexominos.
Lässt man auch Körper zu,
so entstehen Monoide.
... ... |
Als Beispiel werden drei Quadrate vorgegeben. Aus ihnen
lassen sich neben den beiden Triominos acht räumliche Monoide bilden. |
Der bekannteste Monoid ist der Würfel, der aus sechs
Quadraten besteht.
Mehr findet man auf meiner
Seite Rubik's Magic. Mit diesem Puzzle kann man
zahlreiche Körper aus acht Quadraten finden.
Parkettierung
der Ebene
Mehr findet man auf meiner
Seite Homogene Parkettierungen.
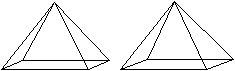
Körper
|
Der Würfel wird von 6
Quadraten gebildet.
Die Bildpaare ermöglichen eine dreidimensionale Sicht. |
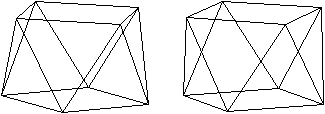
Das größte
Quadrat im Würfel
 |
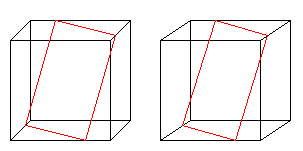Das rote Quadrat ist das größte Quadrat, das
in einen Würfel passt.
Die Eckpunkte des Quadrates teilen die Kanten im Verhältnis
1:3. (Buch 3) |
7 der 13 Archimedischen
Körper werden u.a. von Quadraten begrenzt.
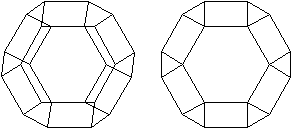
Abgestumpftes Oktaeder
|
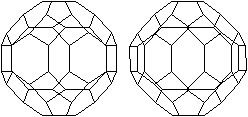
Großes Rhombenkuboktaeder
|
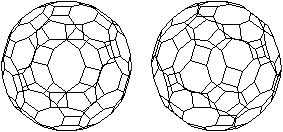
Großes Rhombenikosidodekaeder
|
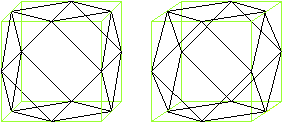
Kuboktaeder
|
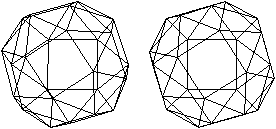
Abgeschrägter Würfel
|
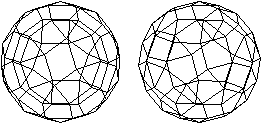
Kleines Rhombenikosidodekaeder
|
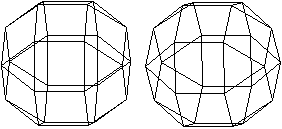
Kleines Rhombenkuboktaeder
Quadrate im Internet
top
Deutsch
Wikipedia
Quadrat
(Geometrie), Quadratur
des Quadrates, Quadratur
des Kreises
Englisch
Eric W. Weisstein (MathWorld)
Square,
Square
Packing,
Perfect
Square Dissection
Erich Friedman
Erich's
packing center
Kevin L. Gong
counting
polyominoes
Wikipedia
Square,
Squaring
the circle
Referenzen top
(1) Walter Lietzmann: Lustiges und Merkwürdiges
von Zahlen und Formen, Göttingen 1969
(2) Friedrich L. Bauer: Einladung zur Mathematik, Deutsches
Museum, München 1999
(3) Martin Gardner: Mathematischer Karneval, Ullstein
Berlin 1977 (Seite 61)
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |
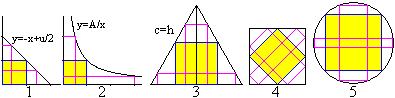
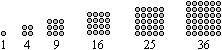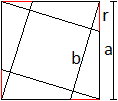