|
Was ist eine Quadratzahl?
Eine Quadratzahl ist eine Zahl, die sich als Produkt
zweier gleicher Faktoren aus natürlichen Zahlen schreiben lässt.
Formeln: k=a*a=a² (k and a stehen für natürliche
Zahlen.)
Danach ist eine Zahl wie 4/9=(2/3)² hier ausgeschlossen.
Umgekehrt entsteht eine Quadratzahl,
wenn man eine natürliche Zahl mit sich selbst multipliziert.
Formeln: a*a=a²=k (k and a stehen für natürliche
Zahlen.)
Der gleiche Faktor heißt Grundzahl.
Das sind die ersten 100 Quadratzahlen.
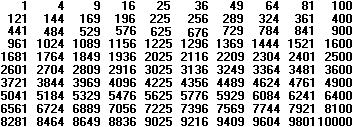
Der Name erklärt sich
aus der Veranschaulichung der Quadratzahlen:
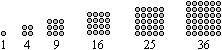
Man stellt fest: In
der Tabelle kommen nur die Einerziffern 0, 1, 4, 5, 6 oder 9 vor.
Dazu eine Überlegung:
Man greift z.B. zunächst die dreistelligen Zahlen
heraus. Sie lassen sich darstellen als 100c+10b+a, wobei a, b und c einstellige
Zahlen sind.
Es gilt (100c+10b+a)² = [(100c+10b)+a]² = (100c+10b)²+2(100c+10b)a+a²
= 100(10c+b)²+10(20c+2b)a+a²
= 10{[10(10c+b)²]+(20c+2b)a}+a².
Das bedeutet, dass sich das Quadrat einer dreistelligen
Zahl in der Form 10x+a² schreiben lässt. Die Einerziffer des
Quadrates wird also allein durch a² bestimmt, und das sind 0,
1, 4, 9 oder die letzten Ziffern von 16,
25, 36, 49,
64 und 81.
Diese Überlegungen können auf alle mehrstelligen
Quadratzahlen übertragen werden.
Quadratwurzel
top
Es ist einfach, eine Quadratzahl zu bestimmen. Es ist
schwieriger, zu einer Quadratzahl die Grundzahl zu finden.
Diesen Vorgang nennt man "Wurzel ziehen" oder radizieren.
Die Bestimmung einer Quadratwurzel ist heute kein Problem
mehr.
Man tippt die Zahl in einen Taschenrechner ein und drückt
die Wurzeltaste: 17424 -- Wurzeltaste -- 132.
An Hand des Beispiels sqrt(17424)
werden weitere Methoden besprochen.
| Statt sqrt(17424) schreibt man bekanntlich auch |
 ......................................................................... |
1 Bestimmung
über eine Intervallschachtelung
Die Zahl muss zwischen 100 und 200 liegen (100²=10000,200²=40000)
Die Zahl liegt zwischen 130 und 140 (130²=16900
und 140²=19600)
Die Einerziffer von 17424 ist 4. Dann kommen nur 132
und 138 in Frage.
Es gilt sqrt(17424)=132.
2 Bestimmung
über eine Faktorenzerlegung
Man zerlegt die Zahl in Faktoren und entwickelt daraus
die Quadratzahl.
17424 = 8*2178 = 16*1089
= 16*9*121. Dann ist die Wurzel 4*3*11=132.
3 Schulmethode
aus vergangenen Zeiten
Auch von der Form her ist es eine
Art schriftliches Dividieren.
1
... ... |
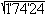Teile die Zahl von rechts aus in Ziffernpaare.
 |
2
... ...
|
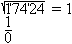Suche die Quadratzahl, die unter oder gleich dem linken
Paar liegt. Das ist hier trivialerweise 01. Subtrahiere die Quadratzahl.
Die Differenz ist 0.
|
3
... ...
|
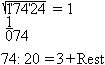Hole das nächste Zahlenpaar ähnlich wie beim
schriftlichen Dividieren herunter. Dividiere in einer Nebenrechnung 074
durch das Zehnfache der verdoppelten Zahl, die oben rechts in der ersten
Zeile steht. Diese Zahl ist 20. Der Quotient ist 3. Der Rest bei der Division
interessiert nicht.
|
4
... ...
|
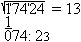Die Nebenrechnung oben nimmt man normalerweise im Kopf
vor. Addiere die dabei gefundene Zahl 3 zum letzten Divisor (20),
und es ergibt sich 23. Schreibe die 3 der Nebenrechnung auch in die ersten
Zeile.
|
5
... ...
|
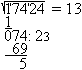Bilde wie beim schriftlichen Dividieren 3*23, schreibe
das Produkt in die nächste Zeile und subtrahiere. Es ergibt sich 5.
|
6
... ...
|
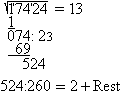Hole das nächste Paar 24 herunter. Dividiere in
einer Nebenrechnung die entstehende Zahl 524 durch das Zehnfache des doppelten
Zahl 13 der ersten Zeile. Das ist 260. Es ergibt sich 2, ein Rest bleibt.
|
7
... ...
|
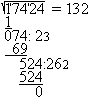Schreibe die Zwei in die erste Zeile rechts und addiere
sie zu 260. Divdiere die Zahl 524 unten durch 262 wie beim schriftlichen
Dividieren. Bilde die Differenz. Sie ist Null.
Es gilt also sqrt(17424)=132.
|
Die Erklärung dieser
Methode ergibt sich aus der "trinomischen Formel" (a+b+c)²=a²+b²+c²+2ab+2ac+2bc.
... ... |
...... |
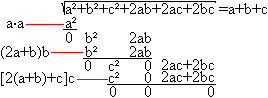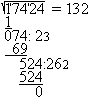Setzt man a=100, b=30 und c=2,
so erhält man das Zahlenbeispiel. |
Mehr findet man auf den Seiten von Andreas Göbel und
Tino Hempel (URL unten).
Bevor es Taschenrechner gab,
war diese Methode die Standard-Methode in der Schule und wurde ausgiebig
geübt. Heute wird sie in manchen Lehrbüchern noch als Unikum
geführt.
(5, Seite 47 "Wurzelziehen per Hand")
4 Bestimmung
nach dem Newtonschen Verfahren
(bzw. Heron-Verfahren)
Bei diesem Verfahren wird mit Hilfe
der konvergenten Folge x1=1 und xk=(xk-1+n/xk-1)/2
die Wurzel x=sqrt(n) immer genauer bestimmt.
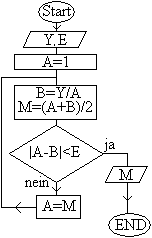
Vielleicht ist es für
Jüngere interessant zu sehen, wie früher das Verfahren programmiert
und veranschaulicht wurde. Die vorherrschende Programmiersprache war in
der 1970er Jahren BASIC.
 |
10 REM ***NEWTON'SCHES NAEHERUNGSVERFAHREN
20 REM ZUR BESTIMMUNG DER QUADRATWURZEL***
30 INPUT Y,E
40 LET A=1
50 LET B=Y/A
60 LET M=.5*(A+B)
70 IF ABS(A-B)<E THEN 100
80 LET A=M
90 GOTO 50
100 PRINT M
110 END |
 |
(6, Seite92f. )
Da staunt man: Erst nach elf Schritten ergibt sich die
Wurzel 132.
Der Grund ist der ungünstige Anfangswert A=1. Er
sollte möglichst nahe an der Wurzel liegen.
Der "Heron-Ansatz" ist A=Y.
Folgen top
Es gibt im Zusammenhang mit Quadratzahlen u.a. fünf
unendliche Folgen. Das sind
>die Folge der natürlichen Zahlen,
>die Folge der Quadratzahlen,
>die Folge der Partialsummen der Quadratzahlen, also
die Reihe der Quadratzahlen,
>die Folge der Kehrwerte der Quadratzahlen,
>die Reihe der Kehrwerte der Quadratzahlen.
Zur
ersten und zweiten Folge
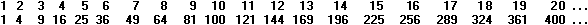Aus den ersten beiden Folgen könnte
man ablesen, dass die Anzahl der Quadratzahlen kleiner ist als die Anzahl
der natürlichen Zahlen. Diese Aussage ist aber falsch. Es gibt nämlich
keine Anzahl "Unendlich". Man könnte eher davon sprechen, dass es
gleich viele natürliche und quadratische Zahlen gibt, denn man kann
jeder natürlichen Zahl eindeutig eine Quadratzahl zuordnen. Man spricht
genauer von gleichmächtig oder äquivalent und bezieht sich mit
diesen Ausdrücken auf die Menge der natürlichen und quadratischen
Zahlen.
Man kann nicht übersehen,
dass es bis zu einer bestimmten Zahl mehr natürliche Zahlen als Quadratzahlen
gibt. Diese Aussage erfasst man in einer ersten Annäherung an das
Problem durch eine Sprechweise die Mengenlehre:
Die Menge der Quadratzahlen ist
eine echte Teilmenge der Menge der natürlichen Zahlen.
Zur
zweiten Folge
Die Folge der Quadratzahlen bezeichnet man auch als arithmetische
Folge zweiter Ordnung.
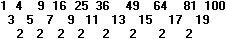Bildet man nämlich die Differenzen zweier aufeinanderfolgender
Glieder der Folge, so ergibt sich eine arithmetische Folge. Sie hat die
Eigenschaft, dass die Differenz konstant ist. Die Folge der Quadratzahlen
hat also konstante "Differenzen der Differenzen".
Die Formel dazu lautet qn-qn-1=2n-1.
Zur
dritten Folge
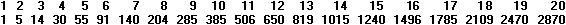Die zweite Zeile erhält man aus den Quadratzahlen durch
Summenbildung:
s1=1²=1
s2=1²+2²=5
s3=1²+2²+3²=14
s4=1²+2²+3²+4²=30, ...
Allgemein gilt sn=1²+2²+3²+...+n²=n(n+1)(2n+1)/6
.
Mögliche Herleitung
| Ansatz: sn=An³+Bn²+Cn |
s1=1 ergibt 1=A+B+C
s2=5 ergibt 5=8A+4B+C
s3=14 ergibt 14=27A+9B+3C |
Daraus folgt
A=1/3, B=1/2, C=1/6 |
Dann ist sn=(1/3)n³+(1/2)n²+(1/6)n =
n(n+1)(2n+1)/6.
(4, Seite 28f.)
Zur
vierten und fünften Folge
Die vierte Folge ist 1/1, 1/4, 1/9, 1/16, ...
, 1/n². Sie hat für n gegen Unendlich den Grenzwert 0.
Interessant ist die zugehörige unendliche Reihe
1/1+1/4+1/9+1/16+,
...
Sie ist konvergent und hat den Grenzwert pi²/6 (nach
Euler) oder gerundet 1,65.
(3, Seite 93f.und Seite 241)
Die entsprechende Reihe gebildet
aus den Primzahlen, nämlich "Summe aus 1/p", ist divergent. Daraus
schließt man, dass die Primzahlen dichter liegen als die Quadratzahlen
(2, Seite 322).
Summen top
Summe der ungeraden Zahlen
Die Summe der ersten ungeraden Zahlen ist eine Quadratzahl.
Genauer gilt 1+3+5+...+(2n-1)=n².
Beispiel: 1 + 3 + 5 + 7 + 9=5².
Differenz
zweier Quadratzahlen
Jede Primzahl p>2 läßt sich eindeutig als
Differenz zweier Quadratzahlen darstellen.
Beispiel: 37=361-324=19²-18²
Division
durch 8
Die Quadrate der ungeraden Zahlen lassen bei Division
durch 8 den Rest 1.
Beispiel: 19² : 8 =361 : 8=45+1/8
Satz
von Lagrange
Jede natürliche Zahl n läßt sich als
Summe von höchstens vier Quadratzahlen darstellen.
Beispiel: 85=64+16+4+1
Fermat-Eulerschsche
Primzahlsatz oder Fermatscher Zwei-Quadrate-Satz
Eine Primzahl von der Form 4n+1 ist als Summe von zwei
Quadraten darzustellen.
Beispiele: 5=1²+2², 13=2²+3², 625=7²+24²=15²+20²
Pythagoräische
Zahlen
Es gibt Zahlentripel, die die Formel a²+b²=c²
erfüllen. Darüber kann man auf meiner Seite 3-4-5-Dreieck
mehr nachlesen.
Zahlenspielereien
top
In diesem Kapitel werden u.a. Ergebnisse aus Lietzmanns
Buch (7) von 1948 zusammengestellt und mit Computerhilfe ergänzt.
Berechnung
von 51² bis 59²
Beispiel: 56²=3136
(50+E)²=(25+E)100+E²
Umsetzung: Addiere zur Einerziffer 25 und hänge
das Quadrat der Einerziffer an.
Berechnung
dreistelliger Zahlen mit einer 0 als Zehnerziffer
Beispiel: 203²=41209, 609²=370881
(H0E)²=H²*10000+2HE*100+E²
Umsetzung: Die beiden Plätze außen werden
von den Quadraten der Hunderterziffer und der Einerziffer gebildet. In
der Mitte steht das doppelte Produkt aus Hunderter und Einer. Ist das doppelte
Produkt dreistellig, so muss zum Quadrat der Hunderter noch der Übertrag
1 addiert werden.
Quadrate
aus den Ziffern 0 bis 9. Jede Ziffer kommt genau einmal vor.
Es gibt 77 Zahlen.
1026 753 849=32043² ist
die kleinste Zahl.
9814072356=99066² ist
die größte Zahl.
Die zehnstelligen Zahlen aus verschiedenen
Ziffern heißen im Englischen "Pandigital numbers".
Quadratzahlen
aus den Ziffern 1 bis 9. Jede Ziffer kommt genau einmal vor.
Zwei Beispiele: 139845276=11826²
und
923187456=30384²
Die neunstelligen Zahlen aus den
Ziffern 1 bis 9 heißen im Englischen "zeroless pandigital numbers".
Spiegelzahlen
12² = 144 und 21² = 441
13² = 169 und 31² = 961 |
102²=10404 und 201²=40401
103²=10609 und 301²=90601
112²=12544 und 211²=44521
113²=12769 und 311²=96721 |
1012²=1024144 und 2101²=4414201
1112²=1236544 und 2111²=4456321
1212²=1468944 und 2121²=4498641
2012²=4048144 und 2102²=4418404 |
Aufeinanderfolgende
Zahlen
| 8281=91² |
183184=428²
328329=573²
528529=727²
715716=846² |
60996100=7810²
82428241=9079²
98029801=9901² |
1322413225=36365²
4049540496=63636² |
Palindrome
unter den Quadratzahlen
121=11²
484=22²
676=26² |
10201=101²
12321=111²
14641=121²
40804=202²
44944=212²
69696=264²
94249=307² |
698896=836² |
1002001=1001²
1234321=1111²
4008004=2002²
5221225=2285²
6948496=2636² |
123454321=11111² |
Fünf
Folgen von Quadratzahlen
1²=1
11²=121
111²=12321
1111²=1234321
... |
4²=16
34²=1156
334²=111556
3334²=11115556
... |
7²=49
67²=4489
667²=444889
6667²=44448889
... |
9²=81
99²=9801
999²=998001
9999²=999800001
... |
13²=169
133²=176 89
1333²=1 776889
13333²=1777 68889
... |
Kaprekarzahlen
Eine Zahl wie 703 heißt Kaprekarzahl,
weil sie folgende merkwürdige Eigenschaft hat:
Quadriert man die Zahl 703²=494209
und teilt das Quadrat in 494 und 209 auf, so ist die Summe 494+209 wieder
703.
Die Kaprekarzahlen unter 10000 sind
1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, 7272,
7777 und 9999.
Figurenzahlen
top
Die Quadratzahlen gehören zu den Figurenzahlen.
Dreieckszahlen
Quadratzahlen
Fünfeckszahlen
Sechseckszahlen
Siebeneckszahlen
Achteckszahlen
...
|
n*(n+1)/2
n²
n*(3n-1)/2
n*(4n-2)/2
n*(5n-3)/2
n*(3n-2)
...
|
1 3 6 10 15 21 28...
1 4 9 16 25 36 49...
1 5 12 22 35 51 70...
1 6 15 28 45 66 91...
1 7 18 34 55 81 112...
1 8 21 40 65 96 133...
...
|
Ein Problem ist es herauszufinden, welche Quadratzahlen in
den übrigen Zahlenfolgen vorkommen.
Bei Mathworld findet man
Quadratzahlen unter den Dreieckszahlen: 1, 36, 1225,
41616, 1413721, 48024900, ... Sloane's A001110
Quadratzahlen unter den Fünfeckszahlen: 1, 9801,
94109401, 903638458801, 8676736387298001, ... (Sloane's A036353)
Mehr über Quadratzahlen steht an anderen Stellen
meiner Homepage.
...
Quadratzahlen
im Internet
top
Deutsch
Andreas Göbel
Ziehen
einer Wurzel - Papier Bleistift Methode
Matheprisma
Quadratzahlen,
Zahlenakrobatik
Tino Hempel
Das
schriftliche Ziehen einer Quadratwurzel
Wikipedia
Quadratzahl,
Quadratwurzel,
Zentrierte
Quadratzahl, Wurzel
(Mathematik),
Schriftliches
Wurzelziehen,
Vier-Quadrate-Satz
Englisch
Eric W. Weisstein (MathWorld)
Square
Number,
Squarefree,
Squareful,
Antisquare
Number, Square
Triangular Number, Pentagonal
Square Number,
Heptagonal
Square Number, Octagonal
Square Number, Square
Root,
Square
Root Algorithms, Newton's
Iteration
Patrick De Geest (World of Numbers)
Extraordinary
squares and powers (non-palindromic allowed)
Neil J. A. Sloane
Integer Sequences
The squares: A000290
Wikipedia
Square
number,
Polygonal_number,
Triangular
square number, Pandigital_number,
9814072356
(number),
Square
root,
Methods
of computing square roots, Euler's
four-square-identity, Kaprekar
number,
Lagrange's
four-square theorem
Referenzen top
(1) Hermann Schubert: Mathematische Mußestunden,
Berlin 1941 (Leitwort: "Ludendo discimus")
(2) Heinrich Behnke u.a.(Hrsg.): Mathematik 1, DAS FISCHER
LEXIKON, Frankfurt am Main 1964
(3) Jean-Paul Delahaye: Pi - die Story, Basel 1999 [ISBN
3-7643-6056-9]
(4) Maximilan Miller: Gelöste und ungelöste
mathematische Probleme, Leipzig 1982
(5) August Schmid u.a.: Lambacher/Schweizer LS9, Stuttgart
1996 [ISBN 3-12-730740-3]
(6) Forsythe, Keenan, Organick, Stenberg: Programmieren
mit BASIC, Braunschweig 1976 [ISBN 3-594-10854-6]
(7) Walter Lietzmann: Sonderlinge im Reich der Zahlen,
Bonn 1948
Feedback: Emailadresse
auf meiner Hauptseite
Diese Seite ist auch in Englisch
vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |
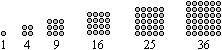
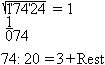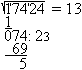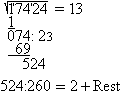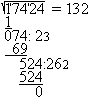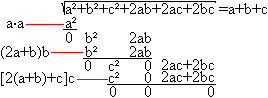