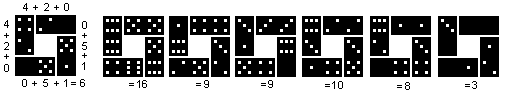|
Was ist Domino? top
 |
Domino ist ein bekanntes Gesellschaftsspiel, bei dem
mindestens zwei Spieler nacheinander sogenannte Dominosteine passend ablegen.
Gewonnen hat, wer zuerst seine Steine abgesetzt hat.
Links eine Darstellung aus der ersten Phase des Spiels. |
Auf das Spiel soll hier nicht eingegangen werden, sondern
auf Puzzles mit Dominosteinen, und dann nur auf Puzzles mit allen 28 Steinen.
Dominosteine top
Für die Dominosteine braucht man acht Folgen von
sieben Quadraten. Das sind insgesamt 56 Quadrate. Sie tragen die Zahlen
0 bis 6. Die Zahlen werden durch Muster dargestellt, wie man sie auf Spielwürfeln
findet. Für die Zahl 0 steht ein leeres Feld (unten links).
Immer zwei Quadrate bilden einen Dominostein (oben rechts).
Das führt zu einer Anzahl von 1+2+3+4+5+6+7=28 Steinen.
Figuren aus Dominosteinentop
Eine beliebte Beschäftigung mit Dominosteinen ist
das Legen von Figuren. Wie beim Dominospiel müssen Steine mit gleichen
Augenzahlen aneinander stoßen. Man beschränkt sich meist auf
symmetrische Muster.
1.Beispiel:
... |
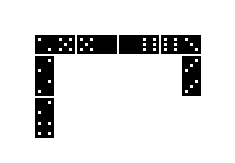
Aus 28 Dominosteinen lässt sich ohne Schwierigkeiten
ein quadratischer Rahmen 15x15 bilden. |
2. und 3. Beispiel: Achsen- und punktsymmetrische
Figuren top
Die Kreuzungen sollte man zuerst legen. Man benötigt
für eine Kreuzung eine ungerade Anzahl von Steinen gleicher Augenzahl.
Folglich müssen Steine mit gleicher Augenzahl auch an einer anderen
Kreuzung verwendet werden, da man auf insgesamt 8 Quadrate (gerade Anzahl)
kommen muss.
4.Beispiel: Eine achsensymmetrische
Figur top
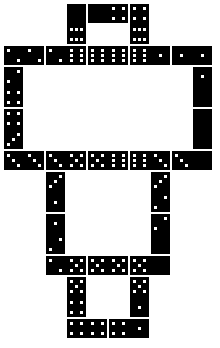
Goliath
|
5. Beispiel: Eine punktsymmetrische
Figur (Buch 2 und Buch 4) top
... ... ... |
Das ist eine bekannte Figur, die man aus allen 28 Dominosteinen
bilden kann.
Man erhält neue Zusammenstellungen, wenn man die
Figur spiegelt oder, das ist interessanter, die Zahlen permutiert. Man
könnte zum Beispiel (0,1,2,3,4,5,6) durch (3,5,1,0,6,2,4) ersetzen. |
... ... ... |
Das ist eine schöne Spielerei.
"MasterTux" stellte mir ein Video
zur Verfügung, das man mit dem VLC-Player oder mit dem Browser Firefox
abspielen kann. |
6.Beispiel: Variante des
dritten Beispiels
... |
Valerio Bianconi aus Italien schickte mir die Lösung
einer neuen Figur. |
Quadrillen top
... ... ... |
Quadrillen gehen auf den französischen Mathematiker
Edouard Lucas (1842-1891) zurück. Das sind kompakte Figuren aus allen
28 Steinen, in denen je zwei 2x2-Quadrate mit gleichen Augenzahlen auftreten.
Hier ein Beispiel! |
Sieben Quadrate top
1.Problem
Man kann aus allen 28 Dominosteinen sieben quadratische Rahmen
legen. Steine stoßen mit gleichen Augenzahlen aneinander.
2.Problem
Man kann aus allen 28 Dominosteinen sieben quadratische Rahmen
so legen, dass auf allen vier Seiten die Summe der Augenzahlen gleich ist
(Buch 1).
Auch der einfache quadratische Rahmen
aus 15x15 Quadraten oben hat die Eigenschaft gleicher Seitensummen. Die
Summe beträgt (1+2+3+4+5+6)*8/4 = 44.
Paare bilden top
 |
Man gibt eine 7x8-Matrix aus den Zahlen 0 bis 6 vor,
jede Zahl kommt achtmal vor. Das sind gerade die Quadrate, aus denen die
Dominosteine bestehen.
Aufgabe ist es nun, aus zwei nebeneinander- oder untereinanderliegenden
Quadraten 28 Dominosteine zusammenzustellen. |
Tipp: Man sollte zunächst die
Dominosteine mit gleicher Augenzahl ("Paschs") herausfinden.
Es folgt eine Lösung.

Dieses Puzzle kann man selbst herstellen.
Dominos im Internet
top
Englisch
James Masters (tradgames.org.uk)
Dominoes
Teun Spaans
Domino
Plaza
Wikipedia
Dominoes
Deutsch
Otto Janko
Domino-Puzzles
Wikipedia
Domino
(Spiel)
Polnisch
Lamiglówki Mix
Domino
Russian
Leonid Mochalov [PUZZLES of LEONID MOCHALOV]
DOMINO
SOLITAIRE, Puzzles
with Dominoes (translated to English)
Referenzen top
(1) Walter Sperling: Auf du und du mit Zahlen, Rüschlikon-Zürich
1955
(2) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1980
(3) Jack Botermans, Pieter van Delft, Rob van den Dobbelsteen:
Denkspiele mit Domino, Würfel und Streichholz, München 1982 (dtv)
(4) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont
taschenbuch1480)
(5) Martin Gardner: Mathematischer Zirkus, Frankfurt
a.M. 1988
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |







 ...
... ...
...
 ...
...