|
Was ist Rubik's Magic? top
...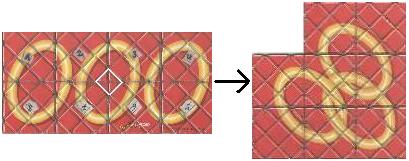 ... ... |
Rubik's Magic ist ein Klappspiel für eine Person,
bei dem man ein Rechteck aus 8=4x2 Quadraten durch eine Folge von Klappungen
in ein Sechseck in Herzform verwandeln soll. |
Dabei müssen sich drei freie Ringe auf der Vorderseite
in drei ineinander verschlungene Ringe auf der Rückseite verwandeln.
... ... ... |
Das erste Magic von Matchbox aus den achtziger Jahren
ist schwarz und hat die gleichen Ringe, ist allerdings schöner wegen
der Regenbogenfarben.
Im Vergleich zur roten Platte steht die schwarze auf dem
Kopf. |
Beschreibung top
.. .... .... |
Wenn man Rubik's Magic kauft, erhält man es als
Platte mit drei Ringen. Die Platte besteht aus acht Quadraten, die mit
Schnüren verbunden sind. Schon nach einigen unbedachten Klappungen
liegen einige Quadrate übereinander. Zieht man die Figur dann auseinander,
ergeben sich die unterschiedlichsten räumlichen Körper,
wobei sich oft einige Quadrate durchdringen. |
... ... ... |
.. .... .... |
Wenn man die Platte auf den Kopf stellt, haben die drei
Ringe die gleiche Position. Um einen dieser beiden Zustände
zu kennzeichnen, nimmt man den Schriftzug "Rubik's Magic" zu Hilfe. Man
nennt Magic aufrecht stehend, wenn die Schrift aufrecht steht. Wie oben
schon gesagt, steht das schwarze Magic aufrecht, wenn die Schrift auf dem
Kopf steht. |
... ... ... |
Die Rückseite von Magic besteht aus ungeordneten
Quadraten. Es gibt dort ein Quadrat, das einmalig ist: Es enthält
drei Bögen. Es wird hier mit Gelb gekennzeichnet. Wird Magic gelöst,
so gelangt dieses Quadrat an eine zentrale Stelle. |
Spielt man mit Magic und will die Züge kontrollieren,
so kann man sich an die Lage des Drei-Bögen-Quadrats halten (Buch
3).
Ich bevorzuge eine Nummerierung aller Platten.
...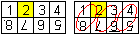 ... ... |
Ich schlage die Nummerierung links vor (ähnlich
wie in Buch 2). So gibt es eine Kette aus acht Quadraten, bei der alle
Zahlen aufrecht stehen. Die Quadrate erscheinen gleichwertig. |
...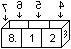 ... ... |
Das zentrale Karo
... ... ... |
Für die folgenden Sequenzen ist die Beobachtung
wichtig.
Unabhängig von Vorder- und Rückseite hat die
4x2-Platte ein Karo aus Rillen in der Mitte auf vier Quadraten gleichzeitig,
in denen Schnüre liegen können. Wenn Schnüre vorhanden sind,
wird das wie rechts markiert. |
... ... ... |
Zugfolgen top
Hat man Magic verstellt, muss man durch Probieren irgendein
4x2-Rechteck finden.
Ist das gelungen, sollte man sich an den folgenden Zugfolgen
versuchen.
Ring

|
Man findet schnell heraus:
Jede Platte kann man zu einem Ring öffnen. |
Austausch
der Zeilen (Sequenz A)
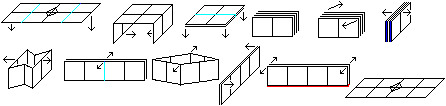
Die Quadrate werden zeilenweise ausgetauscht. Die Schrift
"Rubik's Magic" steht nach wie vor horizontal.
Wiederholt man die Folge, gelangt man wieder zum Ausgangsmuster.
Die Klappfolge hat die Ordnung 2.
Drehung
der Quadrate (Sequenz B)
 Die Quadrate werden gedreht und gleichzeitig
neu angeordnet. Die Schrift "Rubik's Magic" steht nach der Folge
vertikal.
Die Quadrate werden gedreht und gleichzeitig
neu angeordnet. Die Schrift "Rubik's Magic" steht nach der Folge
vertikal.
Wiederholt man die Folge, gelangt man wieder zum Ausgangsmuster.
Die Klappfolge hat die Ordnung 2.
Die Züge sind umkehrbar.
Verwandlung

Übrigens wird das rechte 2x2-Quadrat bei dieser Prozedur
beibehalten.
Alle Muster
aus acht Quadraten top
...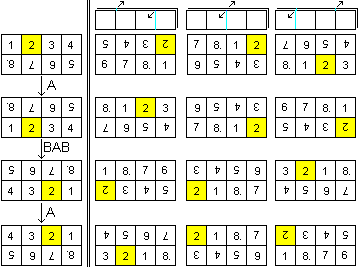 ... ... |
Wie viele Muster kann man mit den Quadraten bilden?
Erste Erkenntnis: Bei jedem Muster bleibt die Reihenfolge
der acht Quadrate erhalten.
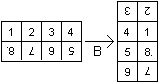
Es gibt vier Hauptmuster (linke Spalte), die durch die
angegebenen Sequenzen A bzw. BAB ineinander übergehen.
Zu jedem Hauptmuster findet man drei weitere (rechte Spalten),
indem man auf das Hauptmuster die unten angegebenen einfachen Zugfolgen
anwendet. |
Ordnen der Quadrate (Sequenzen C1,C2,C3)
 Somit gibt es 16 Muster des 4x2-Rechtecks.
Somit gibt es 16 Muster des 4x2-Rechtecks.
... ... ... |
Wendet man auf das Ursprungsmuster die Sequenz B an,
so gelangt man zu einem 2x4-Rechteck.
Aus Symmetriegründen muss es ebenfalls 16 Rechtecke
dieser Art geben. |
Ergebnis: Insgesamt gibt es 32 Muster des Rechtecks
aus 8 Quadraten.
Eine Lösung top

Erster Schritt
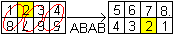
|
Wandele die Platte mit 1 oben links in eine Platte mit
1 unten rechts um. |
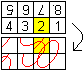
Zweiter Schritt
|
Drehe die Platte um wie links gezeigt. Wende dann die
Transformation an. |
Transformation

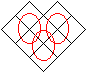
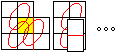
Eine kürzere Lösung
... |
 ... ... |
Wende eine spiegelverkehrte Version der Transformation
auf das Herz an. Mit den Zugfolgen B und C1 gelangt man zu der Platte mit
den drei Ringen.
Der umgekehrte Weg ist eine Lösung. |
Der Klappmechanismus
top
Im ersten Moment glaubt man, dass hier wie beim Spielzeug
Jakobsleiter jedes Stück zwei Scharniere hat. Das ist im Prinzip richtig.
Der Aufbau ist komplizierter.
Legt man zwei Quadrate aufeinander, so entsteht rechtwinklig
zum alten Scharnier ein neues. |
...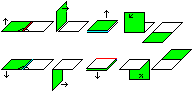 ... ... |
Wo das Scharnier liegt, hängt davon ab, ob man nach
oben oder nach unten klappt und welche Quadrate man klappt. In der Abbildung
liegen zu Beginn die Schnüre vorne, oben.
Das Labyrinth
der Schnüre
top
...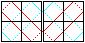 ... ... |
Zwei nebeneinander liegende Quadrate sind mit Nylon-Schnüren
verbunden, die in den Rillen doppelt liegen. Sie verlaufen zum Teil vorne,
zum Teil hinten. Legt man zwei Quadrate aufeinander, so springen beim Klappen
Schnüre in leere Rillen des gegenüberliegenden Quadrats. |
Die folgende Beschreibung
bezieht sich auf den Ring mit den geordneten Quadraten.
...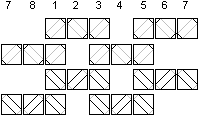 ... ... |
Die acht Quadrate sind durch insgesamt 2x8 doppelt liegende
Ringe miteinander verbunden.
Ein Ringpaar umläuft immer drei Quadrate, wie die
nebenstehende Skizze zeigt. |
In den Rillen der Quadrate 1,3,5 und 7 liegen 2x4 Schnüre,
in den Rillen 2,4,6 und 8 dagegen 2x2. Die Quadrate sind also von
der Konstruktion her nicht gleichwertig.
Beim Klappen müssen immer Schnüre überspringen.
Haben sich die Schnüre an einer Stelle verdrillt, so ist ein Klappen
kaum möglich (passiert!). Man muss Züge dann rückgängig
machen.
Letztes Mittel ist, eine Schnur in einer Rille, in der
zwei Schnüre liegen, durchzuschneiden und zu entfernen. Magic lässt
sich dennoch einwandfrei klappen, sogar leichter. Doch ohne Not sollte
man auf keinen Fall eine Schnur durchschneiden. Doppelt hält besser.
Verschiedene
räumliche Klappformen top
Doppelflächen
... ... ... |
Als Klappformen treten auch ebene Figuren auf, die aus
4+4 Quadraten gebildet werden können. Die T-Form fehlt.
Zieht man diese Figuren auseinander, so ergeben sich
verschiedene Körper. Besonders "L" ist ergiebig. |
Obwohl die Reihenfolge 1 bis 8 der Quadrate erhalten bleibt,
entstehen recht merkwürdige Körper, da sich die Quadrate (auch
mehrfach) durchdringen können.
Würfel
Es ist eine besondere Herausforderung den Würfel
zu falten.
... ....
Vorsichtig! ....
Vorsichtig!
|
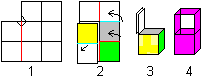
1 Gehe von der Herzform aus. Falte an der roten Linie.
2 Ziehe die Figur auseinander und drehe gleichzeitig.
Achte auf Berge und Täler. Die beiden oberen Quadrate bleiben oben,
die drei rechten Quadrate dreht man nach links vorne.
3 Es entsteht ein Würfel.
4 Man kann oben die Öffnung anheben und erhält
einen Korb. |
... ... ... |
... ... ...
|
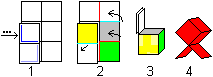
Noch ansehnlicher wird der Würfel, wenn er auf zwei
Quadraten steht.
Die dunkelblauen Linien geben die Lage der Scharniere
an.
Doch der Weg zur Figur 1 ist lang... (Buch 3) |
Symmetrische
kubische Körper
Es gibt viele Körper, auf die man beim Spielen mit
Magic stößt. Wegen der Vielzahl und der "Schönheit" beschränke
ich mich in der folgenden Sammlung auf symmetrische Körper, bei denen
die Quadrate aufeinander senkrecht stehen und die keine Doppelwände
haben.
 Die Körper werden nach zwei Gesichtspunkten geordnet:
Die Körper werden nach zwei Gesichtspunkten geordnet:
(1) Die Farbe kennzeichnet den kleinsten Quader (links),
den man um den Körper legen kann ("Einhüllender Quader").
(2) Die Zahl unter dem Körper ist die Anzahl der
Quadrate, die ein Körper mit dem Quader gemeinsam hat.
Polyominoide top
Man bezeichnet Figuren aus miteinander verbundenen Quadraten,
die in einem kubischen Gitter liegen, Polyominoide.
Jorge L. Mireles Jasso hat sich mit diesen Figuren beschäftigt.
Er bietet im Internet ein Programm an, mit dem man Polyominoide finden,
darstellen und zählen kann (URL siehe unten). Ich habe dieses Programm
auf Figuren aus acht (wegen Magic) Quadraten angewandt.
Man kommt auf die große Anzahl von 207 265 Figuren,
die im Programm nach der Form der umhüllenden Quader geordnet werden.
Es ist verständlich, dass
man mit Magic im Vergleich nur wenige Polyominoide darstellen kann. Die
Einschränkungen sind beträchtlich. Das wird an Quadrat Nr. 3
erklärt, das stellvertretend für eins der acht Quadrate steht.
1.Einschränkung:
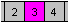
|
Jedes Quadrat hat nur genau zwei Nachbarquadrate. |
Das bedeutet, dass die Reihenfolge der Quadrate erhalten
bleibt.
2.Einschränkung:
...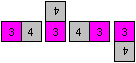 ... ... |
Bei Magic gibt es nur vier Positionen für
ein Nachbarquadrat. Quadrat 4 "rollt" um das Quadrat 3. |
 |
Theoretisch gibt es 16 Positionen, um das Quadrat 4 an das
Quadrat 3 zu legen. Dreht man das Quadrat 4 um, kommt man sogar auf 32
Fälle.
Unmögliche Figuren
top
... ... ...
|
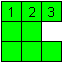
Es ist leicht einzusehen, dass die nebenstehende Figur
nicht mit Magic dargestellt werden kann. Die acht Quadrate bilden keine
fortlaufende Kette. Das Quadrat 3 hat nur einen Nachbarn.
 |
Schwierig ist der nächste
Fall.
... ... ...
|
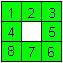
Die acht Quadrate bilden eine Kette und man kann sich
gut vorstellen, dass jeweils drei Quadrate mit Schnüren verbunden
werden können.
Trotzdem gibt es keine Darstellung.
 |
... ... ...
|
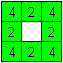
James G. Nourse hat eine Regel für mögliche
und unmögliche Magic-Figuren gefunden. [(3) Seite 18f.]
Die Regel unterscheidet zwischen Quadraten mit vier und
zwei Schnüren.
 |
Regel:
Umlaufe die Figur in einer geschlossenen Linie. Starte
bei einem Quadrat und kehre zu ihm zurück. Bilde dabei schrittweise
eine Summe. Beginne mit der Zahl 0.
>Verlässt man ein Quadrat mit vier Schnüren
und bewegt sich nach rechts, addiere 1, bewegt man sich nach links, subtrahiere
1.
>Verlässt man ein Quadrat mit zwei Schnüren
und bewegt sich nach rechts, subtrahiere 1, bewegt man sich nach links,
addiere1.
>Geht es geradeaus, bleibt die Summe unverändert.
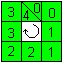
Ist die Summe nach einem vollen Umlauf 0, ist die Figur
mit dem 4x2-Magic lösbar.
... ... ...
|
Hier ist die Summe gleich 4.
 |
Rubik's
Magic Master Edition
top
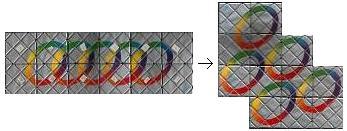 ... ... |
Es gibt eine Version von Magic mit 12 Quadraten.
Viele Züge kann man übertragen, neue sind möglich.
Die Formen sind vielfältiger.
Es gibt ein älteres schwarzes Magic, für das
im Internet Lösungen zu finden sind. Für das graue Magic muss
zu Beginn die Schrift auf dem Kopf stehen. |
Kauf von Rubik's
Magic top
Rubik's Magic gibt es in gut sortierten Spielzeugläden
(Kette "Vedes") und kostet etwa 10€ (2003).
(Copyright Jumbo International, Amsterdam. "Rubik's Cube
is a trademark of Seven Towns Ltd. used under licence".)
Rubik's Magic
im Internet top
Deutsch
Achtziger-forum
Rubik's
Magic
Ronald Bieber
Rubik's
Magic
Wikipedia
Rubik's
Magic
Englisch
Christian Eggermont
Rubik's
Magic
Jaap Scherphuis
Rubik's
Magic Main Page
Maurizio Paolini
A
new topological invariant for the "Rubik's Magic" puzzle
Symmetric
polyominoid configurations
How
to solve Rubik's Magic (Youtube)
Tom Verhoeff:
Minimal
Solutions for the 12 Magic (CFF-nr-16-pp-12-13.pdf)
Magic
and Is Nho Magic (CFF-nr-16-pp-12-13.pdf)
List
of all 1351 Rubik's Magic shapes
Legend: = stands for wrap -2,
- stands for wrap -1, 0 stands for wrap 0,
+ stands for wrap +1, # stands for wrap +2
Wikipedia
Rubik's
Magic, Rubik's
Magic: Master Edition
Youtube
Rubiks
Magic 3 Solutions,
How
to solve a Rubik's Magic,
Rubik's
Magic average 0.86s (Super slow).wmv,
Fixing
a 'Scrambled' Rubik's Magic,
How
to Solve and Re-Scramble Your Master Magic,
Attempting
to Solve the RUBIK'S MAGIC (With NO HELP),
Referenzen top
(1) Christoph Bandelow: Rubik's magische Ringe, Niedernhausen/Ts.
1986
(2) Ashwin Belur, Blair Whitaker: Rubik's Magic, München
1986
(3) James G. Nourse: Simple Solutions to Rubik's Magic,
New York 1986
(4) Wolfgang Glebe: Mathematische Spielereien, Wissenschaftsmagazin
der TU Berlin Heft 10, 1991, Seite 94ff.
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |






 ...
... ...
... ...
... ...
...
 ...
... ...
...

 ...
... ...
... ...
... ....
....
 ...
... ...
...
 ...
... ...
... ...
... ...
... ...
...