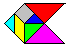
Was ist Tangram?
Tangram ist ein populäres Legespiel.
Aus sieben Steinen, nämlich fünf Dreiecken,
einem Quadrat und einem Parallelogramm, kann man Figuren legen. Dabei müssen
alle Steine verwendet werden. Sie müssen sich berühren, dürfen
sich aber nicht überlappen.
Grundproblem top
| Alle sieben Tangram-Steine bestehen aus kleinen Halbquadraten
der Form |
.. .. |
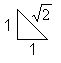Das sind zusammen 32 Halbquadrate oder 16 Quadrate.
... ... |
|
16 Quadrate bilden ein großes 4x4-Quadrat. So ist
das Grundproblem der "Tangram-Forschung" ein Quadrat aus allen sieben Steinen
zu legen. |
Anmerkung:
Man kann auch den kleinsten Tangramstein (blaues Dreieck)
als Grunddreieck annehmen. Ich verwende das halbe Dreieck als Grundelement,
denn dann hat das Quadrat aus den sieben Tangramsteinen die einfache Länge
4.
| Grunddreieck auf dieser Seite: |
...... |
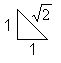Andere Möglichkeit: |
 . |
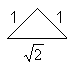Unterschied: Rationale und irrationale Seitenlängen
sind vertauscht.
Figuren legen
1.Problem: Neue Figuren legen top
... ... |
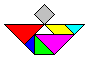Man kann neue Figuren erfinden.
Die Figuren sollten so beschaffen sein, dass man schon
auf den ersten Blick erkennt, was dargestellt wird.
Es gibt Tausende von Figuren, die schon mit den Steinen
gelegt worden sind. |
... ...
|
[3sqrt(2)]x[3sqrt(2)]-Quadrate sind möglich, wenn
man einen oder zwei Steine auslässt.
 |
2.Problem: Auslegen von vorgegebenen
Silhouetten
top
..... ..... |
Es ist gar nicht so leicht, vorgegebene Umrisse von Figuren
mit den Tangram-Steinen auszufüllen. (Lösung am Ende dieses Kapitels) |
3.Problem: Wie viele Möglichkeiten
gibt es, eine Figur zu legen?
top
... ...
|
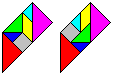
Das Trapez kann auf zweierlei Weise ausgelegt werden.
Sicher gibt es noch mehr Möglichkeiten. |
Paradoxa
... ... |
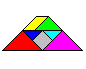Das nebenstehende gleichschenklige Trapez ist nicht möglich.
Legt man die Figur mit Tangram-Steinen nach, so erkennt
man einen Fehler:
Der gelbe und der grüne Stein sind ein wenig größer
als gezeichnet.
Man benutzt hier den Sachverhalt, dass 4 und das Dreifache
der Wurzel aus 2 (=4.24) in etwa übereinstimmen. |
 |
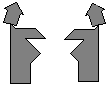Andere Paradoxa vergleichen zwei scheinbar gleiche Tangramfiguren.
Ein Beispiel von H.Dudeney
|
Lösung:
 |
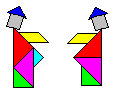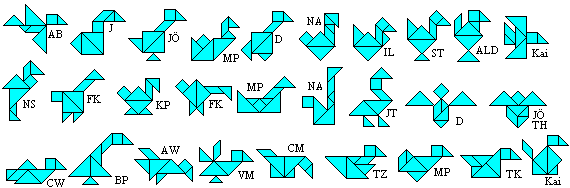
Tangram-Vögel top
Etwa 100 Schülerinnen und Schüler (11/12/13
Jahre alt) erhielten den Auftrag Vögel zu entwerfen.
Hier aus Platzgründen nur eine Auswahl schöner
Vögel:
Nicht alle Schüler konnten sich mit den Tangram-Steinen
anfreunden:
 ;-)
(Dank an 6b, 6c, 7a, 7c, 7d in 1999/2000)
Paul's
Men
Mein Enkel Paul (11) schickte mir die folgenden Figuren
für diese Seite.
Ordnen der
Tangram-Figuren
top
Man kann sich z.B nach der Lage der Seiten eines Halbquadrates
richten.
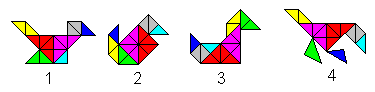1 Katheten horizontal oder vertikal
2 Hypotenuse horizontal oder vertikal
3 Mischung aus 1 und 2
4 Lage der Dreiecksseiten beliebig
Vom mathematischen Standpunkt aus sollte man nur die Figuren
1 und 2 zulassen.
Fast alle Tangramfiguren aber sind vom Typ 4. Da es hier
keine festen Regeln gibt, entstehen viele schöne und ausdrucksstarke
Formen. - Sie werden üblicherweise nach Themen geordnet.
Konvexe Figuren top
Eine Figur ist konvex, wenn sie nur nach außen
gewölbt ist. Genauer: Greift man zwei beliebige Punkte innerhalb der
Figur heraus, so liegt auch die Strecke zwischen den beiden Punkten innerhalb
der Figur.
 |
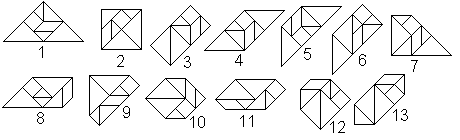Es gibt erstaunlicherweise nur 13 konvexe Figuren, die
man mit Tangram-Steinen legen kann. |
Beweis durch Fu Traing Wang und Chuan-Chih Hsiung 1942 (Buch
4)
Gitternetz-Tangrams
mit konvexer Schale top
 |
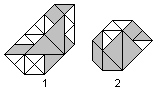In Buch 3 und 4 findet man einen interessanten Vorschlag,
Tangramfiguren zu klassifizieren.
Es geht aber nur um 'mathematische' Tangramfiguren,
für die die Vögel 1 und 2 oben als Beispiele stehen. Sie
können so in ein Koordinatensystem gelegt werden, dass die Eckpunkte
der Tangramsteine ganzzahlige Koordinaten haben. Anders ausgedrückt:
Die Tangramsteine können so gelegt werden, dass die Hypotenuse die
Einheit 1 bekommt und horizontal oder vertikal liegt. Strecken mit der
Einheit (Wurzel aus 2) liegen schräg. - Entsprechend wird Vogel 1
gedreht. |
Die Figuren werden sodann durch möglichst wenige (weiße)
Dreiecke ergänzt, so dass eine konvexe Figur entsteht. Diese Dreiecke
entsprechen der Größe der blauen Tangramsteine. Die Dreiecke
werden gezählt. Der Vogel 1 benötigt 14 Dreiecke und ist 14-konvex,
Vogel 2 ist 5-konvex. Die konvexen Figuren oben benötigen kein Dreieck
und sind demnach 0-konvex. Im Buch 4 werden sämtliche 133 (abstrakten)
1-konvexen Tangramfiguren abgebildet und gelöst.
Es gibt das Problem, eine Figur mit
einer möglichst großen, konvexen Schale zu finden.
Bruno Curfs fand die folgenden sieben 41-konvexe Tangrams
(5). Wahrscheinlich ist 41 die obere Grenze.
...
... ... |
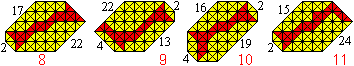Ich erhielt weitere 41-konvexe Tangrams: 8 von Ludwig
Welther, 9 von Hartmut Blessing,
10 und 11 von Hannes Georg Kuchler. |
... ... |
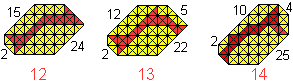Daniel Gronau teilte mir mit, dass er alle möglichen
Gitter-Tangrams durchrechnen ließ. Er stellte fest, dass es noch
drei weitere Lösungen gibt. |
Bruno Curfs weist mathematisch
nach, dass 44-konvex eine obere Grenze ist (5).
Herstellung
von Tangram-Steinen
top
Wahrscheinlich sind die Tangram-Steine dadurch entstanden,
dass man ein 4x4-Quadrat zerschnitten hat.
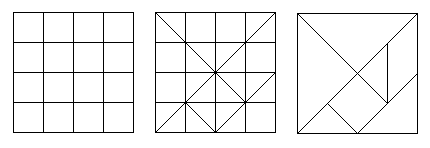Das macht man sich bei der Herstellung der Tangram-Steine
zunutze. Man zeichnet auf Sperrholz oder auf Pappe ein 4x4-Quadrat mit
etlichen Diagonalen. Dann zersägt bzw. zerschneidet man das Quadrat
wie oben angegeben.
ALOIS STUDER HAT DIE SIEBEN TANGRAMTEILE GEKLÖPPELT.
|
Engel
|
Alois Studer sandte mir jetzt
(Juli 2020) eine weitere, kunstvoll geklöppelte Arbeit zu. Er nennt
sie Tangram hoch 2.
Sie ist insofern sehr interessant, dass er ein Quadrat
aus zwei großen, drei mittleren und zwei kleinen Tangramsätzen
bildete.
Varianten
des Tangram-Spiels
top
Man erzeugt weitere Tangramspiele, indem man einfache geometrische
Figuren wie Quadrat, Rechteck oder Kreis aufteilt. Die bekanntesten sind
(1) "Pythagoras", (2) "Kreuzbecher", (3) "Alle Neune", (4) "Kreis-Rätsel",
(5) "Das gebrochene Herz"
und (6) "Das magische Ei".
Hier ist ein weites Feld weitere eigene Tangramsteine
zu entwerfen und mit ihnen zu spielen.
Tangram im Internet
top
Deutsch
Claus Michael Ringel
Tangram
Gerd Müller
Tangram
interaktiv
Herbert Hertramph
Tangram-Spiel
von Jos van Uden, Tangram-Spiel
von Serj Dolgav zum Herunterladen
Michael Bischoff
Tangram for you
stopkidsmagazin
Tangram
online
tan-gram
tangram mit einer
galerie von 75 exponaten
Wikipedia
Tangram
Englisch
Andrew D. Orlov
Tangram
House
Barbara E. Ford
Tangrams - The Magnificent
Seven Piece Puzzle
Gianni A. Sarcone and Marie-Jo Waeber
Tangram,
the incredible timeless 'Chinese' puzzle
Marie-Jo Waeber and Gianni A. Sarcone (Archimedes'
Laboratory)
Tangramagic
Michael Bischoff
Tangram for you
Paul Scott
CONVEX
TANGRAMS
Wikipedia
Tangram
Referenzen top
(1) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1998 ISBN 3-88034-87-0]
(2) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont
taschenbuch1480) [ISBN 3-7701-2097-3]
(3) Rüdiger Thiele, Konrad Haase: Teufelsspiele,
Leipzig 1991 [ISBN 3-332-00116-7]
(4) Joost Elffers, Michael Schuyt: Tangram, Dumont, Köln
1997
(+ Tangramsteine) [ISBN 3-7701-4089-3]
(5) Bruno Curfs: Mathematical Tangram, CFF, newsletter
of the "Nederlandse Kubus Club" NKC, 65 (November 2004)
(6)Jerry Slocum, Dieter Gebhardt, Jack Botermans, Monica
Ma, Xiaohe Ma: The Tangram Book, 2003
[ISBN 1-4027-0413-5] Sterling
Publishing Company
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |
