|
Was heißt Quadrate legen?
Es geht um Puzzles, bei denen man aus gleichen oder verschiedenen
Stücken ein Quadrat legen soll.
Ein erstes Beispiel ist das
Tangram-Spiel.
Man zerlegt ein Quadrat (1) in sieben Teile (2) und - das
ist das Puzzle - setzt sie wieder zu einem Quadrat zusammen (3). In diesem
Falle ist es auch möglich, Quadrate mit einem oder zwei Löchern
zu legen (4).
2.Beispiel
Es gibt viele Puzzles, bei denen eine Figur zerlegt und
dann zu einem Quadrat zusammengesetzt wird.
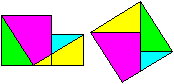
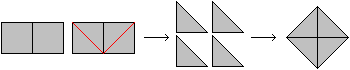Hier wird ein Doppelquadrat in vier gleiche Teile zerlegt
und zu einem Quadrat zusammengesetzt.
Quadrate zerlegen top
Es folgen einige Aufteilungen von Quadraten. Wenn man
will, kann man die Figuren auf kariertes Papier übertragen, auf Pappe
kleben und ausschneiden. So erhält man einfache Puzzles.
Beschreibungen:
1 Mit vier Schnittlinien erhält man 8 gleichschenklig-rechtwinklige
Dreiecke.
2 Mit drei Schnittlinien erhält man vier
1-2-sqrt(5)-Dreiecke.
3 Mit zwei Schnittlinien ergeben sich zwei Quadrate
und zwei kongruente Rechtecke. Zur Zerlegung gehört die binomische
Formel (a+b)²=a²+2ab+b².
4 Vier L-Tetrominos bilden ein Quadrat.
5 Vier T-Tetrominos bilden ein Quadrat.
6 Man trägt von jeder Ecke aus in eine Richtung
die Strecke e ab und verbindet die gegenüberliegenden freien Endpunkte
dieser Strecken. Es entstehen vier kongruente Vierecke mit rechten Gegenwinkeln.
7, 8, 9 Drei Aufteilungen aus Buch (5).
Das hat man als Kind vielleicht schon
einmal gemacht und das sollte hier nicht fehlen:
Man zerschneidet ein Quadrat, besser ein quadratisches
Bild, nach Belieben.
Figuren zerlegen top
Die folgenden Figuren kann man so zerlegen, dass man
die Stücke zu einem Quadrat zusammensetzen kann. (Dieses ist nur eine
kleine Auswahl.)
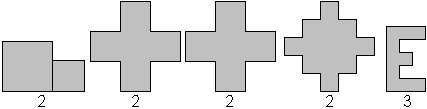Wer will, kann sich an den Figuren selbst versuchen. Unter
den Figuren steht die Anzahl der Schnitte. Die Lösungen sind nicht
immer einfach zu finden.
Lösungen
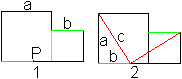
Zwei Quadrate
Man trägt die Seite b des kleineren Quadrates auf der
Seite a des größeren Quadrates ab. Es entsteht Punkt P. Diesen
Punkt verbindet man mit den oberen Eckpunkten der Quadrate.
Die Figur ist unter dem Namen "Stuhl der Braut" bekannt.
(siehe auch
Formeln im Bild)
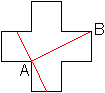
Griechisches
Kreuz 1
Man verbindet die Eckpunkte A und B und zeichnet durch
Punkt A die Senkrechte zu AB.
(1, 28.April), (2, Problem 34), (4, Seite 29)
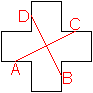
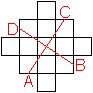
Griechisches
Kreuz 2
Man halbiert vier sich entsprechende Seiten und verbindet
gegenüberliegende Halbierungspunkte.
(2, Problem 34), (4, Seite 29)
13-Quadrate-Figur
Man halbiert vier sich entsprechende Seiten und verbindet
gegenüberliegende Halbierungspunkte.
(1, 3.July), (3, Seite122)
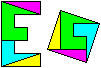
Buchstabe E
Man zeichnet drei Diagonalen. - Legt
man ein Quadrat, muss man zwei Stücke umdrehen bzw. spiegeln.
(3, Seite 52 und 117), (4,
Seite 36)
Anmerkung:
Diese Puzzles haben den folgenden
mathematischen Hintergrund:
Man kann jedes Polygon in ein flächengleiches
Quadrat verwandeln. Dazu zerlegt man das Polygon in Dreiecke, die man in
ein Parallelogramm, dann ein Rechteck und schließlich in ein Quadrat
verwandeln kann.
Der dreidimensionale Fall, nämlich
ein Tetraeder in einen volumengleichen Würfel zu verwandeln, ist nicht
lösbar (Problem 3 bei David Hilbert, siehe Linkliste).
Treppenfigur
... ... |
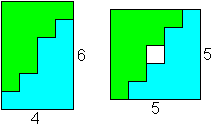Denksportaufgaben, bei denen eine Treppenkurve zu einer
Lösung führt, findet man häufiger. Hier ein Beispiel. |
(1, 20.Mai)
Von der Vase
zum Quadrat
... ... |
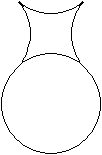Sechs Viertelkreise bilden eine Vase.
Aufgabe:
Die Figur soll durch zwei gerade Schnitte so aufgeteilt
werden, so dass man aus den Stücken ein flächengleiches Quadrat
legen kann. |
Lösung |
Mitgeteilt von Dietmar Viertel
Vom
Kreis zum Quadrat
... ... |
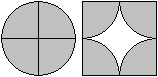Es wird ein Kreis in ein Quadrat verwandelt.
Wenn man die Aussage weglässt, dass die Flächeninhalte
gleich sein sollen, so ist dieses eine Scherzlösung der Quadratur
des Kreises. |
Trugschlüsse top
Schachbrett-Paradoxon
Die folgende Figur ist sehr bekannt.
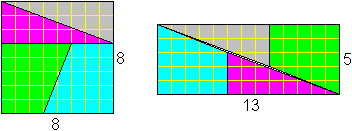Das Problem liegt darin, dass ein Quadrat mit den Maßen
8x8=64 zerschnitten wird und das Rechteck, das man aus den vier Stücken
legen kann, dann die Maße 13x5=65 hat. Woher kommt der Unterschied
65-64?
Oben wurden die vier Stücke isoliert, gedreht und
zu einem Rechteck zusammengeschoben. Guckt man genau hin, so ist die "Diagonale"
des Rechtecks doppelt. Diese Aussage wird oft verschleiert, indem man nur
die übliche Diagonale des Rechtecks zeichnet. Wenn man will, kann
man den Trugschluss auch durch Rechnung mit einer Winkelbetrachtung aufdecken.
(3), Seite 97 und 132/133
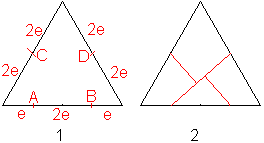
Vom gleichseitigen
Dreieck zum "Quadrat"
Man teilt die Grundseite in vier gleiche Teile und halbiert
die anderen. Man erhält die vier Punkte E, F, A und B. Dann verbindet
man E und B und fällt von den Punkten A und E die Lote auf FB. So
entsteht Figur 2.
Aus den vier Teilen des Dreiecks legt man ein "Quadrat".
Genau genommen ist aber kein Quadrat
entstanden. Das zeigt die folgende Rechnung.
Es wird gezeigt, dass die beiden im Quadrat unten liegenden
Seiten 2AD und DB+CB nicht gleich lang sind.
... ... |
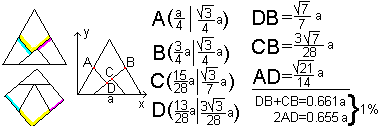Sie werden im gleichseitigen Dreieck mit Farbe gekennzeichnet.
Man legt das Dreieck in ein Koordinatensystem und bestimmt
die Länge dieser Strecken.
Es zeigt sich, dass sie sich nur um 1% unterscheiden. |
Diese Zerlegung geht auf H. E. Dudeney (1847-1930)
zurück. Dudeney hat allerdings die Grundseite nicht wie eben beschrieben
in 1:2:1 geteilt. Er hat die Teilpunkte unten so gelegt,
dass Dreieck und Quadrat exakt den gleichen Flächeninhalt haben. Das
Teilungsverhältnis ist angenähert 0,98:2:1,018.
Würfel bauen top
Das Problem "Quadrate legen" kann auf die dritte Dimension
übertragen werden.
Dann heißt es "Würfel bauen". Es folgen drei
Beispiele, die an anderer Stelle abgehandelt werden.
Quadrate
legen im Internet top
Englisch
Ina Kersten
Hilbert's
Problems
Eric W. Weisstein (Mathworld)
Dissection
Torsten Sillke
Geometrical
Paradox ("A Chessboard Paradox")
Wikipedia
Dissection
puzzle
Deutsch
Ina Kersten
Hilberts
Mathematische Probleme
A. Schreiber, T. Ehmke
Dudeney-Puzzle
Französisch
Th. Eveilleau
Le
découpage de Dudeney (L'animation, Le secret du découpage,
Théorème général)
Referenzen top
(1) PAST TIMES: 366 BAFFLING BRAIN TEASERS & CUNNING
CONUNDRUMS FOR EVERY DAY OF THE YEAR, Oxford 1999
(2) Sam Loyd, Martin Gardner: Noch mehr mathematische
Rätsel und Spiele, Köln 1979 [ISBN 3-8321-1145-x]
(3) Heinz Haber: Mathematisches Kabinett, dtv 10121,
München 1967 und 1970 [ISBN 3-423-10121-0]
(4) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1998 [ISBN 3-88034-87-0]
(5) Anthony S. Filipiak: Mathematical Puzzles and other
Brain Twisters, New York MCMXLII
Kommentar top
In einer Mathematik-Ecke des Museums "Universum" in Bremen
liegen Dudeneys Figuren als Holzstücke aus (November 2003). Sie haben
mich veranlasst, dieses schöne Problem weiter zu verfolgen. So entstand
diese Seite. - Übrigens ist in diesem empfehlenswerten Museum ein
besonderes Highlight der Irrgarten für Kinder.
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2004 Jürgen Köller
top |
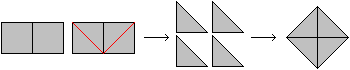
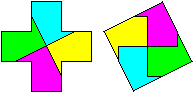
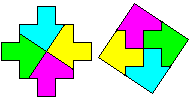
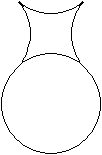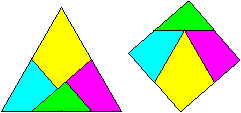
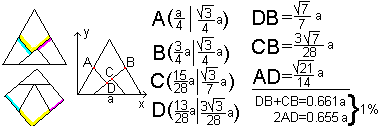