|
Was ist der Origami-Würfel?
... |
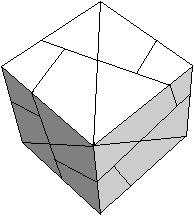
Der Origami-Würfel ist ein Würfel, der aus
einem quadratischen Blatt Papier gefaltet wird.
Er heißt auch Aufblasbarer Würfel oder
Wasserbombe. |
Als diese Seite 1999 entstand,
kannte ich nur diesen Würfel, der aus einem Quadrat gefaltet wird.
Jetzt (2024) stelle ich unten weitere Würfel vor.
Bau eines Origami-Würfels
top
01
...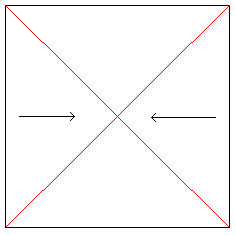 ... ... |
Falte und entfalte ein quadratisches Blatt Papier an
beiden Diagonalen.
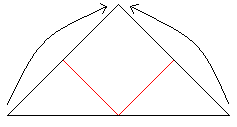
Schiebe das Quadrat so zusammen, dass die beiden Pfeile
übereinanderliegen. Lege die Dreiecke oben und unten aufeinander. |
02
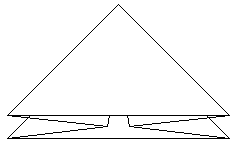 |
Es entsteht das 'Fliegerdreieck', das von der Papierschwalbe
her bekannt ist. |
03
 |
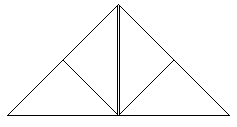
Falte die Ecken unten rechts und links zu der Ecke oben
Mitte. Die rote Linie ist die Faltlinie.
 |
04
 |
Danach müsste das so aussehen........................................................................................ |
05
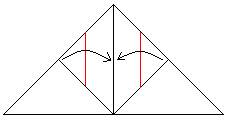 |
Falte die kleinen Dreiecke zur Mitte hin......................................................................... |
06
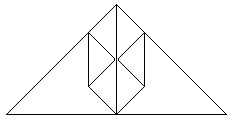 |
Danach müsste das so aussehen.................................................................................... |
07
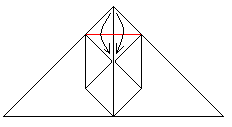 |
Klappe die beiden kleinen Dreiecke an der roten Linie
nach unten.................................... |
08
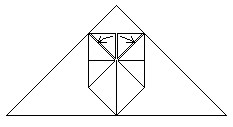 |
Stecke die zuletzt erzeugten Dreiecke in die beiden Taschen
rechts und links.
Das ist etwas knifflig..................................................................................................... |
09
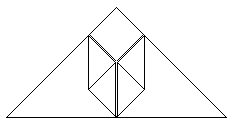 |
Danach müsste das so aussehen.................................................................................... |
10
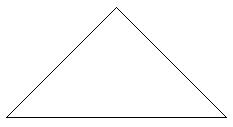 |
Drehe das Gebilde um und führe die Schritte 3,4,5,6,7,8,9
durch................................... |
11
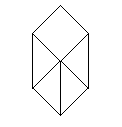 |
Danach müsste das so aussehen...................... |
12
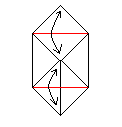 ............. ............. |
Falte an den roten Linien. Mache die Faltungen wieder
rückgängig. |
13
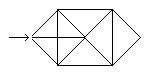 ....... ....... |
Führe den noch zusammengefalteten Würfel zum
Mund,
puste kräftig in das Loch an der Spitze und entfalte
so den Würfel. |
14
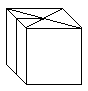 |
Der Würfel ist fertig.................... |
Etwas Mathematik top
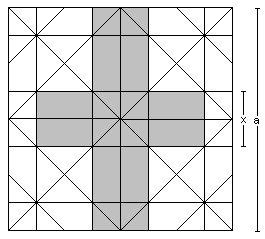 ... ... |
Nimmt man den gefalteten Würfel auseinander, so
erhält man ein schönes Muster, das durch die Faltlinien erzeugt
worden ist.
Es gilt:
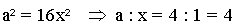
|
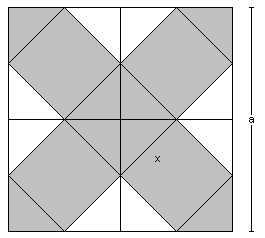 |
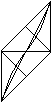
Das größte Netz eines Würfels, das noch
in ein Quadrat passt, ist links abgebildet.
Es gilt:
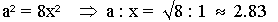
Der Würfel wird wesentlich größer als
der gefaltete Würfel. |
Soll die gesamte Quadratfläche
für einen Würfel verwendet werden, so gilt:
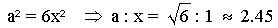 Das ist der größtmögliche Würfel, theoretisch.
Das ist der größtmögliche Würfel, theoretisch.
Näheres dazu in Buch (5), Seite 63f. und Seite 71ff.
"Der eingewickelte Würfel".
Weitere
Origami-Würfel aus einem Quadrat top
Das Falten von Würfeln ist
offenbar eine weit verbreitete Kunst. Im Internet gibt es bei Youtube zahlreiche
Anleitungen.
Ich habe mich umgesehen und elf
weitere Würfel - gefaltet aus einem Quadrat - gefunden.
...
Es sei a die Seitenlänge
des Ausgangsquadrates und x die Kantenlänge des Würfels.
01
Origami Cube (Shuzo Fujimoto)
Eine Anleitung findet man - falls
nötig - unter "01 Youtube"
(URL unten).
... ... ... |
Es ist möglich, einen Würfel aus einem quadratischen
Blatt Papier zu falten.
Er hat vier glatte Quadrate als Seitenflächen.
Zwei gegenüberliegende Seitenflächen zeigen
die Diagonalen. |
...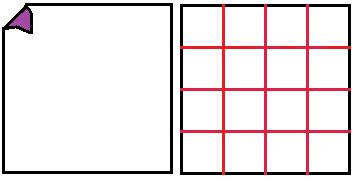 ... ... |
Zum Bau benötigt man z.B. ein Quadrat 15cm x 15cm
aus Origamipapier.
Man erzeugt zunächst durch Falten ein Gitter 4x4.
Dabei sollte man darauf achten, dass die Faltlinien nur
locker festgelegt werden. |
...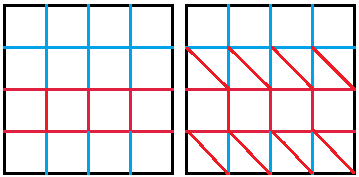 ... ... |
Erst in einem zweiten Schritt werden die Faltlinien z.B.
mit dem Fingernagel nachgezogen, und zwar nach einem Muster, das in der
nebenstehenden Zeichnung angegeben ist.
Talfaltungen sind rot markiert, Bergfaltungen blau.

|
...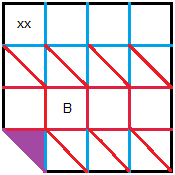 |
Die untere linke Spitze wird umgeknickt, die Farbe der
Rückseite wird sichtbar.
Zwei Quadrate werden mit B und xx gekennzeichnet. |
...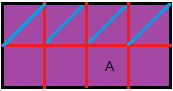 .... .... |
Dann wird an der Mittellinie nach unten gefaltet. Ein
Quadrat bekommt die Kennzeichnung A.
Jetzt wird es dreidimensional. Man schiebt das Quadrat
A auf das Quadrat B so, dass die Buchstaben aufrecht stehen bleiben und
übereinander liegen. Berg- und Talfaltungen müssen beachtet werden. |
... .. .. |
So sieht die Faltarbeit aus, wenn man A auf B schiebt................................................................... |
..... . . |
Das Quadrat xx schiebt man unter das violette Quadrat
darunter.
Man kann eine Seitenfläche des Würfels mit den
sichtbaren Diagonalen formen. |
... ... ... |
Man schließt die gegenüberliegende Seitenfläche,
indem man den Faltlinien folgt.
a = 4x oder x = 0,25a |
02
Origami Seamless Cube
Eine Anleitung findet man unter
"02 Youtube" (URL
unten).
The Seamless Cube (der nahtlose
Würfel) hat sechs glatte Quadrate.
... ... ... |
Geht man vom fertigen Würfel zum Quadrat zurück,
ergibt sich das nebenstehende Bild.
a = 4x oder x = 0,25a
|
... ... ... |
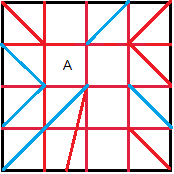
Ein nicht leichter Schritt ist, das vorgefaltete Quadrat
zu einem Würfel zu formen.
Das Quadrat oben mit dem Buchstaben A ist der Boden.
Ist der Würfel gelungen, so schauen oben drei Spitzen
heraus, die von einer Ecke ausgehen.
Sie werden in bereit stehende Taschen gesteckt. |
03
Würfel mit Deckel
Eine Anleitung findet man unter
"03 Youtube"
(URL unten)
.. . . |
Wenn man an diese Stelle angekommen ist, muss man die
Seitenlänge dritteln.
Das erreichen geübte Falter durch Falten.
Das Dritteln gelingt besser, wenn man mit Hilfe eines
Maßstabes mindestens eine Markierung einzeichnet. |
... ... ... |
In dieser Phase hat die Faltarbeit
zwei potentielle Deckel.
Man kann einen in den Würfel
schieben und erhält einen Würfel mit einem Deckel. |
... |
Will man einen glatten Würfel erzeugen, muss man
die Deckel ineinander schieben.
Den Zipfel oben rechts kann man
verschwinden lassen. |
...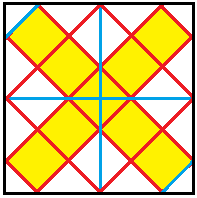 |
Geht man vom fertigen Würfel zurück auf das
Quadrat, ergibt sich das Bild links.
a = 3sqrt(2)x or gerundet x = 0,24a |
04
ORIGAMI SEAMLESS CUBE (Jo Nakashima)
Eine Anleitung - wenn nötig
- findet man unter "04 Youtube"
(URL unten).
... |
Der Weg zu diesem glatten Würfel ist leicht zu verstehen.
Man faltet eine Röhre aus drei Würfeln, wobei
die Enden offen sind.
Die Öffnungen verschließt man mit den äußeren
Würfeln. |
... |
Man benötigt ein 5x5-Gitter. Entweder zeichnet man
es oder faltet es wie im Video. |
...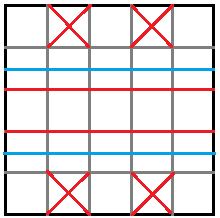 |
In einem ersten Durchgang gibt man vier Quadraten ein
Kreuz als Talfaltungen.
Weiter folgen horizontal liegend zwei Tal- und zwei Bergfaltungen. |
...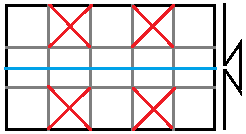 |
So ist es möglich, das Quadrat zusammen zu schieben,
so dass die Bergfaltungen aneinander stoßen. |
...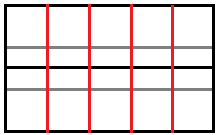 |
Vier Talfaltungen ermöglichen es, eine "Röhre"
zu bilden. |
... |
Man schiebt den mittleren Wulst ineineinander. |
... |
Dann verschließt man die Öffnungen wie links
und bildet Zipfeln wie im Foto rechts. |
... |
Die vier Zipfel schiebt man in die Taschen außen.
Das ist mühsam. Es gelingt besser, wenn man die
Faltungen der Zipfel noch einmal schärft.
a = 5x oder x = 0,2a |
05
Origami Gift Box
Eine Anleitung findet man unter
"05 Youtube"
(URL unten).
.... .. .. |
Dieser Würfel ähnelt Würfel 04.
Auch hier geht man über eine Röhre aus drei Würfeln.
Der Unterschied ist der, dass die Öffnungen einfacher
geschlossen werden, nämlich wie in der Endphase von Würfel
01. Es entsteht kein glatter Würfel, sondern - gegenüber
liegend - sind Diagonalen zu sehen. |
.... .... ....
01
|
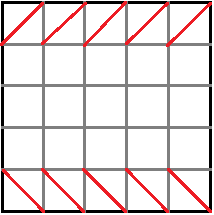 .... ....
05
|
Da sieht man den Unterschied zwischen
Würfel 01 und Würfel 05.
a = 4x oder x = 0,25a |
... ... ... |
Das muss man wissen:
Da, wo zwei Quadrate oben übereinander liegen, muss
man beim Schließen nur das innere Quadrat nach unten in den Würfel
drücken. |
06
Origami Gift Box / Ring Box Puzzle
Eine Anleitung findet man unter
"06
Youtube"
(URL unten).
... ... ... |
Da wird der fast gleiche Würfel wie 06
vorgestellt, nur hat der fertige Würfel in der Mitte eine Rille, weil
die Röhre anders herum gefaltet wird.
a = 4x oder x = 0,25a |
07
Vierstrahliger Würfel
Eine Anleitung findet man unter
"07
Youtube"
(URL unten).
...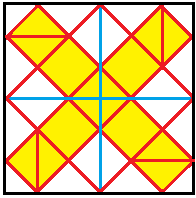 |
Das ist eine naheliegende Methode, einen Würfel
aus einem Quadrat zu falten.
Man erkennt das Netz des Würfel, wobei für den
Deckel vier Quadrate untergebracht werden.
Die weißen Quadrate verschwinden im Inneren.
a = 3sqrt(2)x oder gerundet x = 0,24a |
... |
Es ist schwierig, die vier Zipfeln zu bilden, aber machbar.
Die Zipfel werden übereinander gelegt, der letzte
wird weggesteckt. |
08
Origami Gift Box with one piece of paper
Eine Anleitung findet man unter
"08 Youtube"
(URL unten).
... |
Das ist der Moment, ab dem nicht mehr gefaltet werden
muss.
Es wird dann dreidimensional |
... ... ... |
 ... ... |
Der Würfel besteht aus zwei Hälften.
In Ruhestellung ist er ein wenig geöffnet. |
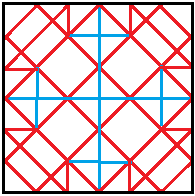 |
Geht man vom fertigen Würfel zurück auf das
Quadrat, ergibt sich das Bild links.
a = 3sqrt(2)x or näherungsweise x = 0,24a |
09
Origami Box with Lid
Eine Anleitung findet man unter 09
Youtube (URL unten)
Es gelingt nicht, den Würfel
ohne Hilfe zu schließen. Der offene Würfel ist stabil.
... ... ...
...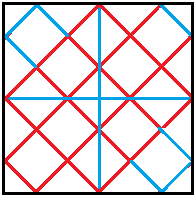 |
Geht man vom fertigen Würfel zurück auf das
Quadrat, ergibt sich das Bild links.
a = 3sqrt(2)x oder näherungsweise x = 0,24a |
10
Fancy Origami Cube
... |
Eine Anleitung findet man unter "10
Youtube" (URL unten).
a = 4x oder x = 0,25a |
Das Besondere ist, dass man
mit wenigen Faltungen einen oben offenen Würfel bilden kann.
...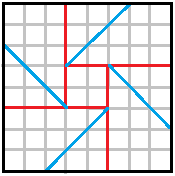
......a = 4x oder x = 0,25a |
 |
11 Origami
Cubic Dice
Eine Anleitung findet man unter 11
Youtube (URL unten)
... ... ... |
 |
... |
Verglichen mit den bisher vorgestellten Würfeln
ist dieser der kleinste.
a = 4*sqrt(2) x oder gerundet x=0.17a. |
Origami-Würfel
aus mehreren Quadraten top
12 Würfel aus zwei Quadraten
Eine Anleitung findet man unter
"12 Youtube"
(URL
unten).
... ... ... |
Es ist nahe liegend. einen Würfel durch zwei oben
offene Würfel zu erzeugen.
Der eine Würfel wird kopfüber in den anderen
gesteckt.
Dazu muss man dafür sorgen, dass der innere etwas
kleiner ist. |
... ... ... |
In diesem Video wird das Problem eleganter gelöst.
Man faltet zwei gleiche, oben offene Würfel.
Dann werden die Würfel über die Keile zwischen
den Quadraten ineinander geschoben.
Wie das gemacht wird, wird im Video gezeigt. Es ist mit
Geduld zu schaffen. |
13
DIY : Origami 3D Cube
... ... ... |
 ... ... |
Der Würfel entsteht aus sechs U-förmigen Modulen.
Wie die Module zusammen gesteckt werden,
wird z.B. im Video "13 Youtube"
(URL unten) gezeigt. |
14
Würfel aus sechs Sonobe-Modulen
... ... ... |
 ... ... |
Wie die Module zusammen gesteckt werden, wird auf meiner
Seite Sonobe-Stern gezeigt. |
15
Variante des Sonobe-Würfels
Wie die Module gefaltet und zusammen gesteckt werden, wird
auf meiner Seite Körper flechten gezeigt.
Würfel aus Streifen
top
16 Würfel aus drei Streifen
17
Offener Würfel aus sechs Streifen
...
Näheres auf meiner Webseite Körper
flechten
18
Flechtwürfel aus vier Streifen
19
Würfel aus einem Streifen
Origami-Würfel
im Internet top
Englisch
Dr Stephen O'Hanlon (Ring of Origami Art)
Water
Bomb ( .pdf file)
Gerwin Sturm (Origami for everyone)
Waterbomb
01 Youtube "Origami with
Thao Bui"
Origami
Cube - "Magic" Cube (Shuzo Fujimoto)
02 Youtube "JeremyShaferOrigami"
Origami
Seamless Cube
03
Youtube "ORIGAMITO"
Wie
man eine Papierschachtel mit Deckel macht
04 Youtube "ORIGAMI
SEAMLESS CUBE (Jo Nakashima)"
ORIGAMI
SEAMLESS CUBE
05 Youtube
"Origami
Gift Box - (@easyorigamiAndCrafts)"
Origami
Gift Box
06
Origami Gift Box / Ring Box Puzzle - (@Easy Origami)
Origami
Gift Box / Ring Box Puzzle
07 Youtube "Closed Origami
Cube Box Instructions - DIY - Paper Kawaii"
Closed
Origami Cube Box
08 Youtube
"Origami Gift Box with one piece of paper - Mica's Paper Craft C"
Origami
Gift Box
09 Youtube
"Origami Box with Lid How to make Origami box" - ArtsfromHeart
Origami
Box with Lid
10 Youtube "Fancy
Origami Cube Tutorial (Hyo Ahn)"
Fancy
Origami Cube
11 Origami
Cubic Dice
Origami
Cubic Dice
12 Youtube
"Kokko
Garden - Würfel aus zwei Quadraten"
Würfel
aus zwei Quadraten
13 Youtube "Ventuno
Art How to Fold an DIY : Origami 3D Cube"
3D
Cube
Deutsch
Michael Schmitz (Mathegami)
Der
Kolumbus-Würfel
Wikipedia
Wasserbombe
(Spielzeug)
zzzebra
Wasserbombe
Referenzen top
(1) Joachim Schönherr, Wir falten und falzen, Leipzig
1990
(2) Therese Mielhaht: Origami Spaß mit Papierfalten,
Köln 1990
(3) Kunihiko Kasahara: Origami - figürlich und geometrisch,
München 2000
(4) Kunihiko Kasahara: Origami - ohne Grenzen, München
2001
(5) Martin Gardner: Mathematische Hexereien, Berlin/Frankfurt
am Main/Wien 1988 [ISBN 3550065787]
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999, erweitert 2024, Jürgen Köller
top |
 ...
...

 ...
...









 .............
............. .......
.......
 ...
...

 ...
... ...
... ...
...
 ....
.... ..
.. .
. ...
... ...
... ...
... .
. ...
...








 ..
.. ....
....
 ...
... ...
...


 ...
... ...
...




 ...
...

 ...
... ...
... ...
... ...
... ...
... ...
...
 ...
...