|
Was ist ein Tetrawürfel?
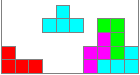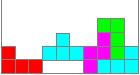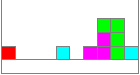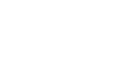
 Die acht abgebildeten Würfelkörper
aus vier Würfeln heißen Tetrawürfel.
Sie sind alle Körper, die man mit vier Würfeln bilden kann. Fünf
der Würfelkörper sind eben, drei sind räumlich.
Die acht abgebildeten Würfelkörper
aus vier Würfeln heißen Tetrawürfel.
Sie sind alle Körper, die man mit vier Würfeln bilden kann. Fünf
der Würfelkörper sind eben, drei sind räumlich.
Die Tetrawürfel heißen
zum Beispiel I, O, L, T, N, Turm rechts, Turm links und Dreibein.
Lässt man die 1x4-Stange und
das 2x2-Quadrat weg und fügt den V-Körper aus drei Steinen hinzu,
so erhält man die sieben Somawürfel.
Quader
aus Tetrawürfeln top
Die Tetrawürfel haben zusammen 32 Würfel. Es
gilt 32=2x4x4.
... ... ... |
... ... ... |
Folglich stellt sich das Problem, aus allen acht Tetrawürfeln
einen Quader 2x4x4 zusammenzusetzen. Es gibt 1390 Möglichkeiten, wie
eine Gruppe von Forschern am MIT mit Hilfe eines Computerprogramms ermittelte
(2). |
Die 1390 Lösungen findet man auf der Webseite von David
J. Goodger (URL unten).
... ... ... |
... ... ... |
Eine andere Zerlegung von 32 ist 32 = 2x2x8. In
der Quaderform 2x2x4 wurden die Tetrawürfel 1967 unter dem Namen "The
Wit's Puzzle" in Hongkong von der Firma Lowe Co. vertrieben (2). |
Der obige 2x2x8-Quader setzt sich aus einem 2x2x4-, einem
2x2x3- und einem 2x2x1-Quader zusammen.
Alle 224 Lösungen findet man auf der Webseite von
David J. Goodger (URL unten).
Weitere Körper aus Tetrawürfeln
top
Interessant wird die Beschäftigung
mit Tetrawürfeln, wenn man sich auf die
Suche nach 32-Würfel-Körpern begibt.
... ... ...
|
 ...... ......
|
Als Beispiel wird die Wanne angeführt, im Entwurf
und gelöst. |
Weitere (lösbare) Entwürfe:
Brunnen, Bett, Penthouse, Turm, Sofa, Würfel und Kreuz, Figur mit
Säule
Skylinetop
Hier veröffentliche ich Ergebnisse von Victor Stok,
die er mir freundlicherweise zur Verfügung gestellt hat. Er hat systematisch
alle Körper aus vier gleichen Schichten untersucht.
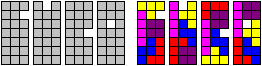
Es gibt 71 Körper, die man in 21 Klassen einteilen
kann. In der folgenden Abbildung steht für jede Klasse ein Körper.
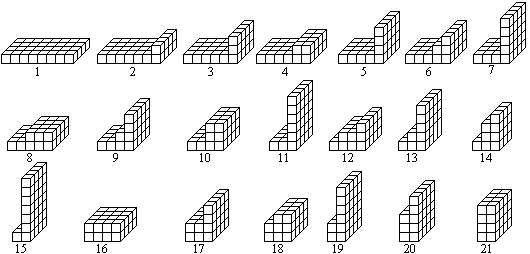 Für die Darstellung der Körper wird unten eine
Notation mit Zahlen gewählt.
Für die Darstellung der Körper wird unten eine
Notation mit Zahlen gewählt.
Der Aufbau der Körper wird durch die Lage der Stangen
und Ihre Höhe festgehalten. So hat zum Beispiel der Körper 12
die Darstellung 1223.
Typ 1: 11111111
Typ 2: 1111112, 1211111, 1121111,
1112111
Typ 3: 111113,
11311, 13111
Typ 4: 111122,
111212, 112112, 121112, 211112, 111221, 112121, 121121, 112211
Typ 5: 11114,
14111, 11411
Typ 6: 11123, 11132, 11213,
11231, 11312, 11321, 12113, 12131, 13112, 21113
Typ 7: 1115,
1511
Typ 8: 11222,
12122, 12212, 12221, 21122, 21212
Typ 9: 1124, 1214,
1241, 1412, 2114
Typ10: 1133,
1313, 3113, 1331
Typ11: 116,
161
Typ12: 1223,
1232, 1322, 2123, 2132, 2231
Typ13: 125,
152,
215
Typ14: 134,
143,
314
Typ15: 17
Typ16: 2222
Typ17: 224,
242
Typ18: 233,
323
Typ19: 26
Typ20: 35
Typ21: 44
Sind die Zahlen grün,
so ist es möglich
den Körper aus
Tetrawürfeln zu legen. Rot steht für
unlösbar
und Schwarz heißt, dass der Körper nicht gelöst, dass aber
die Unlösbarkeit nicht bewiesen wurde.
Daniel Moelle fand mit Computerhilfe
heraus, dass die vier offenen Fälle in Schwarz auch lösbar sind.
Ich konnte die Körper nach seinen Angaben nachbauen.
Vergrößerungsproblem
top
Man kann jeden Tetrawürfel mit allen acht Tetrawürfeln
in doppelter Größe nachbauen.
... |
 |
Die Tetrawürfel I und O sind Quader und wurden schon
oben dargestellt. |
...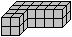 ... ... |
... ... ... |
Tetrawürfel L... |
...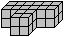 ... ... |
... ... ... |
Tetrawürfel T |
(Lösung von Victor Stok)
...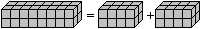 ... ... |
Man kann aus den Tetrawürfeln
zwei Biwürfel bauen. Aus diesen Biwürfeln legt man die Steine
Turm rechts und Turm links, übrigens auch Stein L. |
(Lösung von Darian Jenkins)
Ishino Keiichiro
fand alle Lösungen des Vergrößerungsproblems.
I:224, O:1390,
L:1804, T:356, N:770, Left & Right Towers
both:803, Tripod:126.
(Mitteilung von Darian Jenkins)
Körper
aus gleichen Tetrawürfeln top
Es werden Tetrawürfel von nur einer Sorte vorgegeben.
Aus ihnen können z.B. Würfel gebaut werden.
4x4x4-Würfel:
... |
Man kann aus vier Stücken eine quadratische Platte
bauen. |
Vier Platten dieser Art bilden einen 4x4x4-Würfel.
6x6x6-Würfel:
... ... ... |
9 T-Tetrawürfel bilden eine 6*6-Matte mit 3 Tälern
und 3 Bergen. |
...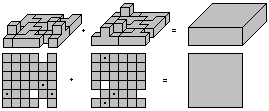 ... ... |
Die gleiche Matte wird noch einmal gebaut, um 90°
gedreht und über die erste gestülpt. Es entsteht ein 2*6*6-Quader
aus 18 Tetrawürfel. |
Drei Platten dieser Art bilden einen 6x6x6-Würfel.

|
Meine 54 handgemachten Tetrominos für den 6x6x6-Würfel.
(Danke Julia) |
4x4x4-Würfel
top
... ... ... |
Ein Satz Tetrawürfel besteht aus 32 kleinen Würfeln. |
... ... ... |
Mit einem zweiten Satz kommt man auf 64 Würfel. |
Das führt zum Problem, mit den
64 Würfeln einen großen 4x4x4-Würfel zu bauen.
Lösung, zugesandt von Darian
Jenkins
... |
 |
Die Paare aus den Tetrawürfeln L, T, N und I führen
zum halben 4x4x4-Würfel. |
... |
...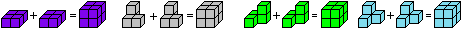 ... ... |
Die dreidimesionalen Tetrawürfel und O legt man
paarweise aufeinander und erhält vier 2x2x2-Würfel oder einen
halben 4x4x4-Würfel. |
Die beiden Hälften bilden den
4x4x4-Würfel.
Tetrominos top
... ... ...
|
Statt der vier Würfel kann man auch vier Quadrate
betrachten.
Dann erhält man statt der acht Tetrawürfel
nur fünf Tetrominos. |
...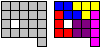 .... .... |
Die fünf Tetrominos haben zusammen 20 Quadrate.
Es ist aber nicht möglich, aus ihnen ein 4x5-Rechteck zu bauen. Man
kann aber ein Quadrat überstehen lassen und nimmt dafür ein Loch
in Kauf. |
... ... ... |
... ... ... |
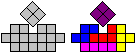
Herbert Fink hatte die Idee, ein 4x6-Rechteck mit 4 Löchern
und ein 5x5-Quadrat mit 5 Löchern aus den fünf Tetrominos zu
legen. |
... ... ... |
Als Puzzle sind die Tetrominos nicht ergiebig.
Die Anzahl der Steine ist zu klein, und die beiden Steine
1x4 und 2x2 sind sperrig. |
... |
Eine Reihe von 3x7-Rechtecken mit einem Loch sind möglich. |
... ... ... |
Mit zwei Sätzen der Tetrominos kann man ein Rechteck
8x5 legen.
Dieses Puzzle wurde als "Adult Game" ;-) in den 1970er
Jahren in der Reihe "Beat the Computer" verkauft.
Laut Beizettel hat der Computer FACOM 270-20 insgesamt
783 Lösungen gefunden.
(Tenyo Co.,Ltd., Tokyo, Japan) |
Tipp von Torsten Sillke
Tetris top
Wenn man die Tetrominos sieht, denkt man an das Computerspiel
Tetris.
...
 ... ...
|
Das Spiel geht so:
Tetrominos fallen in einen Kasten. Man muss durch seitliches
Verschieben und Drehen während das Falles die Steine so bewegen, dass
unten eine waagerechte Schicht mit Quadraten ausgefüllt wird. Das
ist im nebenstehenden Bild gelungen. Der hellblaue Stein fällt im
nächsten Moment in eine Lücke. Man erhält dann Punkte. Die
Reihe aus 10 Quadraten verschwindet. Der nächste RND-Stein folgt von
oben.
Gelingt es nicht eine waagerechte Reihe zu bilden, so
bildet sich ein Haufen. Haben die Steine den oberen Rand erreicht, ist
das Spiel beendet. Das Ende ist unvermeidbar: Die Steine fallen mit zunehmender
Punktezahl immer schneller, schließlich so schnell, dass man nur
noch tatenlos zusehen kann. |
Tetris hat eine interessante Entstehungsgeschichte. Es
wurde 1984 vom Russen Alexij Patschitnow erfunden, der damals im Computerzentrum
der Moskauer Akademie der Wissenschaften tätig war. Es wurde schnell
das Kultspiel Moskauer Studenten.
Auch in Deutschland kursierten vor allem an den Universitäten
bald Versionen, die auf Computern liefen, obwohl diese nicht grafikfähig
waren. Es fielen Steine, die aus dem Doppelkreuz # gebildet wurden.
Minoru Arakawa, Präsident von Nintendo of America,
sah das Spiel auf einer Computermesse und kaufte die Vermarktungsrechte
- günstig (Hinter diesem Wort steht eine eigene Geschichte). Als dann
der Game-Boy auf den Markt kam, wurde er standardmäßig mit diesem
Spiel ausgerüstet. Dadurch wurde das Spiel erst richtig bekannt.
Es gab in den letzten 20 Jahren zahlreiche Versionen dieses
Computerspiels für den PC. Das Shareware-Spiel Wintris ist
wohl das bekannteste. Das Spiel wird mit Taste 5 und den Cursor-Tasten
gesteuert.
Ich empfehle zwei Tetris-ähnliche Spiele: Das Freeware-Spiel
Columns
und das Postcard-ware-Programm ;-) Clickomania. Beide Spiele kann
man aus dem Internet herunterladen. Vorsicht, man kann süchtig werden.
Basteln
von Tetrawürfeln top
Will man sich mit Tetrawürfeln
beschäftigen, muss man sie unbedingt bauen.
Am einfachsten zersägt man
eine quadratische Holzstange, die man in jedem Baumarkt erhält, zu
Würfeln und leimt die Würfel entsprechend zusammen.
Eine weitere Methode ist das Zusammenkleben
von Spielwürfeln. Man verwendet am besten Zweikomponentenkleber, da
dieser nicht sofort erhärtet. So kann man im frischen Zustand die
Würfelkörper zusammensetzen und die Einzelwürfel entsprechend
ausrichten.
Ein billige, mühselige, aber
auch reizvolle Methode ist die Herstellung aus Papier. Man muß dazu
zu jedem Tetrawürfel ein Netz entwerfen,
dann den Körper falten und zusammenkleben.
Tetrawürfel
im Internet top
Deutsch
Andrew Clarke
Polykuben
Wikipedia
Tetris
Englisch
Andrew Clarke
Polycubes
David J. Goodger
Polycubes
Puzzles & Solutions
Eric W. Weisstein (MathWorld)
Polycube
Torsten Sillke
Quader
aus kongruenten Tetrawürfeln
Wikipedia
Tetromino,
Tetris
Japanisch
Square
Cube Puzzle
Referenzen top
(1) Martin Gardner: Mathematical Puzzles & Diversions,
New York 1959
(2) Martin Gardner: Bacons Geheimnis, Frankfurt am Main,
1986 (ISBN 3-8105-0800-4)
(3) R.Thiele, K.Haase: Der verzauberte Raum, Leipzig,
1991 (ISBN 3-332-00480-8)
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |


 ...
... ...
... ...
...

 ...
...
 ...
... ...
...