|
Was ist Happy Cube?
... ... ... |
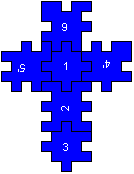
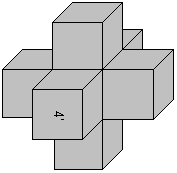
Das Puzzle-Spiel Happy Cube besteht aus 6 Matten aus
dickem, weichem Schaumstoff mit den Farben blau, grün, gelb, orange,
rot und violett. Hier ist die blaue Matte dargestellt.
Jede Matte enthält, von einem Rahmen umgeben, sechs
Stücke in der Form von 5x5-Quadraten. An den Rändern fehlen,
unregelmäßig verteilt, kleine Quadrate.
Es ist möglich, aus sechs Stücken einen 5x5x5-Würfel
zusammenzusetzen.
|
... ... ... |
Je nach Farbe ist der Anspruch der Lösung unterschiedlich.
Die blaue Matte stellt den geringsten Schwierigkeitsgrad dar, die violette
den größten.
Happy Cube wurde im Jahre 1986 von Dirk Laureyssens erfunden.
In Deutschland hieß Happy Cube lange Cube-it. Es führt noch
Namen wie the I.Q.ube, de Wirrel Warrel Kubus, CocoCrash.
Dirk Laureyssens Varianten dieses Puzzles sind
the Little Genius, the Profi Cube, the Marble Cube
(Die Stücke sind austauschbar mit Happy Cube)
Ferner gibt es noch the Planet Cube, Snafu, Snuzzle,
Crico. |
Festhalten einer
Lösung
top
... ..
4'/5'16/2/3. ..
4'/5'16/2/3.
|
Man kann die Stücke auf der Vorderseite einer Matte
von 1 bis 6 durchnummerieren. Die Vorderseite erkennt man an einem kleinen
Kreis mit M in einer Ecke der Matte (blau: oben links). Die Rückseite
von 1 nennt man 1', entsprechend führt man 2' bis 6' ein. Hat man
eine Lösung gefunden, breitet man das Netz des Würfels aus und
achtet darauf, dass das Stück Nr.1 aufrecht in der Mitte steht. Dann
ist die Darstellung einer Lösung eindeutig.
Auch die Matten in den übrigen Farben nummeriert
man so, dass der kleine Kreis links oben oder links unten liegt. Mit den
Zahlen 1 bis 6 und 1' bis 6' kann man die Lösung darstellen. |
Körper (Würfel weiter
unten) top
Mit Hilfe mehrerer Matten ist es möglich, Körper
aus mehreren Würfeln zu bauen. Es folgt eine kleine Auswahl.
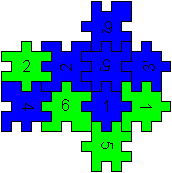
Quader 1x1x2
... ... ...
|
Mit Hilfe der blauen und der grünen Matte kann man
einen Zweiwürfelkörper bauen.
Von den 12 Stücken verwendet man 10.
2 Stücke bleiben übrig. |
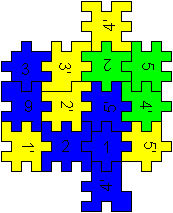
Quader 1x1x3
... ... ...
|
Mit Hilfe der blauen, grünen und gelben Matte kann
man einen Dreiwürfelkörper bauen.
Von den 18 Stücken verwendet man 14.
4 Stücke bleiben übrig. |
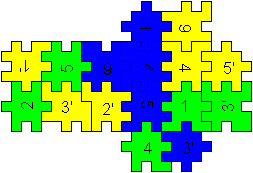
Quader 2x1x2
... ... ...
|
Mit Hilfe der blauen, grünen und gelben Matte kann
man einen Vierwürfelkörper bauen.
Von den 18 Stücken verwendet man 16.
2 Stücke bleiben übrig. |
Maxi-Würfel
2x2x2
... ... ...
|
Aus den 6 Matten mit insgesamt 36 Stücken kann man
mit Hilfe von 24 Stücken einen Maxiwürfel bauen. 12 bleiben übrig.
Theoretisch müsste man mit 5 auskommen.
Stellt man nur 4 Matten bereit, so kommt man auch auf
24 Stücke. Man kann aber zeigen, dass für einen Maxicube 26 Eckwürfelchen
benötigt werden, dass aber die 4 Matten zusammen nur 6*4=24 Eckwürfelchen
haben.
So ist es nicht möglich einen Maxi-Würfel aus
4 Matten zu bauen. |
Maxi-Würfel
2x2x2
... ... ...
|
Es gibt sogar eine Lösung, bei der jede Seitenfläche
einfarbig ist.
(Jan Verbakel, Eindhoven, 1, Seite 15) |
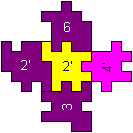
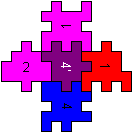
3D-Kreuz
... ... ... |
Will man den Körper links bauen, muss man zuerst
einzeln vier oben offene Würfel aus je fünf Stücken zusammensetzen.
Das mittlere Stück ist jeweils innen unten. (Man behält
die Orientierung im Raum bei.) Dann bildet man einen Kranz aus den offenen
Würfeln. Schließlich bildet man aus den Stücken ganz rechts
zwei offene Würfel, die man oben und unten ansetzt. |
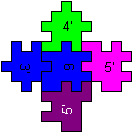
links
|
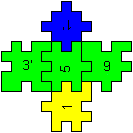
hinten
vorne
|
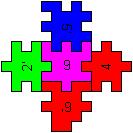
rechts
|
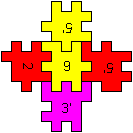
oben
unten
|
Man benötigt 30 von insgesamt 36 Stücken, 6 Stücke
bleiben übrig.
1x2x3-Kasten
mit Kragen
Es ist eine nette Idee, auch den Rahmen mit einzubeziehen.
Hier ist eine Lösung von Jan Verbakel (1, Seite 21):
Rechtecke top
Jean-Marc Dubrunfaut war auf der Suche nach einem Rechteck
aus allen 36 Matten, um ein Laserschneidgerät zu benutzen.
.. .... .... |
Er fand ein 18x2-Rechteck. |
Es gilt 36= 36x1 = 18x2 = 12x3 = 9x4 =6x6,
und
so gibt es vielleicht fünf Rechtecke.
Etwas Mathematik top
Jedes Stück hat 4 Ränder. Dreht man ein Stück
um, so kommen noch 4 Ränder dazu. Die Struktur eines Randes hält
man am besten durch eine Folge von 0 und 1 fest, also durch eine fünfstellige
Dualzahl. Ist ein kleines Quadrat vorhanden, setzt man eine 1, fehlt es,
setzt man eine 0. Anhand des blauen Stücks Nummer 4 wird dieses Vorgehen
veranschaulicht. Die Dualzahl bezieht sich jeweils auf die Kante über
der Dualzahl.

|
Auf diese Weise kann man die Anzahl der 6x6x4x2 = 288 Kantenstrukturen
für alle 6 Matten in einer Tabelle festhalten.
dezimal
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Anzahl der Muster |
dual
00000
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
10001
10010
10011
10100
10101
10110
10111
11000
11001
11010
11011
11100
11101
11110
11111
. |
blau
-
-
-
-
16
2
-
-
-
-
10
4
-
-
-
-
-
-
-
-
2
4
-
-
-
-
4
6
-
-
-
-
8 |
grün
-
-
-
-
14
4
-
-
-
-
10
4
-
-
-
-
-
-
-
-
4
2
-
-
-
-
4
6
-
-
-
-
8 |
gelb
-
-
-
1
8
6
-
1
-
-
12
4
-
-
-
-
-
-
-
-
6
2
-
-
1
-
4
2
1
-
-
-
12 |
orange
-
-
1
1
10
1
3
-
1
1
6
5
3
-
-
-
-
-
1
-
1
6
-
-
1
-
5
2
-
-
-
-
16 |
rot
-
-
1
1
10
3
2
-
1
-
8
3
2
1
-
-
-
-
-
1
3
2
1
-
1
1
3
4
-
-
-
-
18 |
violett
-
-
2
3
6
4
1
3
2
-
6
3
1
1
-
-
-
-
-
-
4
-
1
-
3
-
3
2
3
-
-
-
17 |
Summe
-
-
4
6
64
20
6
4
4
1
52
23
6
2
-
-
-
-
1
1
20
16
2
-
6
1
23
22
4
-
-
-
. |
Man sieht:
> Von den 32 Möglichkeiten, einen Rand zu bilden,
werden nur 22 genutzt (schwarze Zahlen).
> Alle Stücke mit x000x oder x111x werden gemieden
(rote Zahlen).
> Die 4 Paare (00100,11011), (00101,11010), (01010,10101)
und (01011,10100), die zusammen passen, kommen besonders häufig und
bei (fast) allen Farben vor (240 von 288). Bei Blau und Grün werden
nur diese Paare verwendet (fett gedruckt).
> Bei Blau und Grün kommen Strukturen wie x11xx,
xx11x, x00xx oder xx00x nicht vor.
> Zwei Paare sind gleich, nämlich Rot4/Blau3 und
Orange4/Violett4.
Symmetrien top
Durch die Symmetrie eines Randes oder die eines Stückes
wird das Würfel-Suchen leichter.
.
Symmetrische Kanten:
Symmetrische Stücke mit zwei Achsen
Symmetrische Stücke mit einer Achse |
blau
36
2
1 |
grün
32
1
2 |
gelb
24
0
0 |
orange
24
0
2 |
rot
24
0
1 |
violett
14
0
0 |
Dieses sind Ergebnisse von
Schülern, zusammengetragen in einer Projektwoche.
Würfel top
Das Hauptproblem ist das Zusammenbauen eines einfarbigen
Würfels. Durch reines Probieren haben Schüler alle Lösungen
gefunden.
|
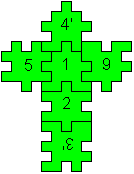
Eine von drei Lösungen

4'/5'16/2/3
|
Eine von fünf Lösungen
4'/516/2/3'
|
Eine von fünf Lösungen
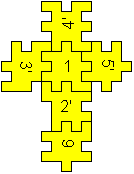
4'/3'15'/2'/6
|
|
Einzige Lösung
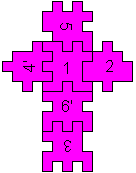
5/4'12/6'/3
|
Einzige Lösung
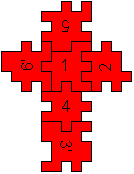
5/6'12/4/3'
|
Einzige Lösung
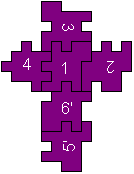
3/412/6'/5'
|
Der blaue und der grüne Würfel sind leicht zu bauen.
Der blaue Würfel ist ein wenig schwerer zu finden, da bei jeder Lösung
die Stücke 1, 2 und 3 in gleicher Anordnung gesetzt werden müssen.
Ich würde dem gelben Würfel den kleinsten Schwierigkeitsgrad
geben, denn bei ihm ist eine elegante Lösung möglich: Die
Kanten 00011 (Stück 2) und 11100 (Stück 3) passen eindeutig zusammen,
dazu ergänzt 1' die beiden Stücke zu einem halben Würfel.
Von da aus ist es nicht weit zum fertigen Würfel.
Der violette Würfel ist wirklich schwer zu lösen,
zumal es vermehrt Irrwege gibt.
Alle Lösungen:
blau, 3 Lösungen: 4'/5'16/2/3,
2/4'15/6'/3', 4'/612/5'/3
grün, 5 Lösungen: 4'516/2/3',
6/213/4/5, 2/6'13/4/5, 3/415/6'/2, 3'514'/2/6'
gelb, 4 (5) Lösungen: 4'/3'15'/2'/6,
6/3'15/2'4', (6/3'15'/2'4',) 6/4'12'/5'/3', 4'/612'/5/3'
orange, 1 Lösung: 5/4'12/6'/3
rot, 1 Lösung: 5/6'12/4/3'
violett, 1 Lösung: 3/412/6'/5'
...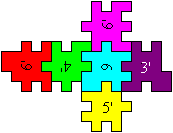 ... ...
|
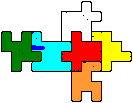
Man kann auch aus sechs Stücken mit verschieden
Farben einen Würfel bauen (links).
In (1, Seite 11) gibt es Computer Ergebnisse über
den Baus eines Miniwürfels mit verschiedenen Farben: 19 Miniwürfel
mit der Verteilung 3+3 (2 Farben), 88 mit 2+2+2 (3 Farben), 21 mit 1+1+1+1+1+1
(6 Farben). |
... ... ... |
Benjamin Koch fand mit Computerhilfe nicht 21, sondern
41 sechsfarbige Lösungen. |
Snafooz top
Snafooz ist eine amerikanische Kopie und steht in Konkurrenz
zu Happy Cube.
... ... ...
|
Snafooz ist in den USA verbreitet.
Ein Satz besteht auch aus sechs Matten. Im Unterschied
zu Happy Cube liegt einer Würfelfläche nicht ein 5x5-Quadrat,
sondern ein 6x6-Quadrat zugrunde.
(Zeichnung von Xandur aus den USA)
|
Rubber top
... ... ... |
Aus Japan stammt ein Puzzle, das
ein 4x4-Quadrat verwendet. Die sechs Stücke, die einen Würfel
bilden, sollen Tiere darstellen. Das ergibt sich aus der Form und der Bemalung.
Das Material kennen wir vom Radiergummi her. Das sollen die Stücke
wohl auch sein. |
Nach (1) steht auf der Plastik-Box:
SEED, PLASTIC ERASER, MADE IN JAPAN. Mein Exemplar hat nur japanische Schriftzeichen.
Referenzen top
(1) Jan de Geus, Joop van der Vaart: Happy Cubes (Wirrel
Warrel), Cubism For Fun (CFF), published by the Nederlandske Kubus Club
(NKS), Heft 50/4 (1999)
Happy Cube im
Internet top
Deutsch
Reich der Spiele
Happy
Cube, Schalenwuerfel
Wikipedia
Happy
Cube
Englisch
Dirk Laureyssens
The
homepage of the inventor of Happy Cube
Happy Cube
SourceForge
Happy Cube
Solver
Snafooz (The
American copy of Happy Cube), Snafooz
Solutions
Thomer Gil
Happy Cube (Wirrel
Warrel) Solver
Wikipedia
Happy
Cube
Spanisch
NN
Evalandia.Soluciones
Cococrash
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |