Was ist ein Spielwürfel?
...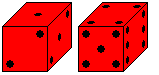 |
Ein Spielwürfel trägt 21 Punkte oder Augen.
Mit ihnen werden auf den Seitenflächen die Zahlen von 1 bis 6 gebildet.
- Man würfelt aus der Hand oder mit einem Lederbecher. Man stülpt
den Lederbecher um oder lässt den Würfel ausrollen. |
Welche der Zahlen 1 bis 6 erscheint, ist dem Zufall überlassen.
Darin liegt der Reiz des Würfelns.
Der Würfel wird bei vielen Brettspielen verwendet.
Er bestimmt oft den Spielverlauf. Er gibt einem Spiel unerwartete Wendungen,
die es beleben.
Es
gibt 30 Spielwürfel
top
... ... ... |
Gibt man die Zahlen 1, 2, 3, 4, 5 und 6 vor und bildet
alle Umstellungen (Permutationen) der sechs Zahlen, so kommt man auf 1*2*3*4*5*6=6!=720
Würfel. Jetzt sind aber auch die Würfel aufgeführt, die
sich durch Drehungen um eine der 13 Achsen ineinander überführen
lassen. Es gibt 24 Drehungen dieser Art. Also gibt es nur 720:24 =30 verschiedene
Würfel. |
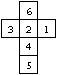
Das folgende Bild erläutert diesen Sachverhalt. (Die
Zahlen unter den Figuren geben die Anzahl der Drehungen an.)

Aussehen
des Standardwürfels top
Es gibt 30 Würfel. Jeder Würfel hat einen Spiegelwürfel,
bei dem die Zahlen rechts und links der Eins ausgetauscht sind.
... ... ... |
Die Würfel können durch eine sechsstellige
Zahl gekennzeichnet werden: Man beginnt mit 1, geht nach oben, dann entgegen
dem Uhrzeigersinn um die 1 herum und hängt noch die Gegenzahl der
1 an. - Der rote Würfel hat z.B. die Darstellung 123546. Die Würfel
links sind nach der Größe dieser Zahlen geordnet. |
Man findet mehr über die Anzahl 30 auf meiner Webseite
Macmahons
Farbwürfel.
In der westlichen Welt ist nur der rote Spielwürfel
üblich.
...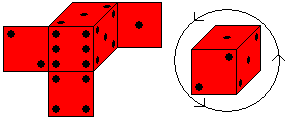 ... ... |
Dieser Spielwürfel hat zwei Eigenschaften:
>Die Augenzahlen gegenüberliegender Flächen
ergänzen sich auf 7.
>Schaut man auf eine Würfelecke mit den Zahlen 1,
2 und 3, so sind diese entgegen dem Uhrzeigersinn angeordnet. |
Die meisten Würfelhersteller halten sich an diese Regeln.
...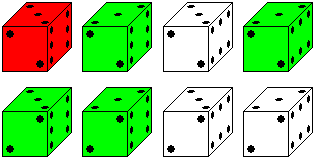 ... ... |
Trotzdem können Würfel immer noch unterschiedlich
aussehen.
Für die Zahlen 2, 3 und 6 gibt es je zwei Ausrichtungen
der Augen, die durch Drehung um 180° ineinander übergehen. Das
führt zu acht Bildern.
Am häufigsten kommt wohl der rote Würfel oben
links vor, aber auch die grünen konnte ich unter meinen 20 Würfeln
entdecken. |
Es folgen vier Puzzles zu den Spielwürfeln.
Summe erraten top
...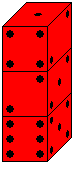 ... ... |
Man baut einen Turm aus mehreren Würfeln.
Ist es möglich, die Summe der Augen der nicht sichtbaren
horizontalen Würfelflächen zu finden?
In diesem Falle besteht der Turm aus drei Würfel.
Fünf Würfelflächen, nämlich die Unterseite des oberen
Würfels und Ober- und Unterseite der beiden unteren Würfel müssen
erfasst werden. |
Lösung
Man beachtet nur die Zahl 1 oben und zählt die darunter
liegenden Würfel. Der Eins liegt die Sechs gegenüber. Für
jeden Würfel zählt man 7. Die Summe beträgt 6+2x7=20.
Würfel Puzzle top
...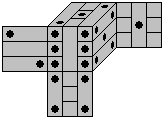 ... ... |
Man erzeugt ein hübsches Würfel-Puzzle, wenn
man den Spielwürfel in neun Balken aufteilt.
 In einer mittleren Schicht legt man die Balken vertikal,
außen jeweils horizontal. Dann ist das Puzzle interessanter.
In einer mittleren Schicht legt man die Balken vertikal,
außen jeweils horizontal. Dann ist das Puzzle interessanter. |
... ... ... |
Man kann den 3x3x3-Würfel auch aus 9 V-Triominos
(Bild) oder aus Somawürfeln bilden und mit entsprechenden Punkten
belegen. |
Rubik's Dice top
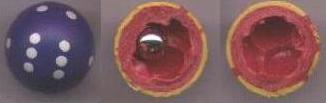
Rubik's Dice ist ein schwarzer Plastikwürfel 7cm x 7cm
x 7cm, der statt Augen kreisförmige Öffnungen nach Art eines
Würfels hat. Im Würfel befinden sich sieben weiße, quadratische
Platten mit roten Kreisen, die innen an die Wände gelegt werden können.
Die direkt an der Öffnung liegende Platte bleibt haften. Man kann
sie von außen mit einem mitgelieferten Stempel wieder lösen.
Die Platten schließen die Öffnungen rot oder weiß. Eine
Lösung des Puzzles ist gefunden, wenn die Platten im Inneren so sortiert
werden, dass der Würfel am Ende nur weiße Augen hat.
Man merkt bald, dass man das Puzzle nicht durch Probieren
lösen kann. Es gibt bei sieben Platten zu viele Möglichkeiten,
die Öffnungen mit den Platten zu schließen. Auch ist das Bewegen
der Platten mühsam.
Man geht so vor: Man kann durch die Löcher in den
Würfel hineinsehen und die Muster beider Plattenseiten abzeichnen.
Die Platten zeigen oben rechts zweistellige Zahlen (Bedeutung?), die als
Namen dienen können. Es ergibt sich das folgende Bild:
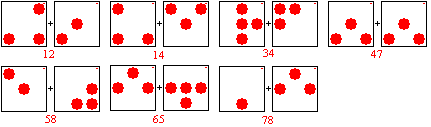
Jetzt ist die Lösung einfach. Wer sich den Spaß
an der Lösung nicht nehmen lassen will, möge jetzt selbst tätig
werden...
Nur Platte 78 (links) passt auf die Sechs, dann nur 65
(links) auf die Fünf, dann nur 34 links auf die Vier, dann nur 58
(rechts) auf die Drei, dann nur 12 (rechts) auf die Zwei und dann nur 14
(links) auf die Eins. Die Platte 47 ist überflüssig.
Es gibt also genau eine Lösung.
Übrigens habe ich inzwischen den Würfel aufgesägt
:-(, um die Seite einer Platte zu scannen. Außerdem war ich neugierig
zu erfahren, warum die Platten haften bleiben. - Die Platten sind aus Eisenblech.
Sie werden von sechs ringförmigen Magneten gehalten. Diese befinden
sich im Inneren in den Mitten. Ihre Umrisse sind von außen zu erkennen.
Summenproblem top
...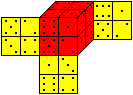 ... ... |
Gegeben sind 8 Spielwürfel. Man soll einen 2x2x2-Würfel
bauen, so dass die Summe der Augenzahlen auf jeder Seitenfläche gleich
ist.
Es folgt eine von 20 736 Lösungen für die Summe
14. |
Mehr findet man in dem Artikel "Würfelspiele im
Intercity" von Reinhard Droste in <bild der wissenschaft> 3-1980.
Weitere Würfelformen
top
Der Würfel gehört zu den fünf platonischen
Körpern. Das sind die Körper, die nur von regelmäßigen
Vielecken gebildet werden. Sie heißen Tetraeder, Hexaeder (Würfel),
Oktaeder, Ikosaeder und Pentagondodekaeder.
Man kann nach ihrem Vorbild Würfel bauen.
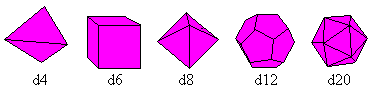

Mit ihnen kann man 4,6, 8,12 oder 20 Zahlen würfeln.
Es zählt immer die Zahl, die oben liegt. Eine Ausnahme bildet das
Tetraeder. Da zählt die Zahl, die verdeckt ist, oder besser die, die
wie im Bild an der Spitze steht.
Im Internet habe ich weitere interessante Würfelkörper
gefunden, die mathematisch möglich sind. Sie sind konvex, werden von
kongruenten Vielecken gebildet und jedes Vieleck ist bezüglich des
Schwerpunktes gleichberechtigt ("Properties of Dice", URL unten).
Es gibt zahlreiche andere Würfelformen. Noch zwei
werden herausgegriffen.
... ... ... |
Interessant ist der Würfel d10. Er hat angenähert
die Form einer Doppelpyramide, wobei die gemeinsame Grundfläche in
etwa ein Fünfeck ist. Er trägt die Zahlen 0 bis 9, also die Ziffern
des Zehnersystems. Auf diese Weise kann man mit mehreren Würfeln dieser
Art mehrstellige Zufallszahlen finden. |
.... ... ... |
Der Würfel in Kugelform ist originell:
Im Inneren befindet sich eine Stahlkugel, die nur in eine
der sechs Mulden zur Ruhe kommen kann.
So erscheinen trotz der Kugelform die Augen 1 bis 6 immer
oben. |
...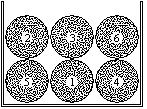 ... ... |
Es gibt viele Möglichkeiten zufällige Zahlen
zu ermitteln. Nach dem Vorbild der Lottoziehung könnte man 6 gleiche
Kugeln (TT-Bälle!) mit Zahlen versehen, in einen Behälter ("Urne")
legen, gut mischen und dann eine Kugel verdeckt ziehen. Die gezogene Kugel
trägt die "gewürfelte" Zahl. |
Neues Würfeln bedeutet, die gezogene Kugel vor jedem
"Würfeln" wieder zurückzulegen und dann erst wieder zu ziehen.
Dieses ist das übliche Modell in der Mathematik
den Würfel zu simulieren und in eine Theorie einzubinden.
Trotz der Inflation von Würfelformen:
Der normale d6 ist und bleibt wohl der Standardwürfel.
Er hat etliche Vorteile:
>Die Zahl 6 ist nicht zu groß und nicht zu klein.
Mit 6 Zufallszahlen kann man gut spielen.
>Der normale Würfel rollt am besten, vor allem wenn
die Ecken abgerundet werden. Das ist bei normalen Würfeln üblich.
>Er ist leicht präzise herzustellen, da die Würfelflächen
aufeinander senkrecht stehen.
Gefälschte Würfel
top
Man nennt einen Würfel, der beim Würfeln bestimmte
Augen häufiger anzeigt als andere, einen gefälschten oder gezinkten
Würfel.
Man kann den normalen Würfel auf unterschiedliche
Weise manipulieren:
> Ein Würfel trägt nicht sechs verschiedene
Zahlen. Bis zu drei Zahlen können fehlen, da man immer nur drei Seiten
des Würfels sieht.
> Man kann einen Würfel in der äußeren
Form kaum merklich verändern. Die Ecken können unterschiedlich
stark gerundet werden, die Seitenquadrate unterschiedlich groß sein.
> Ein Würfel kann im Inneren manipuliert sein. Befindet
sich im Inneren unsymmetrisch ein Metallkörper, so wird sich der Würfel
bevorzugt so bewegen, dass der schwerere Körper unten liegt. - Ein
Hohlraum wird meist oben sein.
> Eine Quadratfläche eines Würfels kann so
behandelt werden, dass der Würfel beim Ausrollen auf ihr bevorzugt
liegen bleibt.
> Man kann zum Manipulieren magnetische Kräfte einsetzen,
die sogar durch Funkkontakt eingeschaltet werden können.
Die Grenzen zwischen einem fairen und einem gefälschten
Würfel sind fließend. Zur Entscheidung führt man heute
den Chi-Quadrat-Test durch, bei dem typische Abweichungen von der Gleichverteilung
erfasst und bewertet werden.
Der Computer würfelt
top
Man kann das Würfeln mit dem
Computer simulieren. Dazu gibt es in allen Programmiersprachen (z.B. in
Visual Basic) einen Zufallsgenerator, der Dezimalzahlen zwischen 0 und
1 liefert (A=RND).
...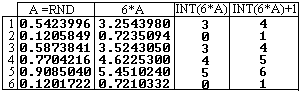 ... ... |
Man multipliziert diese Zahlen mit 6, schneidet mit der
Funktion INT die Dezimalen ab und addiert 1.
Das wird links an sechs Beispielen demonstriert.
Man erhält hier zufällig die Zahlen 4, 1, 4,
5 ,6 und 1. |
Es macht keine große Mühe so mal eben 6000x
zu "würfeln".
...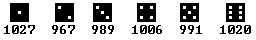 ... ... |
Die Häufigkeitstabelle zeigt, dass die Zahlen von
1 bis 6 etwa gleich oft vorkommen, nämlich etwa 1000x. |
Das sagt auch die Wahrscheinlichkeitstheorie. Die Wahrscheinlichkeit,
eine Zahl (z.B. eine Drei) zu würfeln, ist gleich 1/6 (=1000:6000).
Nach dem Gesetz der großen Zahl wird 1/6 immer besser erfüllt,
je größer die Anzahl der Würfe ist. - Andererseits muss
ein guter Würfelsimulator eine gewisse Streuung haben. Darin liegt
gerade die Schwierigkeit, einen guten Zufallsgenerator zu programmieren.
Für das praktische Würfeln ist eine Wahrscheinlichkeitsaussage
wie 1/6 wenig nützlich. Man weiß nichts über den nächsten
Wurf. Jeder Wurf ist unabhängig vom vorhergehenden Wurf.
Spielwürfel
im Internet
top
Deutsch
Faroul
Würfel
Wikipedia
Spielwürfel
Englisch
Kevin Cook
Collection of
Dice
Eric W. Weisstein (MathWorld)
Dice
Klaus Æ. Mogensen
Properties
of Dice
Leo van der Heijdt
Welcome to
the Homepage of DICE Collector (Dutch / English)
Wikipedia
Dice
Referenzen top
(1) Robert E.Lembke, Michael Schiff: Das große
Haus- und Familienbuch der Spiele, Frankfurt a.M. 1970
(2) Martin Gardner: Mathematische Hexereien, Berlin 1988
(3) Rüdiger Thiele, Konrad Haase: Der verzauberte
Raum, Leipzig 1991
(4) Reiner Knizia: Das große Buch der Würfelspiele
(124 Spiele), München 2000
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |