|
Was ist ein Hexomino?
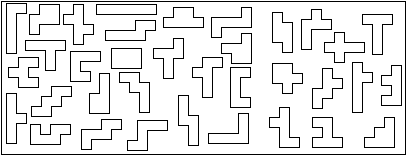
Hexominos heißen Figuren, die man aus sechs Quadraten
bilden kann. - Es gibt 35 verschiedene Figuren.
Umhüllende
Rechtecke top
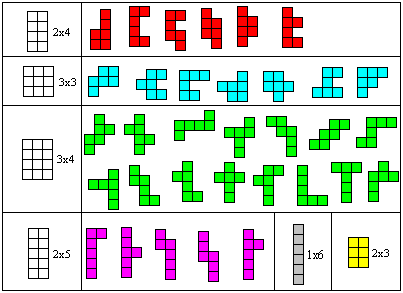
Man kann um ein Hexomino ein möglichst kleines Rechteck
legen (umhüllendes Rechteck). So kommt man zu einer Einteilung in
sechs Gruppen.
Rechteckproblem
top
Es ist möglich, aus allen Figuren mit fünf
Quadraten (Pentominos) verschiedene Rechtecke zu legen.
Das Problem stellt sich auch bei Hexominos. Alle 35 Hexominos
umfassen 35*6=210 Quadrate. Da sind viele Rechtecke möglich.
Lässt sich ein Rechteck 21x10 legen?
Behauptung: Das Rechteckproblem ist unlösbar.
Angenommen, es gibt ein Rechteck
aus allen Hexominos (oben). Dann färbt man die Quadrate des Rechtecks
abwechselnd und erhält 105 weiße und 105 schwarze Quadrate:

Andererseits kann man auch die Hexominos
entsprechend färben:
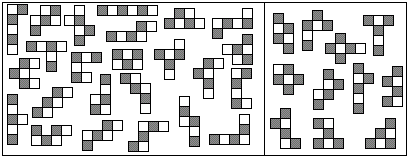 So entstehen 24 "ungerade" Hexominos mit drei schwarzen und
drei weißen Quadraten und 11 "gerade" Hexominos mit vier schwarzen
und zwei weißen Quadraten. Zwei schwarze und vier weiße Quadrate
wären auch möglich.
So entstehen 24 "ungerade" Hexominos mit drei schwarzen und
drei weißen Quadraten und 11 "gerade" Hexominos mit vier schwarzen
und zwei weißen Quadraten. Zwei schwarze und vier weiße Quadrate
wären auch möglich.
Doch in beiden Fällen gelangt man zu einer geraden
Anzahl gefärbter Quadrate: 24*3, 11*4 oder 11*2.
Also ergibt sich ein Widerspruch. 105 ist ungerade. Die
Anzahl aller gefärbten Quadrate in einer Figur ist immer gerade.
Ergebnis: Ein Rechteck 21*10 ist
unmöglich.
Auf die gleiche Weise kann man sich
klar machen, dass es andere Rechtecke wie 14*15 oder 6*35 nicht geben kann.
Übrigens kann man aus Figuren
mit 7 oder mehr Quadraten aus einem anderen Grund kein Rechteck bauen.
Die Figuren können ein Loch haben.
...
|
Links steht das einzige Septomino mit einem Loch. |
Figuren aus Hexominos
top
...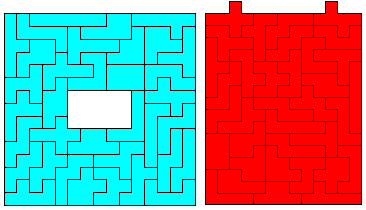 ... ... |
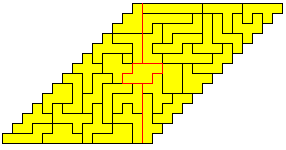
Kompakte Rechtecke aus allen Hexominos
sind nicht möglich.
So gibt es nur Rechtecke mit Löchern
(blau) oder Rechtecke mit einzelnen hervorstehenden Quadraten (rot)
Zwei Beispiele von Andrew
Clarke! |
... ... ... |
Wie bei Pentominos gibt es unzählige
neue Figuren.
Links das Beispiel eines Parallelogramms
aus Gardners Buch (1). |

Figuren
aus gleichen Hexominos top
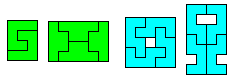 Von Interesse sind Rechtecke, die man aus gleichen Hexominos
bauen kann (grün). Das ist nicht immer möglich.
Von Interesse sind Rechtecke, die man aus gleichen Hexominos
bauen kann (grün). Das ist nicht immer möglich.
Freie Figuren gibt es reichlich (blau).
Besondere Hexominos
top
Symmetrische Hexominos
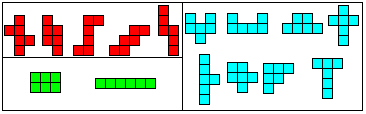 Von den 36 Hexominos sind 15 symmetrisch.
Von den 36 Hexominos sind 15 symmetrisch.
Sie sind punktsymmetrisch, achsensymmetrisch mit einer
Achse oder mit zwei Achsen.
Netze von Würfeln
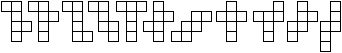 11 Hexominos können als Netz eines Würfels verwendet
werden.
11 Hexominos können als Netz eines Würfels verwendet
werden.
Hexominos mit Rubik's Magic Master Edition top
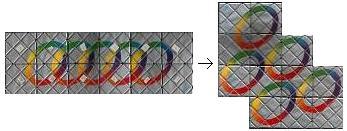 Magic ist ein Klappspiel, bei dem das Hauptproblem darin
besteht, eine Matte von 6x2 Quadraten in eine herzförmige Figur zu
verwandeln. Dabei müssen 5 ineinander verschlungene Ringe in 5 freie
Ringe auf der Rückseite übergehen.
Magic ist ein Klappspiel, bei dem das Hauptproblem darin
besteht, eine Matte von 6x2 Quadraten in eine herzförmige Figur zu
verwandeln. Dabei müssen 5 ineinander verschlungene Ringe in 5 freie
Ringe auf der Rückseite übergehen.
Klappt man die Grundfigur links um die beiden Symmetrieachsen
des Rechtecks, so erhält man die einfachen Hexominos 1x6 und 2x3.
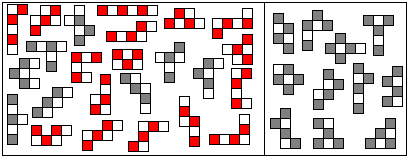
Es gibt kompliziertere Klappfolgen, die zu 16 Hexominos führen. Sie
sind unten rot gekennzeichnet. Es ist bemerkenswert, dass nur ungerade
Pentominos entstehen.
Räumliche Hexominos
top
... ... ...
|
Es gibt 166 Körper aus sechs Würfeln, links
ein Beispiel. |
Hexominos im Internet
top
Deutsch
Andrew Clarkes Poly Seiten
Polyominoes
Richard Mischak (Zahlenjagd)
Würfelpuzzles
Englisch
Andrew Clarke's THE POLY PAGES
Polyominoes
gamepuzzles
Naming
the Hexominoes, Naming
the Hexacube Pieces
Gerard's Home Page
Gerard's
Universal Polyomino Solver
Joseph Myers
Polyomino
tiling
Steven Dutch
Polypolygon
Tilings (archived)
Torsten Sillke
Tiling
and Packing results
Wikipedia
Hexomino
Referenzen
top
(1) Martin Gardner, Mathematical Puzzles & Diversions,
New York 1959 (English)
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |







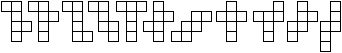


 ...
... ...
...