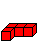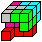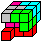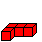
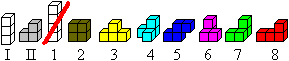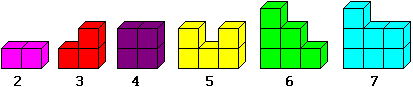Was ist ein Somawürfel?
Die abgebildeten Würfelkörper
heißen Somawürfel. Sie enthalten 1x3 + 6x4 = 27 Einzelwürfel.
Grundproblem top
... ... |
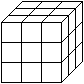Das Grundproblem besteht darin,
die sieben Somawürfel (auch Steine genannt) zu einem 3x3x3-Würfel
zusammenzusetzen.
Die Chancen dieses 3D-Puzzle zu
lösen, sind relativ groß, denn es gibt immerhin 240 Möglichkeiten
des Zusammenfügens, von Symmetrien abgesehen. |
Beim ersten Probieren braucht man bis
zu 15 Minuten dieses Puzzle zu lösen. Man kommt leichter zum
Erfolg, wenn man zuerst die drei dreidimensionalen Somakörper 5,6
und 7 verbaut.
Drei Lösungen
1
... |
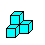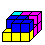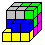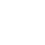Lösung 1 war meine erste Lösung........................................................... |
2
... ... |
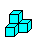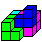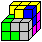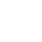Lösung 2 ist leichter zu merken:
Man beginnt mit einem symmetrischen Körper aus den drei dreidimensionalen
Steinen 5, 6 und 7, dann folgt Stein 4. |
3
... |
Lösung 3 zeigt einen der wenigen
Fälle, bei dem Stein 7 keine Ecke bildet. |
Alle 240 Lösungen
Loesung Nr: 1
000 100 000 011 000
000 000
000 000 000 001 110
000 000
000 000 011 000 100
000 000
000 100 000 001 000
010 000
000 110 001 000 000
000 000
000 000 001 000 000
000 110
000 000 000 000 000
111 000
111 000 000 000 000
000 000
100 000 000 000
000 000 011
|
... ... |
Jochen Wermuth stellt mir für diese Homepage alle
240 Lösungen zur Verfügung, ermittelt in einem Programm in C++.
Die Notation links wird verwendet.
Das Schema hat sieben Spalten. In jeder Spalte wird der
ganze Würfel und die Lage eines Somawürfels dargestellt.
Den drei Blöcken in den Zeilen sind die drei Ebenen
oben, Mitte und unten zugeordnet. |
Ich biete mit Einverständnis
des Autors alle
240 Lösungen zum Herunterladen
an, desgleichen den Quelltext in C++.
Lage der
Somawürfel 2 und 3 top
Diese beiden Steine enthalten eine 1x1x3-Stange. Daraus
ergeben sich folgende Aussagen.
Stein 3 bildet entweder 0 oder 2 Ecken.
Stein 2 kann 0, 1 oder 2 Ecken bilden.
Jetzt gibt es zwei Möglichkeiten:
(1) Stein 3 bildet keine Ecke. Die übrigen 6 Steine
liefern maximal 2+5 Ecken. Das ist nicht möglich, da dann nicht 8
Ecken zusammenkommen.
(2) Stein 3 bildet 2 Ecken. Die übrigen 6 Steine
liefern die restlichen 6 Ecken. Das ist möglich. Dann muss aber Stein
2 immer mindestens eine Ecke übernehmen.
Ergebnisse:
........ ..
Stein 3 bildet zwei Ecken.
|
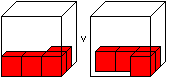
Stein 2 muss immer mindestens eine Ecke bilden,
darf also nicht in der Mitte liegen.
|
Dies können die ersten Schritte sein um nachzuweisen,
dass es 240 Lösungen gibt.
Körper
aus Somawürfeln top
Interessant wird die Beschäftigung
mit Somawürfeln, wenn man sich auf die Suche nach neuen 27-Würfel-Körpern
begibt, zum Beispiel nach einem "Auto".
Weitere bekannte (lösbare) Körper
sind Sofa, Bett, Wanne, Tor, Grab und Turm:
Es gibt unzählige Körper
aus Somawürfeln.
Das zeigen die folgenden Überlegungen zum Entwurf
neuer Körper.
... ... |
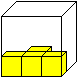
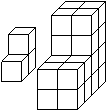
Alle Somawürfel bestehen aus 27 Einzelwürfeln.
Gibt man eine Matte von 5x4=20 Würfeln vor, so gibt es [20 über
7] = 20!/13!/7! = 77520 Plätze für die restlichen 7 Würfel,
also 77520 Würfelkörper. Links wird ein Beispiel angegeben. |
Übrigens ist "6 aus 49" beim Lotto das gleiche mathematische
Problem.
... ... |
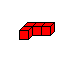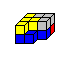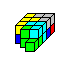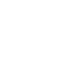
Fordert man eine Stange aus fünf Würfeln, so
können zwei Würfel frei gewählt werden. Das führt zu
[15 über 2] =15!/13!/2! = 105 Würfelkörper. Links ein Beispiel.
Verlangt man noch zusätzlich Symmetrie, so bleibt es bei einer überschaubaren
Zahl von 18 Würfelkörper. Sie werden rechts in der Aufsicht und
unten im Schrägbild dargestellt. |
... ... |
Zwei Würfelkörper sind unlösbar.
Das Vergrößerungsproblem
top
Kann man die Somasteine vergrößert nachlegen?
Bei den Pentominos und Tetrawürfeln ist das Vergrößerungsproblem
ergiebig, bei den Somawürfeln nicht.
Nur der Dreierwürfel kommt in Frage.
Dann braucht man alle übrigen sechs Somawürfel,
um ihn in doppelter Größe nachzubauen.
Basteln
von Somawürfeln top
Will man sich mit Somawürfeln
beschäftigen, muß man die sieben Somawürfel unbedingt bauen.
Am einfachsten zersägt man
eine quadratische Holzstange, die man in jedem Baumarkt erhält, zu
Würfeln und leimt die Würfel entsprechend zusammen.
Eine weitere Methode ist das Zusammenkleben
von Spielwürfeln. Man verwendet am besten Zweikomponentenkleber, da
dieser nicht sofort erhärtet. So kann man im frischen Zustand den
3x3x3-Würfel zusammensetzen und die Einzelwürfel entsprechend
ausrichten.
Ein billige, mühselige, aber
auch reizvolle Methode ist die Herstellung aus Papier. Man muß dazu
zu jedem Somawürfel ein Netz entwerfen, dann die Körper falten
und zusammenkleben.
Ein Tipp für Lehrer:
Wenn in Klasse 6 im Mathematikunterricht
die Raummaße anstehen, baut jeder Schüler zu Hause einen 1dm³-Würfel
aus Pappe, um eine Vorstellung von 1 dm³ zu bekommen. Bei den großen
Klassenstärken heute :-( kommen so 27 brauchbare Würfel
zusammen. Die Würfel leimt man zu Somawürfel zusammen und hat
ein schönes Pausenspiel.
Die Somawürfel kann man kaufen.
1969 vertrieb Parker Brothers die Somawürfel in den
USA. Es ist zu vermuten, dass sie den Namen "Soma cube" schützen ließen..
Heute werden in Deutschland Somawürfel häufig
auf Weihnachtsmärkten angeboten, meist ohne Namen oder unter einem
Namen wie Ostfriesenwürfel ;-). Eine Version heißt Babylon.
Das ist der Rehmsche Spielsatz.
Die Somawürfel werden mit einem Kartenspiel versehen
in den USA mit dem Namen Block by Block vertrieben. Ich kaufte es
in Las Vegas 1996.
Drei Varianten top
1.Variante: Soma schräg
top
Es gibt eine Kuriosität: Statt eines Würfels
als Grundbaustein verwendet man ein Parallelepiped oder Spat. Das ist ein
Körper, der nur von Parallelogrammen begrenzt wird. In diesem Falle
ist das Parallelogramm eine Raute mit einem Innenwinkels von 50°.
Man sollte meinen, dass man eine Lösung des 3x3x3-Würfel-Problems
auf
diese Körper einfach übertragen kann. Das gelingt selten.
... ... |
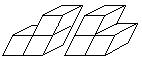Fügt man 3 oder 4 Spate zusammen, so gibt es zu
jeder der sieben Formen zwei Möglichkeiten. Dadurch ist die Anzahl
240 Lösungen drastisch herabgesetzt.
Ich habe nur eine Lösung gefunden. |
(Soma schräg, HOLZINSEL 56290 Beltheim, Art.-Nr.
019/1)
2.Variante:
Schachbrett-Somawürfel
top
Man erzeugt dieses Soma-Puzzle, indem man einen Würfel
(z.B. mit Methode 2, oben) baut und die Einzelwürfel abwechselnd schwarz
und weiß färbt. Diese Färbung nehmen dann die sieben Somawürfel
an.
Aufgabe ist es, aus den Somawürfeln wieder den 3x3x3-Würfel
zusammenzusetzen.
3.Variante: Farbwürfel
top
... ...
|
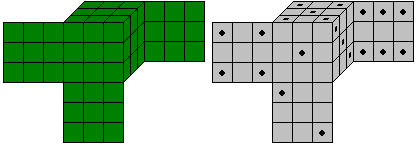Man erzeugt neue Soma-Puzzle, indem man den 3x3x3- Würfel
baut und die Oberfläche mit einer Farbe färbt oder mit einem
Muster (Beispiel: Spielwürfel) versieht. Diese Veränderungen
nehmen dann die sieben Somawürfel an. Zur Verwirrung kann man die
Veränderungen auch auf innen liegende Quadrate entsprechend übertragen. |
Aufgabe ist es dann, aus den Somawürfeln wieder den
3x3x3-Würfel zusammenzusetzen.
Geschichte top
Der Däne Piet Hein wählte 1936 sieben Würfelkörper
so aus, dass er einen 3x3x3-Würfel zusammensetzen konnte. Von allen
Würfelkörpern, die man aus 3 oder 4 Würfeln bilden kann,
wählte er die aus, die keinen Quader bilden:
Er entnahm vielleicht dem Buch "Schöne neue Welt" von
Aldous Huxley den Namen Soma. Soma war eine Droge in einem fiktiven Staat
des Jahres 2600 (3).
Piet Hein (1905-1996) war ein Dichter und Wissenschaftler
mit weit gefächerten Interessen.
J. H. Conway und M.J.T. Guy
fanden 1961 heraus, dass es 240 verschiedene Möglichkeiten gibt einen
3x3x3-Würfel zusammenzusetzen. Computer bestätigten später
dieses Ergebnis.
Berühmt wurde der Somawürfel aber erst durch
Veröffentlichungen des Magazins Scientific American (1958).
In Deutschland verbreitete
Bild der Wissenschaften
das Puzzle (1967).
Ähnliche
Würfelprobleme
top
Tetrawürfel
Theodore Katsani schlug in den 1950ern Jahren ein Spiel
vor, das alle Polykuben aus vier Würfeln umfasst.
Es ist kein Würfel möglich, aber 8*4=32 ermöglicht
die Quader 2x4x4 oder 2x2x8 (4).
Mehr findet man auf meiner Seite Tetrawürfel.
Rehmscher Spielsatz
Es geht um das Problem: Aus welchen Würfelkörpern
mit 3 oder 4 Würfeln kann man einen 3x3x3-Würfel bauen?
|
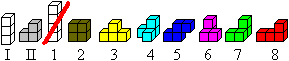
Es gibt 2 Dreierwürfel und 8 Tetrawürfel.
...
Die Bezeichnungen stammen aus Buch 5. |
Dann gibt es theoretisch 14 Möglichkeiten für einen
3x3x3-Würfel, da nur 27=6*4+3 gilt.
I345678 (138)
|
I245678 (000)
|
I235678 (031)
|
I234678 (099)
|
I234578 (245)
|
I234568 (245)
|
I234567 (027)
|
II345678 (240)
Somawürfel
|
II245678 (047)
|
II235678 (261)
|
II234678 (221)
|
II234578 (337)
|
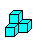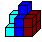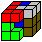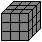
II234568 (337)
|
II234567 (039)
|
Mit Ausnahme der Kombination II245678
(3 fehlt) bilden alle anderen einen Würfel (5).
Die Zahl in Klammern gibt die Anzahl
der Lösungen an (Torsten Sillke, Rehm's 3-Cubes, URL unten).
Hohlwürfel
... ...
|
Aus den Dreierwürfeln I und II und den Tetrawürfeln
3,4,6,7 und 8 kann man einen Hohlwürfel bauen.
Es gilt 2*3+5*4=26 |
Man kann nach Lösungen mit anderen Tetrawürfel
fragen und dann nach der Anzahl der Lösungen. (Die Anregung stammt
von Volker Latussek aus Würzburg.)
Weitere 3x3x3-Puzzles
top
Die Somawürfel bilden zusammen die Würfelsumme
27. Es gilt 27=3+4+4+4+4+4+4.
Man kann sich gut vorstellen, dass es zwischen den trivialen
Zerlegungen 27=1+1+...+1 und 27=9+9+9 weitere Zerlegungen gibt, die auch
zu brauchbaren Puzzles führen.
In diesem Kapitel stelle ich einige Puzzles vor, denen
ich eher zufällig begegnete.
Diabolical
Cube - Dean Hoffmann (27=2+3+4+5+6+7)
... |
Einige (lösbare) symmetrische Körper |
Mikusinski's
Cube (27=4+4+4+5+5+5)
... |
Es gibt nur zwei Lösungen. |
|
... |
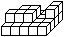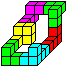
Nach längerem Herumspielen fand ich eine 5x4 Matte
mit 7 aufgesetzten Würfeln. |
Der
vertrackte Würfel- The tricky cube (27=4+4+4+5+5+5),
"Toys pure", Art.-Nr.:HS 630
... |
|
... |
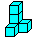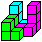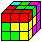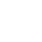
Man kann mit allen sechs Steinen einen geschlossenen
Ring bilden. |
Loops
cube (27=4+4+4+5+5+5), designed and made by René Dawir
... |
Reihenfolge beim Lösen: 564321 |
|
Somawürfel
im Internet top
Deutsch
http://www.zahlenjagd.at/
Würfelpuzzles
Matroid Matheplanet
Der
Soma Würfel
Thimo Rosenkranz
Soma-Figuren
Wikipedia
Somawürfel
Englisch
Christian Eggermont
The
Soma Cube ("Go to the puzzles!")
Ed Vogel
A very large Soma puzzle
at the Minnesota State Fair 2006 |
|
Eric W. Weisstein, (MathWorld)
Soma
Cube
pelikanpuzzles.eu
SHRINKING
SOMA (more at Youtube)
Stewart T. Coffin
The
Puzzling World of Polyhedral Dissections
Thorleif Bungård
Thorleif's
SOMA page
Torsten Sillke
cube-secrets,
Rehm's
3-Cubes (1980)
Wikipedia
Soma
cube, Bedlam cube,
Conway
puzzle
Youtube
SOMA
CUBE puzzle solution, Puzzle
Cube Solution, How
to solve the Bedlam Cube Retro,
SOMA
CUBE ANIMATION (12 figures, 3D puzzle solution)
Referenzen top
(1) "Bild der Wissenschaft" November 1967
(2) Pieter van Delft /Jack Botermans: Denkspiele der
Welt, München 1980 (1998 neu aufgelegt) [ISBN 3-685-1998)
(3) Martin Gardner: Bacons Geheimnis, Frankfurt am Main,
1986 [ISBN 3-8105-0800-4]
Fast 30 Jahre nach Erscheinen einer Kolumne in der
Septemberausgabe 1958 von <Scientific American> zieht der Autor eine
Bilanz der "Somaforschung".
(4) R.Thiele, K.Haase: Der verzauberte Raum, Leipzig,
1991 [ISBN3-332-00480-8]
(5) R.Thiele, K.Haase: Teufelsspiele, Leipzig, 1991 [ISBN
3-332-00116-7]
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |
