|
Was ist die Sinusfunktion?
... ... |
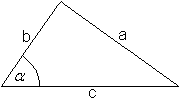Eine Funktion ist eine eindeutige Zuordnung. Bei der
Sinusfunktion wird dem Winkel im rechtwinkligen Dreieck das Verhältnis
der Gegenkathete zur Hypotenuse zugeordnet. Das Verhältnis nennt man
Sinuswert oder kurz Sinus.
In der Formelsprache heißt das [alpha 
sin(alpha) mit sin(alpha)=a/c]. |
Für diese erste Definition ist der Definitionsbereich
D={alpha| 0<alpha<90°}.
Von den sechs Seitenverhältnissen,
die am rechtwinkligen Dreieck abzulesen sind und die zu sechs trigonometrischen
Funktionen führen, geht es auf dieser Webseite im Wesentlichen nur
um den Sinus.
Am Ende werden alle Funktionen vorgestellt.
Sinuswerte
im rechtwinkligen Dreieck top
| ...... |
Da die Kathete a eines rechtwinkligen Dreiecks immer
kleiner als die Hypotenuse c ist, sind die Sinuswerte a/c kleiner als 1. |
Bestimmte Sinuswerte erhält man über
spezielle Dreiecke.
... ... |
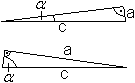Nähert sich in einem rechtwinkligen Dreieck der
Winkel alpha dem Nullwinkel, so geht a/c gegen 0.
Nähert sich der Winkel alpha dem rechten Winkel,
so geht a/c gegen 1.
Deshalb wird sinnvollerweise sin(0°)=0 und sin(90°)=1
definiert. |
Die Berechnungen lassen sich
in einer Wertetabelle zusammenfassen.
| alpha |
0°
|
30°
|
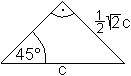
45°
|
60°
|
90°
|
| sin(alpha) |
0
|
1/2
|
(1/2)sqrt(2)
|
(1/2)sqrt(3)
|
1
|
Die fünf Funktionswerte
kann man sich leicht merken. Die Terme sind von der gleichen Form.
| alpha |
0°
|
30°
|
45°
|
60°
|
90°
|
| sin(alpha) |
(1/2)sqrt(0)
|
(1/2)sqrt(1)
|
(1/2)sqrt(2)
|
(1/2)sqrt(3)
|
(1/2)sqrt(4)
|
Wurzelterme (irrationale
Zahlen) als Funktionswerte sind Ausnahmen. Im Allgemeinen sind die Sinuswerte
transzendente Zahlen, die angenähert als Dezimalbrüche angegeben
werden können. Diese werden über konvergente Reihen gewonnen,
dann aber in beliebiger Genauigkeit.
Es ist heute kein Problem, sich gerundete Sinuswerte
über den Taschenrechner zu verschaffen. Man bestimmt z.B. sin(52°)
mit dem TI 30 über die Tastenfolge (5) (2) (SIN). Es ergibt sich sin(52°)=
0,788010754. Es ist allerdings sinnlos, alle 9 Dezimalen vom Rechner zu
übernehmen. Das ist zu genau, denn der Winkel ist nur auf zwei Ziffern
genau vorgegeben. Nach einer Faustregel genügen dann beim Sinuswert
auch zwei geltende Ziffern, sin(52°)= 0,79.
Es ist üblich, den Sinuswert auf vier Dezimalen
genau zu runden. Dazu gehört dann eine Winkelgenauigkeit von etwa
1'=1/60°.
Es heißt also sin(52°)=0,7880.
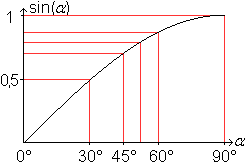
Mit dem Taschenrechner kann man sich für
eine Wertetabelle weitere Werte verschaffen und einen Graphen zeichnen.
Der folgende Graph entstand allerdings mit dem Programm Winplot (URL unten).
Kosinuswerte
top
Die Kosinusfunktion ist eng mit der Sinusfunktion verbunden.
... |
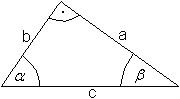Der Kosinuswert ist das Verhältnis der Ankathete
zur Hypotenuse.
In der Formelsprache heißt das cos(alpha)=b/c.
Dann gilt cos(alpha)=sin(beta)=sin(90°-alpha). |
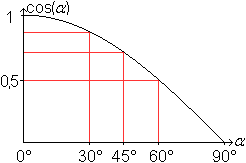
Da beta=90°-alpha gilt,
sehen Wertetabelle und Graph folgendermaßen aus.
| alpha |
0°
|
30°
|
45°
|
60°
|
90°
|
| sin(alpha) |
1
|
(1/2)sqrt(3)
|
(1/2)sqrt(2)
|
1/2
|
0
|
|
 |
Im Grunde ist die Kosinusfunktion
eine Abwandlung der Sinusfunktion.
Diese Aussage wird weiter unten noch deutlicher werden.
Erweiterung
des Definitionsbereichs top
D={alpha | 0<= alpha <=360°}
Eine Erweiterung des Definitionsbereichs erreicht man
mit folgender Definition, die nicht im Widerspruch zu den Überlegungen
oben stehen darf und auch nicht steht.
... ... |
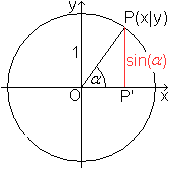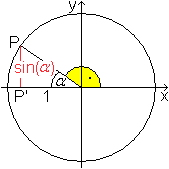
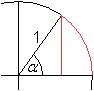
Man gibt in einem kartesischen Koordinatensystem einen
Kreis mit dem Radius 1 vor und einen Punkt P(x|y) auf der Kreisline. Verbindet
man diesen Punkt mit dem Nullpunkt O, so entsteht mit der positiven x-Achse
der Winkel alpha.
Der Sinus des Winkels alpha wird durch den y-Wert des
Punktes P angegeben, denn im rechtwinkligen Dreieck OP'P ist sin(alpha)=PP'/1=PP'. |
Der Sinus ist hier also eine Strecke, die in der Einheit
r=1 gemessen wird, insofern auch ein Seitenverhältnis.
... ... |
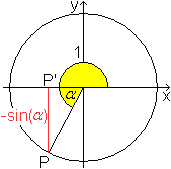
Wandert der Punkt P entgegen dem Uhrzeigersinn auf dem
Einheitskreis über den Winkel von 90° hinaus, so bleibt es bei
der Definition PP'=sin(alpha).
Links wird gezeigt, wie man die Sinuswerte der Winkel
zwischen 90° und 180° auf die Sinuswerte
spitzer Winkel
alpha zurückführt.
Es gilt sin(180-alpha) = sin(alpha). |
... ... |
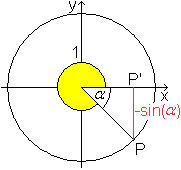
Links wird gezeigt, wie man die Sinuswerte der Winkel
zwischen 180° und 270° auf die Sinuswerte spitzer
Winkel alpha zurückführt.
Es gilt sin(180°+alpha)=-sin(alpha). |
... ... |
Links wird gezeigt, wie man die Sinuswerte der Winkel
zwischen 270° und 360° auf die Sinuswerte spitzer
Winkel alpha zurückführt.
Es gilt sin(360°-alpha)=-sin(alpha) |
... ... |
Der Sachverhalt wird noch einmal in einer Animation dargestellt.
(Das Bogenmaß eines Winkels wird schon einmal vorweggenommen.) |
Auf diese Weise wird der
Sinus für alle Winkel zwischen 0° und 360° erklärt.
D={alpha|
alpha beliebig}
Wandert der Punkt P von der x-Achse aus entgegen dem
Uhrzeigersinn, so wiederholen sich die Sinuswerte: sin(alpha+360°)=sin(alpha)
allgemeiner: sin(alpha+n*360°)=sin(alpha), n=1, 2,
3,...
Wandert der Punkt P von der
x-Achse aus
im Uhrzeigersinn, so werden die Winkel negativ. Auch
da definiert man den Sinuswert in gleicher Weise: sin(-alpha)=-sin(alpha).
Damit ist der Sinus für
alle Winkel definiert.
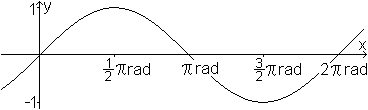
Ein Graph stellt diesen Sachverhalt noch einmal anschaulich
dar.
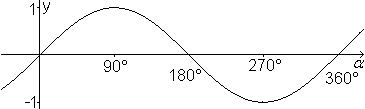
D=|R.
Es ist üblich und auch sinnvoll, die Winkel der
Sinusfunktion nicht im Gradmaß, sondern im Bogenmaß anzugeben.
Dann schreibt man f(x)=sin(x) an Stelle von f(alpha)=sin(alpha).
Der Definitionsbereich ist
D={x
|  }.
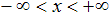Die Angabe der Einheit 1 Radiant (1 rad) ist entbehrlich,
wie man unter
Bogenmaß
auf meiner
Kreis-Seite nachlesen kann.
... ... |
Das Bogenmaß bietet sich auch deshalb an, weil
es sich auch im Einheitskreis wiederfindet. Die Größe eines
Winkels wird nämlich durch die Länge des Kreisbogens, der zum
Winkel gehört, bestimmt. Als Einheit der Längenmessung dient
der Radius des Kreises. |
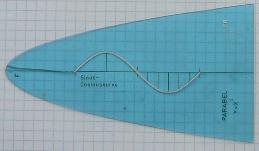
Das Bogenmaß bestimmt die Form des Graphen. Beim Gradmaß
liegt nicht fest, wo z.B. der Winkel 360° liegt.
So benutzen Schablonen zum Zeichnen der Sinuskurve das
Bogenmaß.
Kosinusfunktion
für D=|R.
Wie oben erwähnt, gilt für die Kosinusfunktion
cos(alpha)=sin(90°-alpha).
In diesem Zusammenhang heißt die Erweiterung der
Kosinusfunktion cos(x)=sin(pi/2-x)=sin(x+pi/2) mit D=|R. Der Graph geht
aus dem Graphen des Sinus durch Verschieben um pi/2 in -x-Richtung hervor.
Ermittlung
der Sinuswerte top
Funktionswerte mit dem Taschenrechner
Oben wurde schon beschrieben, wie man mit dem Taschenrechner
zu sin(52,0°)=0,7880 kommt.
Dabei muss man beachten, dass dieser im Grad-Modus steht.
Das erkennt man daran, dass im Display DEG steht. Das ist nach dem Einschalten
der Fall.
Will man den Sinuswert eines Winkels, der im Bogenmaß
angegeben ist, bestimmen, schaltet man mit der Taste DRG den Radiant-Modus
RAD ein. Dann ergibt sich z.B. sin(1 rad)=0,8415.
Funktionswerte
mit dem Tafelwerk
... ... |
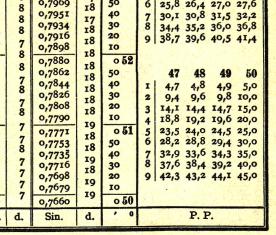In Vor-Taschenrechner-Zeiten standen
die Funktionswerte in einem Tafelwerk ("Logarithmentafeln") bereit.
Man erkennt links sin(52°)=0,7880
wieder.
Die Tabellen enthalten Sinuswerte für Winkel auf
1'=1/60° genau.
Für diese Genauigkeit benötigt man Zahlenspalten
wie rechts.
|
Nützlicher als der abgebildete
Tafelausschnitt waren umfangreiche Tabellen, die die Logarithmen trigonometrischer
Funktionen enthielten. Denn mit Hilfe der Logarithmen wurde früher
das Multiplizieren vermieden und durch das einfachere Addieren ersetzt,
wenn auch auf Kosten der Genauigkeit.
Berechnung
der Sinuswerte
Die Sinuswerte kann man nach der Taylor-Reihe berechnen.
sin(x) = x - (1/3!)x3
+ (1/5!)x5
-
(1/7!)x7
+ ...
Zur Herleitung der Formel
Die Taylor-Reihe lautet allgemein f(x)=f(a) + (1/1!)f'(a)(x-a)
+ (1/2!)f''(a)(x-a)2 + (1/3!)f'''(a)(x-a)3+ ...
Hier ist f(x)=sin x, f'(x)=cos(x), f''(x)=-sin(x), f'''(x)=-cos(x),
...
Daraus folgt f(0)=0, f'(0)=1, f''(0)=0, f'''(0)=-1, f(4)(0)=0,
f(5)(0)=1 ...
Dann ist sin(x) = x - (1/3!)x3
+ (1/5!)x5
-
(1/7!)x7+(1/9!)x9 - +..., wzbw.
Zahlenbeispiel
Der Taschenrechner liefert sin(52°)=sin(0,9076 rad)=0,7880.
Die Reihe liefert sin(0,9076 rad)=0,90757-0,12459+0,00513-0,00010+0,00000=0,7880.
Die Reihe konvergiert schnell.
Eigenschaften
der Sinusfunktion
top
Graph
Definitions-
und Wertebereich
Größtmöglicher Definitionsbereich
|
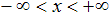
Wertebereich
-1< = sin(x) <= 1
|
Periode
Es gilt sin(alpha+360°)=sin(alpha)
oder sin(x+2pi)=sin(x).
Damit ist die Sinusfunktion eine
periodische Funktion mit der (kleinsten)
Periode
360° oder 2pi rad.
Amplitude
Die Amplitude ist 1.
Besondere Punkte
Nullstellen
xN=k*pi
|
Extrema
xE=(1/2)pi+k*pi
|
Wendepunkte
xW=k*pi
|
Die Variable k steht für ganze Zahlen.
Symmetrie
Die Sinusfunktion ist punktsymmetrisch
bezüglich des Nullpunkts. Es gilt sin(x)= - sin(-x).
Steigung
... ... |
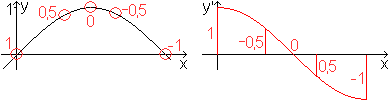Wie groß ist die Steigung der Sinuskurve in ihren
Punkten?
An bestimmten Stellen ist die Steigung zugänglich.
Man sieht so ein, dass die Steigung durch die Kosinusfunktion
beschrieben wird. |
Das zeigt die folgende Rechnung.
Es werden folgende Formeln vorausgesetzt.
|
lim[sin(x)/x]=1 für x gegen 0
|
sin(alpha)-sin(beta)=2sin(beta/2)cos(alpha/2)
|
Der Differenzenquotient ist
[sin(x+h)-sin(x)]/h={2sin(h/2)cos[(2x+h)/2]}/h={sin[(h/2)]/h}cos(x+h/2)
Strebt h gegen 0, so strebt sin(h/2)/(h/2) gegen 1 und
cos(x+h/2) gegen cos(x).
Ergebnis: Der Differenzenquotient strebt gegen cos(x),
f'(x)=cos(x).
Fläche
... ... |
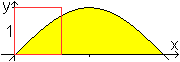Wie groß ist der Flächeninhalt des Flächenstücks
zwischen Sinuskurve und x-Achse?
Vermutung: Im Vergleich zum roten Einheitsquadrat dürften
es so etwa 2 Flächeneinheiten sein. |
Lösung
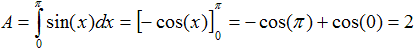Gut geschätzt.
Kurvenlänge
... ... |
Wie lang ist das Kurvenstück der Sinuskurve zwischen
zwei Nullstellen?
Vermutung: Verglichen mit der Einheitsstrecke auf der
y-Achse sind es etwa 4 Längeneinheiten. |
Lösung
| Der Ansatz ist |
 |
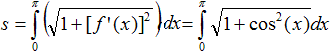Das Integral ist als elliptisches Integral nicht elementar
zu berechnen, aber näherungsweise über eine Reihe.
Ergebnis: Die Länge ist s=pi(1+1/4-3/64+5/256-175/16384+
-...) = 3,808 LE, wie in (2), Seite 469f, demonstriert wird.
Einige
trigonometrische Formeln top
Auf dieser Seite werden einige Formeln verwendet und
hier bewiesen.
Ich beschränke mich auf eine
Untersuchung im ersten Quadranten.
sin²(alpha)+cos²(alpha)=1
... |
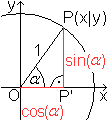Nach dem Satz des Pythagoras gilt
sin²(alpha)+cos²(alpha)=1. |
sin(2alpha)=2sin(alpha)cos(alpha)
... ... |
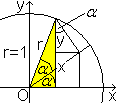Man zeichnet in die Figur des Einheitskreises die Winkel
alpha ein und ergänzt die Figur wie links.
Es gilt im gelben Dreieck sin(2alpha)=x+y. |
... ... |
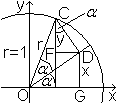Im rechtwinkligen Dreieck ODC gilt OD=cos(alpha), im
Dreieck OGD gilt sin(alpha)=x/OD.
Dann ist x=OD*sin(alpha)=sin(alpha)cos(alpha).
Im rechtwinkligen Dreieck ODC gilt DC=sin(alpha), im
Dreieck FDC gilt cos(alpha)=y/DC.
Dann ist y=DC*cos(alpha)=sin(alpha)cos(alpha). |
Damit gilt sin(2alpha)=x+y=2sin(alpha)cos(alpha).
cos(2alpha)=cos²(alpha)-sin²(alpha)
... ... |
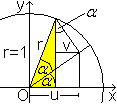Man zeichnet in die Figur des Einheitskreises die Winkel
alpha ein und ergänzt die Figur wie links.
Es gilt im gelben Dreieck cos(2alpha)=u-v. |
... ... |
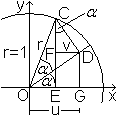Im rechtwinkligen Dreieck ODC gilt OD=cos(alpha), im
Dreieck OGD gilt cos(alpha)=u/OD.
Dann ist u=OD*cos(alpha)=cos²(alpha).
Im rechtwinkligen Dreieck ODC gilt DC=sin(alpha), im
Dreieck FDC gilt sin(alpha)=v/DC.
Dann ist v=DC*sin(alpha)=sin²(alpha). |
Damit gilt cos(2alpha)=u-v=cos²(alpha)-sin²(alpha).
Quelle:
(3), Seite 272
Allgemeine
Sinusfunktion top
Aus der Sinusfunktion geht die allgemeine Sinusfunktion
hervor. Sie hat die Form f(x)=a*sin(bx+c), wobei a, b und c reelle Zahlen
sind. Es ist sinnvoll zu fordern, dass sie nicht den Wert 0 annehmen.
Es stellt sich die Frage, welche Wirkung die Parameter
a, b und c haben, ausgehend von der Funktionsgleichung f(x)=sin(x)?
> Gibt man f(x)=a*sin(x)
vor, so bewirkt |a|>1 eine Streckung, |a|<1 eine Stauchung der Sinuskurve
in y-Achsen-Richtung.
Das illustrieren die folgenden vier Graphen.
... ... |
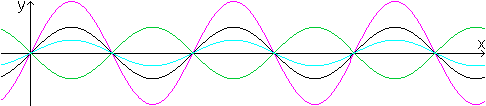f(x)=sin(x), f(x)=2sin(x),
f(x)=(1/2)sin(x),
f(x)=-sin(x).. |
> Gibt man f(x)=sin(bx) vor,
so bewirkt |b| eine Veränderung der Periode 2pi auf 2pi/|b|.
Das illustrieren die folgenden vier Graphen.
... .... |
f(x)=sin(x), f(x)=sin(2x),
f(x)=sin[(1/2)x],
f(x)=sin(-x).... |
> Gibt man f(x)=sin(x+c)
vor, so bewirkt c eine Verschiebung des Graphen um c in den x-Achsen-Richtungen.
Das illustrieren die folgenden vier Graphen.
... ... |
f(x)=sin(x), f(x)=sin(x+2),
f(x)=sin(x+1/2),
f(x)=sin(x-1) |
Beispiel
... ... |
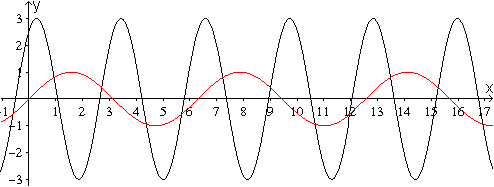f(x)=sin(x)
f(x)=3sin(2x+1) oder f(x)=3sin[2(x+1/2)]
Die Amplitude ist 3, die Periode ist 2 und
die Verschiebung in -x-Richtung ist 1/2.
................................................................................... |
Kombination
von Sinuskurven
top
sin(x)+cos(x)
... ... |
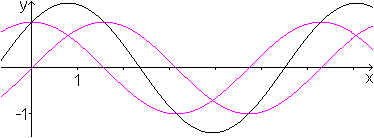Die roten Kurven sind die Graphen des Sinus und des Kosinus.
Die schwarze Kurve entsteht durch Überlagerung beider Kurven und ist
eine Sinuskurve. Man kann ablesen: Die Periode ist 2pi, der Scheitelwert
sqrt(2) und die Verschiebung in -x-Richtung ist pi/2.
Damit ergibt sich die Gleichung sin(x)+cos(x)=sqrt(2)sin(x+pi/2). |
sin(x)cos(x)
... ... |
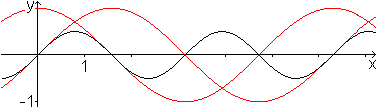Die roten Kurven sind die Graphen des Sinus und des Kosinus.
Die schwarze Kurve entsteht durch Überlagerung beider Kurven und ist
eine Sinuskurve. Man kann ablesen: Die Periode ist pi und der Scheitelwert
ist 1/2.
Damit ergibt sich die Gleichung sin(x)cos(x)=(1/2)sin(2x),
eine bekannte trigonometrische Formel. |
sin(x)sin(x)
.. .... |
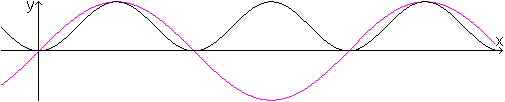Der gegebene Funktionsterm ist f(x)=sin²(x).
Es gilt, wie in der Zeichnung abzulesen,
sin²(x)=1/2-(1/2)cos(2x). |
Die Gleichung folgt aus den trigonometrischen Formeln sin²(x)+cos²(x)=1
und cos(2x)=cos²(x)-sin²(x).
Schwebung
... ... |
f(x)=sin(12x).
Der Graph von f(x)=sin(13x) ist
fast identisch. |
... ... |
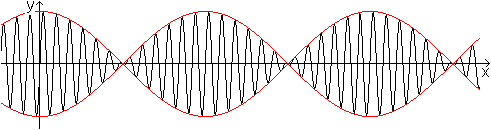f(x)=sin(12x)+sin(13x)
f1(x)=+cos(x/2)
und f2(x)=+cos(x/2). |
Es überlagern sich zwei Sinuskurven, deren Perioden
sich nur wenig unterscheiden.
Es gilt die trigonometrische Formel sin(x)+sin(y)=2cos[(x-y)/2]sin[(x+y)/2].
In diesem Sonderfall ist sin(13x)+sin(12x)=2cos(x/2)sin(25x/2).
Darstellung
periodischer Funktionen
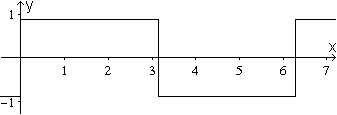
Eine Rechteckkurve kann man angenähert
durch
Überlagerung von Sinuskurven darstellen.
Es folgt ein Beispiel.
|
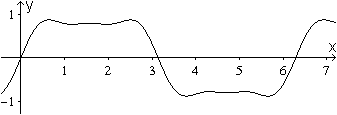
f(x)=sin(x)+0,5sin(3x)+0,3sin(5x)
|
Im Hintergrund steht die
Fourierreihe. Eine periodische Funktion kann angenähert durch eine
Reihe von Sinusfunktionen in beliebiger Genauigkeit beschrieben werden.
Arkussinus
top
... ... |
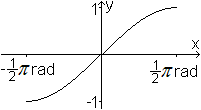Die Sinusfunktion ist als Ganzes nicht umkehrbar, denn
z.B. gibt es zu y=0 beliebig viele x-Werte, nämlich die Nullstellen.
Schränkt man dagegen den Definitionsbereich auf -(1/2)pi<=x<=(1/2)pi
ein, so gibt es zu jedem x-Wert genau einen y-Wert.
In diesem Bereich ist sie also umkehrbar. |
... ... |
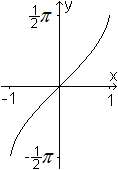Man erhält den Graphen der Umkehrfunktion, indem
man die Sinuskurve an der ersten Winkelhalbierenden spiegelt.
Für den Funktionsterm der Umkehrfunktion gibt es
die Symbole arc sin(x) oder sin-1(x).
Der Definitionsbereich ist D={x| -1 <= x <= 1},
der Wertebereich W={y| (1/2)pi <= y <= (1/2)pi}. |
Winkel
mit dem Taschenrechner
Gibt man in den Taschenrechner einen Sinuswert zwischen
-1 und +1 ein, so wird nach Maßgabe der Umkehrfunktion nur ein Winkel
zwischen -(1/2)pi und +(1/2)pi bzw. -90° und +90° ausgegeben.
So erhält man zum Sinuswert 0,7880 den Winkel 52°
über die Tastenfolge (2nd) (sin)...
Man schreibt arc sin(0,7880)=52°.
Zwei weitere Beispiele sind arc sin(0,3333)= 19,5°
und arc sin(-0,3333)= -19,5°.
Figuren in
der Sinus-Linse
top
Größtes Rechteck
Die Graphen der Funktionen f(x)=sin(x) und g(x)=-sin(x)
bilden im Bereich 0 <= x <= pi eine Linse.
... ... |
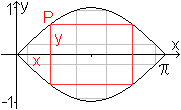Passt man in die Linse Rechtecke ein, so dass die Eckpunkte
auf den Sinuskurven wie links liegen, so stellt sich die Frage nach dem
Rechteck mit dem größten Flächeninhalt. |
Lösung
Der Ansatz ist A=(pi-2x)(2y)
Mit y=sin(x) gilt A(x)=2pi*sin(x)-4x*sin(x).
Die Ableitung ist A'(x)=2pi*cos(x)-4*sin(x)-4x*cos(x).
A'(x)=0 führt zu pi*cos(x)-2sin(x)-2x*cos(x)=0.
Das ist eine transzendente Gleichung, die i.a. nur näherungsweise
gelöst werden kann.
... ... |
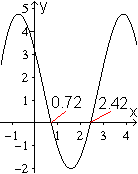Zur Lösung der Gleichung pi*cos(x)-2sin(x)-2x*cos(x)=0
gelangt man z.B., indem man die Nullstelle der Funktion f(x)=pi*cos(x)-2sin(x)-2x*cos(x)=0
bestimmt.
Dazu werden mit dem Zeichenprogramm Winplot der Graph
gezeichnet und die Nullstelle abgelesen: x1=0,72. - Auch die
zweite Nullstelle x2=2,42=pi-x1 passt zum Problem.
Ergebnis: Das Rechteck 1,70 mal 1,32 ist das größte. |
Quadrat
... ... |
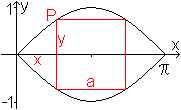Soll das rote Rechteck von oben zu einem Quadrat werden,
muss
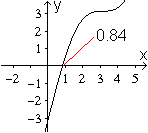
2y=pi-2x oder 2sin(x)-pi+2x=0 gelten. Wie beim Problem
des größten Rechtecks wird die Gleichung graphisch gelöst.
Es ergibt sich x=0,84 und dann als Seite des Quadrats
a=pi-2x=1,46 (LE). |
... ... |
Fünf
weitere Figuren
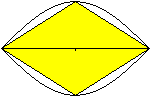
Raute
|
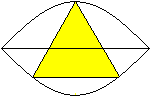
Gleichseitiges Dreieck
|
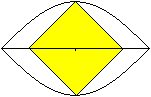
Quadrat auf der Spitze
|
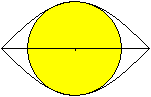
Kreis
|
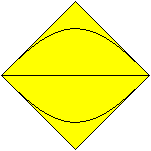
"Um-Quadrat"
|
Übersicht
über die trigonometrischen Funktionen top
Neben der Sinusfunktion gibt es fünf weitere trigonometrische
Funktionen, bei denen einem Winkel im rechtwinkligen Dreieck andere Seitenverhältnisse
zugeordnet werden.
|
|
Sinus
sin(x)=a/c
|
Kosinus
cos(x)=b/c
|
Tangens
tan(x)=a/b
|
Kotangens
cot(x)=b/a
|
Sekans
sec(x)=c/a
|
Kosekans
csc(x)=c/b
|
Es gilt 0 <= x <= (1/2)pi.
Alle Funktionswerte findet man am Einheitskreis als Strecken,
hier im 1.Quadranten eingezeichnet.
|
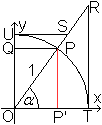
sin(x)=PP'
|
cos(x)=QP
|
tan(x)=TR
|
cot(x)=US
|
sec(x)=OR
|
csc(x)=OS
|
Es gilt .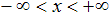
Alle Graphen in einem Bild
|
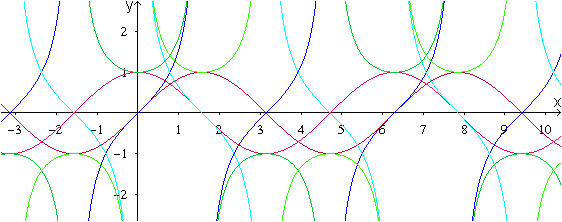
sin(x) und cos(x) in Rot
tan(x) und cot(x) in Blau
sec(x) und csc(x) in Grün |
Alle Funktionswerte lassen
sich auf Sinuswerte zurückführen, denn es gelten folgende Formeln.
sin(x)
vorgegeben |
cos(x)
=sqrt[1-sin²(x)] |
tan(x)
=sin(x)/sqrt[1-sin²(x)] |
cot(x)
=sqrt[(1-sin²(x)]/sin(x) |
sec(x)
=1/sqrt[1-sin²(x)] |
csc(x)
=1/sin(x) |
Die Formel sin²(x)+cos²(x)=1
wird in der Tabelle verwendet.
In der Schule finden heute
nur der Sinus, der Kosinus und der Tangens Verwendung.
Der Kotangens ist aus den Lehrbüchern weitgehend
verschwunden.
Ich entdeckte den Sekans und den Kosekans erstmals in
einem englischen Lehrbuch.
Flächen
im Raum der Form z=f(x,y) top
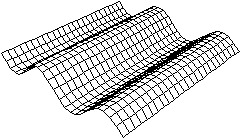
z=sin(x)
|
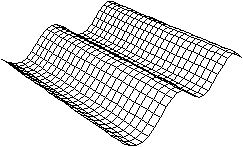
z=sin(y)
|
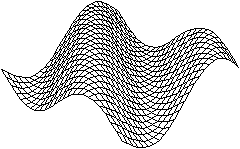
z=sin(x+y)
|
z=sin(x)sin(y)
|
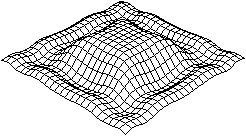
z=[sin(x²)+sin(y²)]/(x²+y²)
|
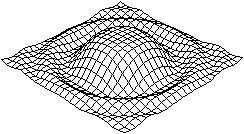
z=sin(x²+y²)/(x²+y²)
|
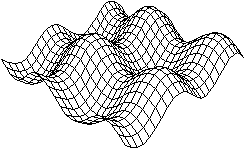
z=sin(x)+sin(y)
|
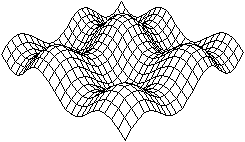
z=sin(x)-sin(y)
|
Figuren aus Sinuslinien
top
Der
Sinus an anderen Stellen meiner Homepage top
Sinussatz
... |
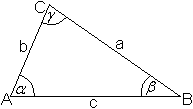a:b:c=sin(alpha):sin(beta):sin(gamma) |
Mehr auf meiner Seite
Allgemeines
Dreieck
Parameterdarstellungen
von Kurven
x(t)=4r*cos(t/3)-a*cos(4t/3)
y(t)=4r*sin(t/3)-a*sin(4t/3)
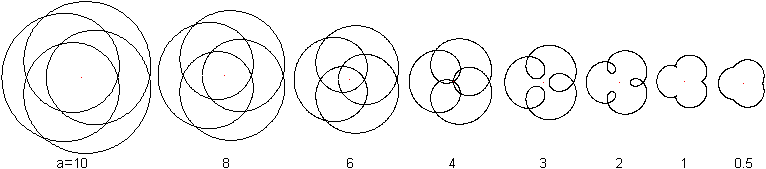Mehr auf meiner Seite Dreistrahlige
Figuren
x(t)=5r*cos(t/4)-a*cos(5t/4)
y(t)=5r*sin(t/4)-a*sin(5t/4)
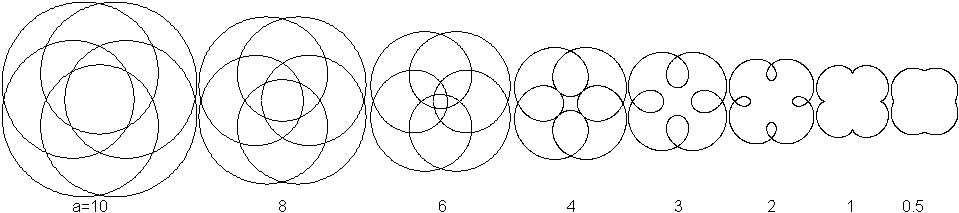
Mehr auf meine Seite
Vierstrahlige
Figuren
Darstellungen
in Polarkoordinaten
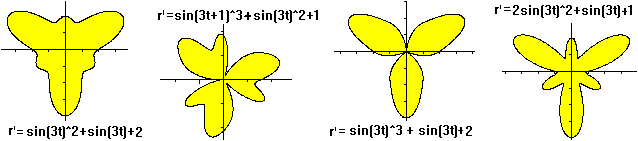Mehr auf meiner Seite Dreistrahlige
Figuren
Eierketten
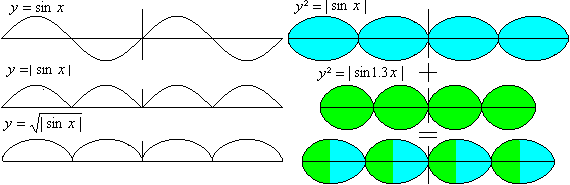
Mehr auf meiner Seite
Eilinien.
Erzeugung
einer Herzfigur
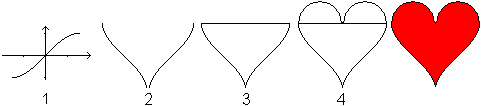
Mehr auf meiner Seite
Herzkurven
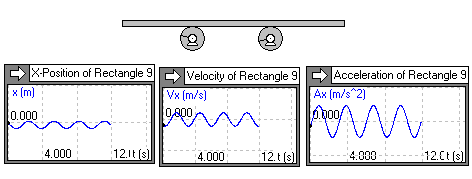
Eine
Sinusschwingung
Mehr auf meiner Seite
Eine Schwingung
durch Reibung
Sinusfunktion
im Internet
top
Deutsch
leifiphysik (Rupprecht-Gymnasium in München)
Die
Sinusfunktion
Wikibooks
Differentiation
der Sinusfunktion
Wikipedia
Sinus
und Kosinus, Arkussinus
und Arkuskosinus, Sinus
versus und Kosinus versus, SOHCAHTOA,
Formelsammlung
Trigonometrie, Fourierreihe,
Sinuston
, Ton
440Hz - hörbar, Schwebung
Englisch
Eric W. Weisstein (MathWorld)
Sine,
Inverse
Sine, Inverse
trigonometric functions, Simple
Harmonic Motion, Fourier
Series
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Sine,
Inverse
trigonometric function, Sine
quadrant, Versine,
Beat
(acoustics),
List
of trigonometric identities
Referenzen
top
(1) F.G.Gauß: Vierstellige logarithmische und trigonometrische
Tafeln, Stuttgart 1953
(2) Georg Ulrich / Paul Hoffmann: Differential- und Integralrechnung
zum Selbstunterricht, Hollfeld
[ISBN 3 8044 0575 4]
(3) Autorengemeinschaft: Algebra und Geometrie
für Ingenieure, Frankfurt/M Zürich 1966
[ISBN 978-3-87144-107-3]
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
http://www.mathematische-basteleien.de/
© 2011 Jürgen Köller
top |
...
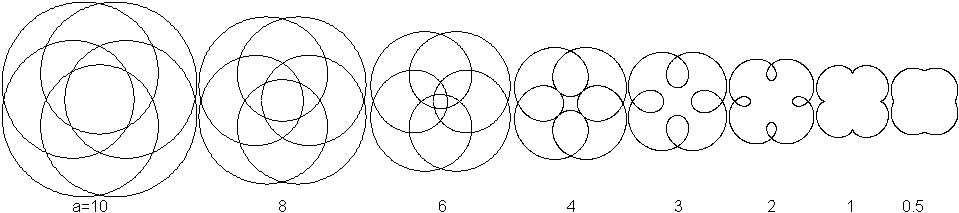
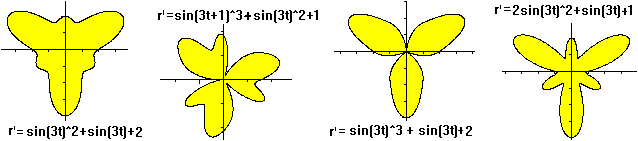
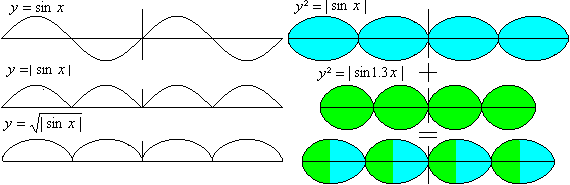
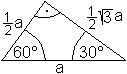
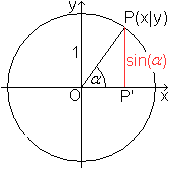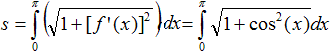
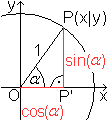
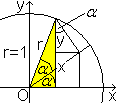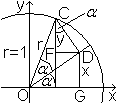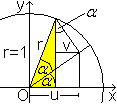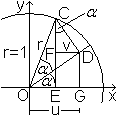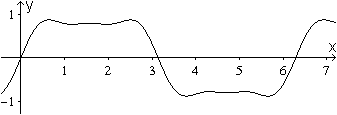
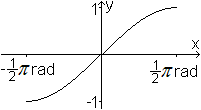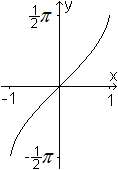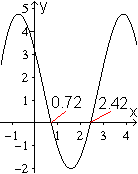