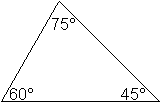|
Was ist das allgemeine Dreieck?
...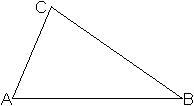 ... ... |
Das allgemeine Dreieck entsteht, wenn man drei beliebige,
nicht auf einer Geraden liegende Punkte A, B und C durch Strecken verbindet.
"Allgemein" soll heißen, dass das Dreieck keine
besonderen Eigenschaften hat und dass sich somit die Aussagen auf beliebige
Dreiecke beziehen. |
Ich beschränke mich
auf dieser Seite auf spitzwinklige Dreiecke.
Die Aussagen lassen sich auch auf stumpfwinklige Dreiecke,
also Dreiecke mit einem stumpfen Innenwinkel, übertragen. Die Zeichnungen
und Beweise müssten dann angepasst werden. Das will ich mir ersparen.
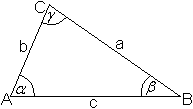
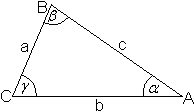
Bezeichnungen top
Man bezeichnet üblicherweise aus praktischen Gründen
die Eckpunkte eines Dreiecks mit A, B und C, die Seiten mit a, b und c
und die Innenwinkel mit alpha, beta und gamma.
> Zu Punkt A gehört der Winkel alpha.
> Die Seite a liegt dem Punkt A gegenüber.
> Die Punkte A, B und C sind entgegengesetzt dem Uhrzeigersinn
angeordnet.
> Die Seite c liegt horizontal.
Wo z. B. der Punkt A liegt, hängt offenbar vom Kulturbereich
ab, wie aus den entsprechenden Wikipedia-Seiten hervorgeht.
deutsch
|
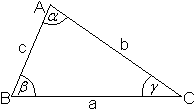
französisch
|
italienisch
|
...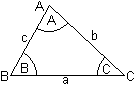 ... ... |
Im englischsprachigen Bereich werden auch die Winkel
manchmal mit A, B und C bezeichnet (2). |
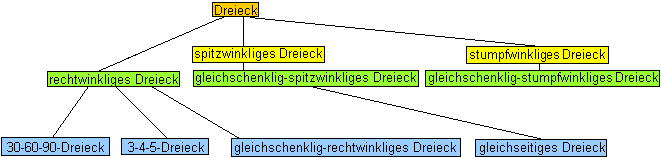
Besondere Dreiecke
top
Die folgenden sechs Dreiecke haben besondere Eigenschaften,
die in den Namen zum Ausdruck kommen.
Übersicht
Formeln zum Dreieck
top
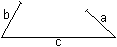
Dreiecksungleichungen
Für ein Dreieck gilt a+b>c, a+c>b
und b+c>a.
...
 ...
a+b<c ...
a+b<c
|
Die Ungleichungen besagen, dass im Dreieck die Summe
der Längen zweier Seiten stets größer ist als die Länge
der dritten Seite.
Durch diese Bedingungen wird sichergestellt, dass ein
Dreieck aus drei Seiten überhaupt entstehen kann. |
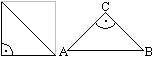
Satz
von der Winkelsumme im Dreieck
Der Satz lautet alpha+beta+gamma=180°.
...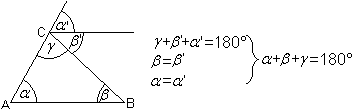 ... ... |
Der Beweis geht aus der Skizze hervor.
Die Formel folgt aus den Aussagen
>Der gestreckte Winkel hat das Winkelmaß 180°.
>Wechselwinkel an Parallelen sind gleich.
>Stufenwinkel an Parallelen sind gleich. |
Sinussatz
Er lautet a:b=sin(alpha):sin(beta), a:c=sin(alpha):sin(gamma)
und b:c=sin(beta):sin(gamma).
Herleitung
...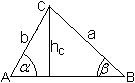 ... ... |
Aus hc=a*sin(beta)und hc=b*sin(alpha)
folgt a*sin(beta)=b*sin(alpha) oder a:b=sin(alpha):sin(beta).
Zeichnet man hb ein, so gelangt man entsprechend
zu a:c=sin(alpha):sin(gamma).
Die Höhe ha führt zu b:c=sin(beta):sin(gamma). |
Die drei Formeln fasst man zu a:b:c=sin(alpha):sin(beta):sin(gamma)
zusammen.
Kosinussatz
Er lautet a²=b²+c²-2bc*cos(alpha),
b²=a²+c²-2ac*cos(beta)
und c²=a²+b²-2ab*cos(gamma).
Herleitung
...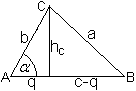 ... ... |
Es gelten die Formeln a²=(c-q)²+hc²,
q=b*cos(alpha)
und
hc=b*sin(alpha)
und.
Das bedeutet a²=(c-q)²+hc²=c²-2cq+q²+hc²
=c²-2cb*cos(alpha)+b²*cos²(alpha)+b²*sin²(alpha)=b²+c²-2cb*cos(alpha). |
Die Formeln b²=a²+c²-2ac*cos(beta) und c²=a²+b²-2ab*cos(gamma)
erhält man, wenn man die anderen Höhen betrachtet.
Aus
dem Sinus- und dem Kosinussatz gehen drei weitere Formeln hervor.
Mollweidesche Formeln
...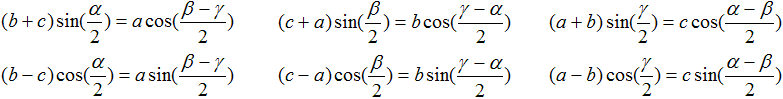
Tangenssatz
...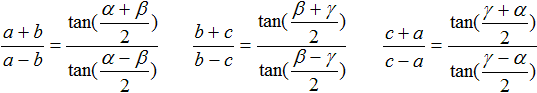
Halbwinkelsatz
...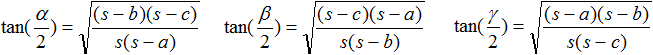 |
mit 2s=a+b+c |
Da in den Formeln die halben
Winkel auftauchen, sind sie für praktische Dreiecksberechnungen von
Dreiecken mit kleinen Winkeln und Winkeln nahe an 90° geeignet (1).
Einen Beweis der drei Sätze findet man bei Thomas
Steinfeld (Wurzelzieher Mathepedia) (URL unten).
Grundaufgaben top
Übersicht
Will man ein Dreieck festlegen, genügt es, von den
sechs Stücken a, b, c, alpha, beta und gamma nur drei Stücke
zu kennen.
Die übrigen findet man durch Rechnung (oder Zeichnung).
Es gibt 20 Möglichkeiten, drei von sechs Stücken
herauszugreifen. Diese Anzahl wird mit Hilfe des Binomialkoeffizienten
C(n,k) bestimmt. Es gilt C(n.k)=n!/[k!(n-k)!] und hier speziell C(6,3)=6!/[3!(6-3)!]=(4*5*6)/(2*3)=20.
Und das sind die 20 Möglichkeiten.
a-b-c,
a-b-alpha, a-b-beta, a-b-gamma,
a-c-alpha, a-c-beta, a-c-gamma,
a-alpha-beta, a-alpha-gamma,
a-beta-gamma |
b-c-alpha, b-c-beta, b-c-gamma,
b-c-beta, b-c-gamma
b-beta-gamma |
c-alpha,-beta, c-alpha-gamma,
c-beta-gamma |
alpha-beta-gamma |
Ordnet man die Tripel nach der Lage der Seiten und Winkel
zueinander, so gelangt man zwangsläufig zu den vier Grundaufgaben
SSS, WSW, SWS und SgSW. Bei ihnen werden durch drei gegebene
Größen die übrigen eindeutig bestimmt, wie die folgenden
Überlegungen zeigen.
1.
Grundaufgabe SSS
Gegeben sind die drei Seiten.
... |
Ein Fall
a-b-c
 |
Zur Lösung
Gegeben sind a, b und c, gesucht sind alpha, beta und
gamma.
... |
Es gelten die drei Formeln des
Kosinussatzes.
a²=b²+c²-2bc*cos(alpha)
b²=a²+c²-2ac*cos(beta)
c²=a²+b²-2ab*cos(gamma)
Aus ihnen berechnet man die Winkel.
 |
Es muss die Dreiecksungleichung erfüllt werden, damit
es überhaupt ein Dreieck gibt.
2.
Grundaufgabe WSW
Gegeben sind eine Seite und zwei Winkel.
... |
9 Fälle
alpha-c-beta, beta-a-gamma, gamma-b-alpha,
c-beta-gamma, a-gamma-alpha, b-alpha-beta,
c-alpha-gamma, b-gamma-beta,
a-beta-alpha
 |
Der Fall WWS muss nicht gesondert aufgeführt werden,
weil man immer den Winkel zwischen den Seiten aus den gegebenen nach der
Winkelsumme im Dreieck berechnen kann.
Zur Lösung der exemplarischen
Aufgabe
Gegeben sind c, alpha und gamma, gesucht sind a,b und
beta.
... ... ... |
Den Winkel beta berechnet man aus der Formel alpha+beta+gamma=180°.
Die Seite a berechnet man nach dem Sinussatz a:sin(alpha)=c:sin(gamma).
Die Seite b berechnet man nach dem Sinussatz b:sin(beta)=c:sin(gamma). |
3.
Grundaufgabe SWS
Gegeben sind zwei Seiten und der eingeschlossene Winkel.
...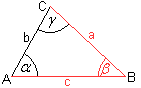 |
3 Fälle
c-beta-a, a-gamma-b, b-alpha-c
 |
Zur Lösung der exemplarischen
Aufgabe
Gegeben sind die Seiten a ,c und beta, gesucht sind b,
alpha und gamma.
... |
Die Seite b berechnet man nach dem Kosinussatz b²=a²+c²-2ac*cos(beta).
Den Winkel gamma berechnet man nach dem Sinussatz sin(gamma):sin(beta)=c:b.
Den Winkel alpha berechnet man nach alpha+beta+gamma=180°.
 |
4.
Grundaufgabe SgSW
Gegeben sind ein Winkel, eine anliegende und eine zu
ihr größere, dem Winkel gegenüberliegende Seite.
...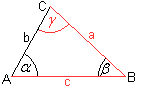 |
6 Fälle
c-a-gamma, a-b-alpha, b-c-beta,
c-a-alpha, b-a-beta, c-b-gamma
 |
...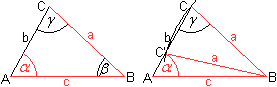 ... ... |
Sind die Stücke a, c und alpha gegeben und gilt
a<c, so gibt es offenbar zwei Dreiecke mit diesen Stücken, nämlich
die Dreiecke ABC und ABC'. |
Ein Kreis um Punkt B mit dem Radius a führt zu zwei
Schnittpunkten C und C'.
Deshalb ist die Zusatzbedingung a>c notwendig, um Eindeutigkeit
zu erreichen.
Zur Lösung der exemplarischen
Aufgabe
Gegeben sind a,c und gamma, gesucht sind b, alpha und
beta.
... |
Den Winkel alpha berechnet man nach dem Sinussatz sin(alpha):sin(gamma)=a:c.
Den Winkel beta berechnet man nach alpha+beta+gamma=180°.
Die Seite b berechnet man nach dem Sinussatz b:c=sin(beta):sin(gamma).
 |
... ... ... |
Sind a, c und alpha gegeben, so gilt sin(gamma):sin(alpha)=a:c.
Dann ist sin(gamma)=(a:c):sin(alpha). Ist
a<c, so ist a:c>1 und auch (a:c):sin(alpha)<1
sin(gamma)<1 bedeutet, dass es zwei Winkel gamma gibt,
eine spitzen und einen stumpfen. Das zeigt auch die Zeichnung. |
Der
Fall WWW
Der Fall, dass nur die drei Winkel gegeben sind, ist
zu streichen. Drei Winkel legen kein Dreieck eindeutig fest.
Dreiecke, die in entsprechenden Winkeln übereinstimmen,
sind nur ähnlich.
Kongruenz-
und Ähnlichkeitssätze top
Zwei Dreiecke sind kongruent, wenn sie in Form und Größe
übereinstimmen, also in allen sechs Stücken.
...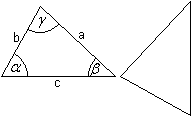 ... ... |
Nach den Überlegungen zu den Grundaufgaben kann
man vier Kongruenzsätze formulieren.
Zwei Dreiecke sind schon kongruent, wenn sie in drei
Stücken übereinstimmen, und zwar wie in den Grundaufgaben SSS,
WSW, SWS, SgSW beschrieben. |
...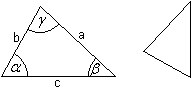 ... ... |
Zwei Dreiecke sind ähnlich, wenn sie in der Form
übereinstimmen.
Die Form aber stimmt überein, wenn entsprechende
Winkel gleich sind.
Es gibt drei weitere Ähnlichkeitssätze in Anlehnung
an die Grundaufgaben SSS, SWS, SgSW. |
Flächeninhalt
eines Dreiecks top
Grundformel
.....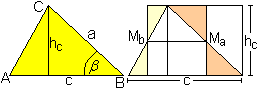 . . |
Der Flächeninhalt eines Dreiecks ist A=(1/2)chc=(1/2)ac*sin(beta). |
Beweis
Man zeichnet die Mittellinie MaMc
ein, die halb so groß wie die gegenüberliegende Seite c ist,
und ein Rechteck mit den Seiten c/2 und hc. Wegen der Kongruenz
der farbigen Paare von Dreiecken ist die Dreiecksfläche gleich der
Rechteckfläche (1/2)chc, wzbw.
In Analogie gilt A=(1/2)aha=(1/2)ab*sin(gamma)
und A=(1/2)bhb=(1/2)bc*sin(alpha).
Heronsche
Formel
... ... ... |
Sind die Seiten a,b und c des Dreiecks gegeben, so errechnet
sich der Flächeninhalt nach der heronschen Formel A=sqrt[s(s-a)(s-b)(s-c)]
mit s=(1/2)(a+b+c).
Einen Beweis findet man bei Arndt Brünner (URL unten) |
Flächeninhalt
über Koordinaten
Ist ein Dreieck ABC in einem kartesischen Koordinatensystem
gegeben, so lässt sich der Flächeninhalt mit Hilfe der Koordinaten
der Punkte über drei Trapeze berechnen.
...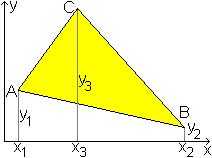 ... ... |
Es seien A(x1|y1), B(x2|y2)
und C(x3|y3) die Eckpunkte des Dreiecks.
Dann gilt nach der Zeichnung A=(1/2)(y1+y3)(x3-x1)+(1/2)(y2+y3)(x2-x3)-(1/2)(y1+y2)(x2-x1).
Man erhält A=(1/2)[x1(y2-y3)+x2(y3-y1)+x3(y1-y2)]. |
Besondere
Linien im Dreieck top
Übersicht
Nach der Tradition gibt es vier besondere Linien im Dreieck.
...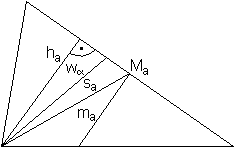 ... ... |
>Die Höhe h geht durch einen Eckpunkt und steht senkrecht
auf der Gegenseite.
>Die Winkelhalbierende w halbiert einen Innenwinkel.
>Die Seitenhalbierende s geht durch einen Eckpunkt und halbiert
die Gegenseite.
>Die Mittelsenkrechte m geht durch die Mitte einer Seite und
steht senkrecht auf ihr. |
Jede Transversale einer Art
kommt 3x vor. Zeichnet man sie ein, so schneiden sie sich in einem Punkt.
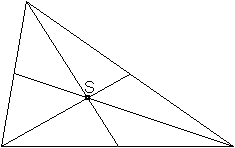
Seitenhalbierenden
|
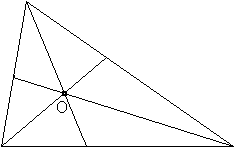
Winkelhalbierenden
|
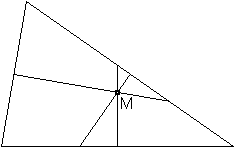
Mittelsenkrechte
|
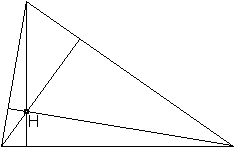
Höhen
|
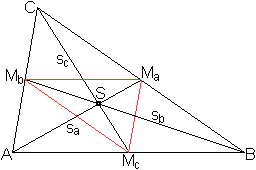
Seitenhalbierende
im Dreieck
...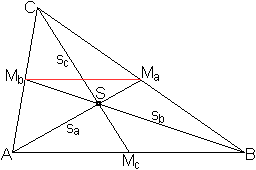 ... ... |
Der Schnittpunkt der Seitenhalbierenden ist der Schwerpunkt
des Dreiecks.
Die Figur wird um eine Mittelparallele ergänzt.
Man erhält sie, indem man zwei Seitenmitten miteinander verbindet.
Die Mittelparallele MaMb ist halb
so groß wie die nicht anliegende Seite AB. |
Es gilt nun: Die Seitenhalbierenden
oder Schwerlinien teilen sich im Verhältnis 2:1.
Beweis
Nach dem zweiten Strahlensatz ist SA:SMa=AB:MaMb=AB:(AB/2)=2:1,
wzbw.
Entsprechend verfährt man mit den beiden anderen
Seitenhalbierenden.
Die Längen der Seitenhalbierenden
errechnen sich nach den folgenden Formeln.
|
sa²=b²/2+c²/2-a²/4
|
sb²=a²/2+c²/2-b²/4
|
sc²=a²/2+b²/2-c²/4
|
Die Formeln sind eine Anwendung des Satzes von Stewart. Er
wird auf der Seite von Peter Andree (URL unten) bewiesen und zur
Herleitung dieser Formeln verwendet.
Winkelhalbierende
im Dreieck
... ... ... |
Es gilt: Die Winkelhalbierende schneiden sich im Mittelpunkt
des Inkreises.
Die Winkelhalbierende ist der geometrische Ort aller Punkte,
die von den Schenkeln eines Innenwinkels den gleichen Abstand haben.
Der Schnittpunkt O hat dann von allen Schenkeln den gleichen
Abstand. |
Jede Winkelhalbierende (eines Innenwinkels) im Dreieck
teilt die gegenüberliegende Seite im Verhältnis der anliegenden
Seiten. Das heißt in der Formelsprache a:b=c2:c1.
...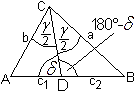 ... ... |
Beweis: Nach dem Sinussatz ist sin(180°-delta):sin(gamma/2)=a:c2
und in(delta):sin(gamma/2)=b:c1. Wegen sin(180°-delta)=sin(delta)
ist a:c2=b:c1 oder a:b=c:c1, wzbw. |
Entsprechende Formeln gelten für die beiden übrigen
Winkelhalbierenden.
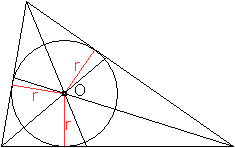
Für den Radius des Inkreises
gilt r=(2A)/(a+b+c) oder r=2*sqrt[s(s-a)(s-b)(s-c)]/s.
Beweis
... ... ... |
Man kann den Flächeninhalt eines Dreiecks auch mit
Hilfe des Radius bestimmen. Es gilt A=(1/2)ar+(1/2)br+(1/2)cr. Daraus ergibt
sich für den Radius r=(2A)/(a+b+c).
Berücksichtigt man die heronsche Flächenformel
A=sqrt[s(s-a)(s-b)(s-c)] mit s=(1/2)(a+b+c) von oben, so ist r=2*sqrt[s(s-a)(s-b)(s-c)]/s,
wzbw. |
Die Längen der Winkelhalbierenden
errechnen sich nach den folgenden Formeln.
|
walpha2=bc{[1-[a/(b+c)]²}
|
wbeta2=ac{[1-[a/(a+c)]²}
|
wgamma2=ab{[1-[a/(a+b)]²}
|
Die Formeln sind eine Anwendung des Satzes von Stewart. Er
wird auf der Seite von Peter Andree (URL unten) bewiesen und zur
Herleitung dieser Formeln verwendet.
Mittelsenkrechte
im Dreieck
...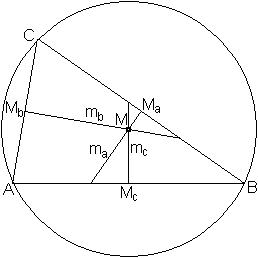 ... ... |
Der Schnittpunkt der Mittelsenkrechten eines Dreiecks
ist der Mittelpunkt des Umkreises.
Es gelten die Formeln R=(1/2)a/sin(alpha)=(1/2)b/sin(beta)=(1/2)c/sin(gamma). |
Beweis
...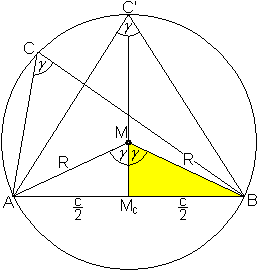 ... ... |
Man verlängert McM über M hinaus
und erhält Punkt C' und verbindet C' mit A und B.
Das gleichschenklige Dreieck ABC' ist entstanden.
Der Winkel an der Spitze ist gamma, da die Winkel ACB
und AC'B über der gleichen Sehne liegen und als Umfangswinkel gleich
sind.
Man verbindet M mit A und B.
Das gleichschenklige Dreieck ABM mit den Schenkeln R
ist entstanden.
Der Winkel an der Spitze ist als Mittelpunktwinkel über
AB gleich 2*gamma.
Im gelben Dreieck kann man sin(gamma)=(c/2)/R ablesen.
Das führt zu R=(1/2)c/sin(gamma). |
Entsprechend beweist man R=(1/2)a/sin(alpha)=(1/2)b/sin(beta).
Höhen
im Dreieck
... .... ....
|
Bei meinen Recherchen habe ich festgestellt, dass es
zum Thema Höhen im Dreieck viel Material gibt. Deshalb habe
ich das Kapitel Höhen im Dreieck ausgegliedert.
Da findet man auch die Aussage, dass der Höhenschnittpunkt
H, der Umkreismittelpunkt M und den Schwerpunkt S auf einer Geraden liegen.
- Es gilt HS=2*SM. |
Es gibt im Internet eine
Online-Liste mit mehr als 3500 (!) ausgezeichneten Dreieckspunkten. Das
ist die Encyclopedia of Triangle Centers (ETC), betreut von Clark Kimberling,
Professor für Mathematik an der University of Evansville (URL unten).
Die vier besprochenen Punkte bilden die ersten vier:
O=X(1), S=X(2), M=X(3) und H=X(4).
Mittendreieck
... ... ... |
Verbindet man die Mittelpunkte der Seiten, so entsteht
im Inneren ein halb so großes, ähnliches Dreieck, das Mittendreieck.
Entsprechende Seiten liegen parallel.
Weiter entstehen drei zum Mittendreieck kongruente Dreiecke
in den Ecken des Ausgangsdreiecks. |
Konstruktion
eines Dreiecks
top
Oben wird darauf eingegangen, wie man die Grundaufgaben
rechnerisch löst. Früher nahmen die zeichnerischen Lösungen
im Anfangsunterricht Geometrie viel Raum ein. Die Regel war, für Dreieckskonstruktionen
nur Zirkel und Lineal zu verwenden. Sind nur die Seiten oder Innenwinkel
gegeben, so sind die Konstruktionen einfach. Man geht von einer Seite aus
und findet den dritten Punkt über das Antragen von Winkeln und das
Zeichnen von Kreisen mit einer Seitenlänge als Radius. Anspruchsvoller
und oft nicht ohne Reiz sind Konstruktionen, wenn man weitere Größen
zulässt.
Das sind vier typische Aufgaben aus einem alten Lehrbuch
von 1952.
| Gegeben: |
...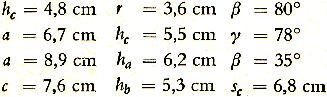 ... ... |
Neben den Stücken sind hier auch der Radius des
Umkreises, die Höhe und die Seitenhalbierende gegeben. |
Beim Lösen dieser Aufgaben
ist eine Planfigur hilfreich. Das soll an der letzten Aufgabe gezeigt
werden.
...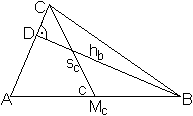 ... ... |
Gegeben sind also die Seite c, die Höhe hb
und die Seitenhalbierende sc.
Das ist der Lösungsweg.
Man zeichnet zuerst das rechtwinklige Dreieck ABD, sucht
den Mittelpunkt Mc der Seite c und erhält den Punkt C über
einen Kreis mit dem Radius sc um Mc. |
Aufgaben dieser Art können sehr anspruchsvoll sein.
A. Bogomolny von Cut-The-Knot hat eine Sammlung von Dreieckskonstruktionen
angelegt. Den Link auf die Seite The many ways to construct a triangle
findet man unten.
Außerhalb
des Dreiecks
top
Außenwinkel
...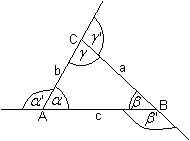 ... ... |
Verlängert man wie in der Zeichnung die Seiten,
so entstehen als Nebenwinkel der Innenwinkel drei neue Winkel, die sog.
Außenwinkel.
Man kann leicht nachweisen:
>Jeder Außenwinkel ist die Summe der nicht anliegenden
Innenwinkel.
>Die Summe der Außenwinkel ist 360°. |
Es gibt sechs Außenwinkel, da zu jedem Innenwinkel
zwei Außenwinkel gehören.
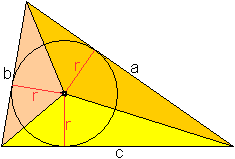
Ankreise
...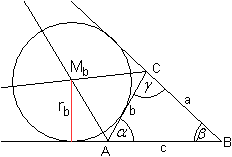 ... ... |
Halbiert man zwei an einer Seite anliegende Außenwinkel,
so schneiden sich die freien Schenkel in einem Punkt, der der Mittelpunkt
eines "Ankreises" ist.
Der Radius des Ankreises, der die Seite b berührt,
ist rb=2A/(a+c-b).
Es gibt zwei weitere Ankreise mit den Radien ra=2A/(b+c-a)
und rc=2A/(a+b-c). |
Beweis
...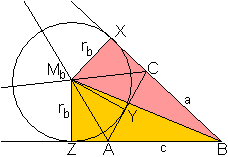 |
Der Flächeninhalt A=A(ABC) des Dreiecks ABC ergibt
sich als
A(ABC)=A(ZBMb)+A(MbBX)-A(MbYCX)-A(ZAYMb). |
...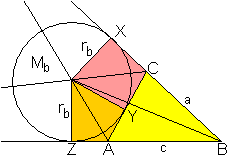 .. .. |
Da die Tangentenabschnitte ZA und AY bzw. YC und CX gleich
sind, ist
A(MbYCX)-A(ZAYMb)=2*A(ACMb).
Dann ist A(ABC)=A(ZBMb)+A(MbBX)-2*A(ACMb)
=(1/2)rb(c+AY)+(1/2)rb(a+CY)-2*(1/2)brb
=(1/2)rbc+(1/2)rba+(1/2)rbc(AY+CY)-2brb=(1/2)rb[c+a+b-2b].
Aus A(ABC)=(1/2)rb[a+c-b] folgt rb=2A/(a+c-b),
wzbw. |
Beziehung
zwischen dem Radius des Inkreises und den Radien der Ankreise
Es gilt 1/r = 1/ra+1/rb+1/rc.
(Algebraischer) Beweis:
1/ra+1/rb+1/rc=(b+c-a)/2A+(a+c-b)/2A+(a+b-c)/2A=(a+b+c)/2A=1/r.
Vom Dreieck zum
Viereck top
...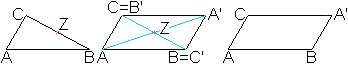 ... ... |
Spiegelt man ein Dreieck an einem Mittelpunkt einer Seite,
entsteht ein Parallelogramm. |
...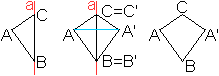 ... ... |
Spiegelt man ein Dreieck an einer Seite, entsteht ein
Drachenviereck. |
Allgemeines
Dreieck im Internet top
Deutsch
Arndt Brünner
Berechnung
von Dreiecken, Herons
Formel für den Flächeninhalt des Dreiecks
Eckard Specht
Klassische
Transversalen
Peter Andree
Die
Beziehung von Stewart und Anwendungen
Wikipedia
Dreieck,
Ausgezeichnete
Punkte im Dreieck, Feuerbachkreis,
Eulergerade,
Höhenfußpunktdreieck,
Kreise
am Dreieck,
Johnson-Kreis,
Dreiecksungleichung,
Satz
von Stewart,
Kimberling-Nummer,
Ankreis,
Kongruenzsätze,
Ähnlichkeitssätze,
Mollweidesche
Formeln, Halbwinkelsatz
Englisch
Clark Kimberling
Encyclopedia
of Triangle Centers (ETC)
A. Bogomolny (Cut-The-Knot)
The many
ways to construct a triangle, Metric
Relations in a Triangle, Triangle
Classification
Eric W. Weisstein (MathWorld)
Triangle,
Medial
Triangle, Herons
Formula,
Triangle
Triangle Picking
Wikipedia
Triangle,
Triangle
center,
Nine-point
circle,
Euler line,
Altitude
(triangle),
Incircle
and excircles of a triangle, Johnson
circles, Triangle
inequality, Stewart's
theorem, Encyclopedia
of Triangle Centers, Incircle
and excircles of a triangle,
Congruence
(geometry), Similarity
(geometry), Mollweide's
formula
Referenzen top
(1) Heinz Nickel (Hrsg.): Algebra und Geometrie für
Ingenieur- und Fachschulen,
Verlag Harry Deutsch, Frankfurt/M und Zürich, 1966
(2) Jan Gullberg: Mathematics- From the Birth of Numbers,
New York, London 1997 (ISBN0-393-04002-X)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2010 Jürgen Köller
top |

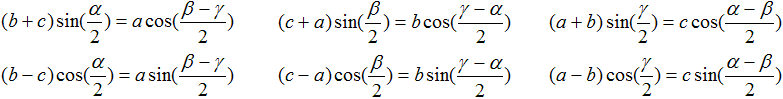
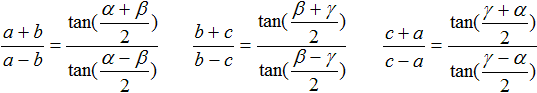
 ...
...


 ...
...

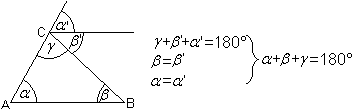 ...
... ...
... ...
...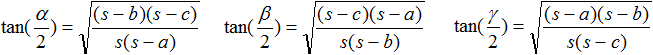




 ...
... ...
... ...
...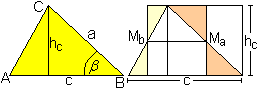 .
. ...
... ...
...



 ...
... ...
...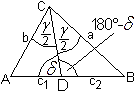 ...
... ...
... ...
... ...
... ....
.... ...
...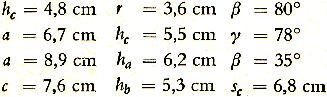 ...
... ...
... ...
... ...
...
 ..
..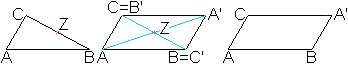 ...
...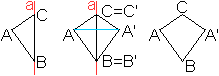 ...
...