|
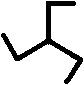
Was ist eine dreistrahlige Figur?
... ... ...
|
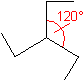
Eine dreistrahlige Figur ist eine drehsymmetrische oder
kreissymmetrische Figur von der Ordnung drei.
Das heißt, dass sie ein Drehzentrum hat und dass
sie bei jeder Dritteldrehung um dieses Zentrum in sich selbst übergeht. |
... ... ...
|
.. ... ... |
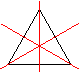
Auch das gleichseitige Dreieck ist dreistrahlig.
Bei ihm kommt noch Achsensymmetrie mit drei Symmetrieachsen
hinzu. |
... ... ...
|
Diese Seite hat den gleichen
Aufbau wie meine Seiten
Vierstrahlige Figuren,
Fünfstrahlige
Figuren, Sechsstrahlige Figuren, Siebenstrahlige
Figuren, Achtstrahlige
Figuren, Neunstrahlige Figuren.
Beispiele
dreistrahliger Figuren top
Gleichseitige Dreiecke
|

Quadrate
|
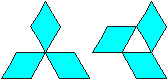
Rauten
|

30-60-90-Dreiecke
|
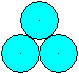
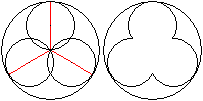
Drei Kreise
|
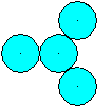
Vier Kreise
|
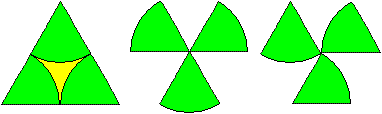
60°-Kreisausschnitte
|
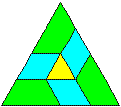
Drei Figuren
|

Vorsicht radioaktiv
|

Kreisverkehr
|

Triskele
|

Dreifachspirale
|

Dreifachknoten
|
|
|
Maßwerk (Dreipass) |
Zykloiden top
Eine Herausforderung liegt darin, dreistrahlige Figuren
mit Hilfe von Formeln zu zeichnen. Da bieten sich die Zykloiden
an.
Epizykloide
...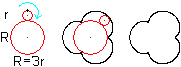 ... ... |
Man stelle sich vor, ein Kreis liege fest und ein zweiter
Kreis mit einem dreimal so kleinen Radius rolle um einen großen Kreis
(Leitkreis) herum. Verfolgt man dabei einen Punkt auf der Kreislinie des
beweglichen Kreises, so beschreibt er eine geschlossene Linie mit drei
Einkerbungen. Diese Linie heißt Zykloide, genauer Epizykloide. Diese
Figur ist dreistrahlig. |
Beschreibt man das Abrollen
durch Formeln, so ergibt sich:
| Epipozykloide, allgemein
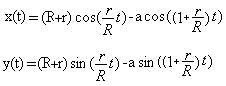
Dabei sind R und r die Radien der Kreise.
|
Epizykloide für R=3r
x(t)=4r*cos(t/3)-a*cos(4t/3)
y(t)=4r*sin(t/3)-a*sin(4t/3)
Oben in der Zeichnung ist a=r. |
Die Variable a gibt die Entfernung des Kurvenpunktes vom
Mittelpunkt des beweglichen Kreises an.
Es folgen Epizykloiden für
r=1 und verschiedene Parameter a.
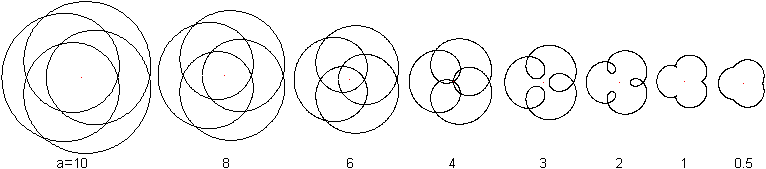 Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
Hypozykloide
....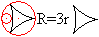 .. .. |
Rollt man den kleinen Kreis innen ab, so entsteht eine
Figur mit drei Spitzen, die Hypozykloide. |
Beschreibt man das Abrollen
durch Formeln, so ergibt sich:
| Hypozykloide, allgemein
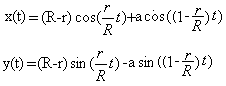
Dabei sind R und r die Radien der Kreise.
|
Hypozykloide für R=3r
x(t)=2r*cos(t/3)+a*cos(2t/3)
y(t)=2r*sin(t/3)-a*sin(2t/3)
Oben in der Zeichnung ist a=r. |
Die Variable a gibt die Entfernung des Kurvenpunktes vom
Mittelpunkt des beweglichen Kreises an.
Es folgen Hypozykloiden für
r=1 und verschiedene Parameter a.
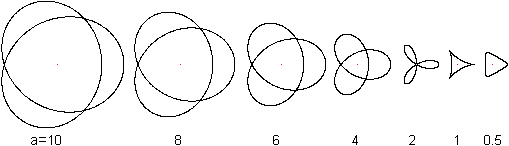 Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
Besondere Zykloiden
top
Von den oben vorgestellten Zykloiden mit R=3r sind drei
hervorzuheben.
Trifolium
(Hypozykloide, a=2r)
...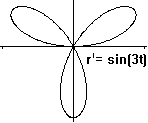 ... ...
|
In Polar-Koordinatensystem hat das Trifolium eine besonders
einfache Darstellung:
r=a*sin(3t) [0<t<2*pi].
Die Länge ist 16,68a und der Flächeninhalt (1/4)*pi*a².
Die Länge kann nur angenähert angegeben werden,
da die Rechnung auf ein elliptisches Integral führt.
Quelle: MathWorld (URL unten) |
Deltoid
(Hypozykloide, a=r)
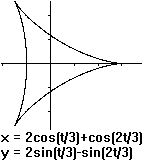
Es gilt 0<t<6*pi.
|
Der Umfang ist 16a und der Flächeninhalt 2*pi*a².
Quelle: (1) Seite 93 |
Dreistrahlige
Epizykloide
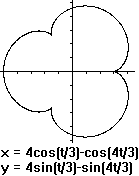
Figuren
aus Gleichungen mit Polarkoordinaten top
Es ist eine schöne Spielerei, die Formel r'=sin(3t)
des Trifoliums z.B.abzuändern und so zu neuen dreistrahligen Figuren
zu gelangen. Es gilt für alle Kurven 0<t<2*pi.
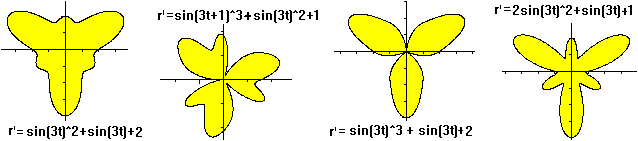
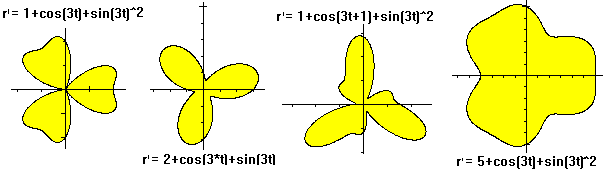 Den linken Graphen unten des Kleeblatts fand ich bei Robert
Ferreol (URL unten)
Den linken Graphen unten des Kleeblatts fand ich bei Robert
Ferreol (URL unten)
Dreistrahlige Körper
top
Zur Definition
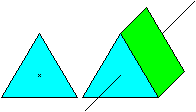 |
Verschiebt man eine Figur in Normalenrichtung, so entsteht
ein Prisma.
Ist die Figur dreistrahlig, so ist auch das Prisma dreistrahlig.
Dabei wird der Drehpunkt durch eine Drehachse ersetzt.
Außerdem hat dieser Körper an Stelle dreier
Symmetrieachsen drei Symmetrieebenen. |
Dreistrahliges
aus der Pflanzenwelt

Horn-Sauerklee,
ein hübsches, aber gefürchtetes Unkraut
|

Schneeglöckchen
|

Buchecker
|
Hasenfenster
in Paderborn
... ... ... |
Das Hasenfenster befindet sich im Kreuzgang des Paderborner
Domes. Es ist das Maßwerk eines gotischen Fensters aus dem 16.Jahrhundert.
"Drei Hasen und der Löffel drei - und dennoch hat
ein jeder zwei"
Das Hasenfenster ist ein Beispiel eines dreistrahligen
Körpers ohne Symmetrieebenen. |
Deckenventilator

|
Dieses Bild wird man in den Tropen immer weniger antreffen.
Die Ventilatoren werden wegen der Klimaanlagen überflüssig. |
Lake
Point Tower in Chicago
... ....
..2005 ....
..2005
|
Informationen über dieses interessante und schöne
Hochhaus findet man u.a. auf der englischsprachigen Wikipedia-Seite "Lake
Point Tower" (URL unten). |
Dreistrahlige
Figuren im Internet top
Deutsch
Claas Hickl
Quattrofolium
(Entdecke die Welt der Kleeblätter)
Wikipedia
Zykloide,
Epizykloiden,
Symmetrie
(Geometrie),
Triskele
Englisch
EricW.Weisstein (MathWorld)
Trifolium,
Hypocycloid
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Rotation,
Rotational
symmetry,
Triquetra,
Triskelion,
Lake
Point Tower
Xah Lee
Deltoid
Französisch
Robert FERRÉOL
DELTOÏDE
Referenzen top
(1) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |
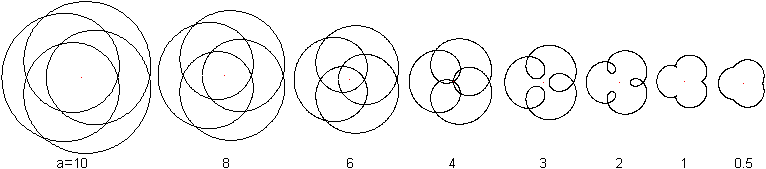
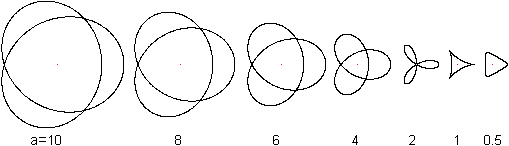
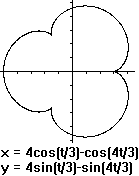
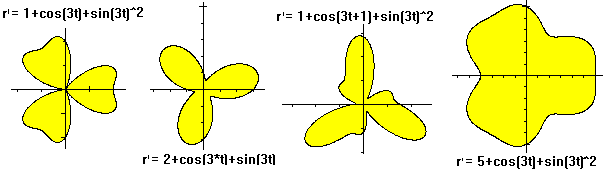
 ...
... ...
... ...
... ...
...













 ...
...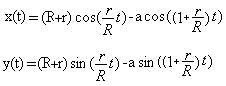
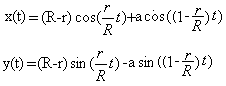
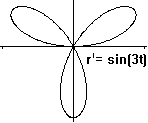 ...
...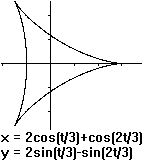
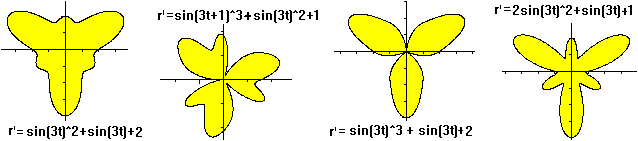




 ...
...
 ....
....
