|
Gleichschenklig-rechtwinkliges
Dreieck
|
Was ist ein gleichschenklig-rechtwinkliges Dreieck?
...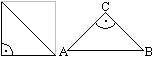 ... ... |
Wenn man ein Quadrat durch eine Diagonale halbiert, entsteht
ein gleichschenklig-rechtwinkliges Dreieck. Es hat somit einen rechten
Winkel und zwei gleich lange Seiten. |
Andere Namen sind 45-90-45-Dreieck oder Halbquadrat.
Wenn auf dieser Seite von einem Dreieck
die Rede ist, dann ist das gleichschenklig-rechtwinklige Dreieck gemeint.
Größen
des Dreiecks top
Größen sind die Hypotenuse AB, die Katheten
AC und BC, die Höhe h, der Flächeninhalt A, der Umfang U, der
Radius R des Umkreises und der Radius r des Inkreises.
Ist z.B. die Hypotenuse a gegeben, so lassen sich die
übrigen Größen berechnen.
...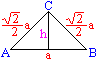 ... ... |
Die Katheten sind gleich sqr(2)/2*a, die Höhe ist
h=a/2.
Die Höhe teilt das Dreieck in wiederum gleichschenklig-rechtwinklige
Dreiecke.
Der Flächeninhalt ist A=a²/4. Der Umfang ist
U=[1+sqr(2)]*a. |
...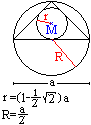 ... ... |
... ... ... |
Ganz links sind der Umkreis und der Inkreis des Dreiecks
eingezeichnet.
Man sieht leicht ein, dass der Umkreis den Radius R=a/2
hat.
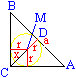
Zur Berechnung des Inkreisradius muss man etwas ausholen:
Es gelten die Beziehungen x=sqr(2)*r und CD=(1/2)a. Weiter
ist CD = x + r.
Setzt man CD und x ein, erhält man (1/2)a
= sqr(2)*r + r.
Der Radius r wird isoliert, der Nenner wird rational
gemacht. Es ergibt sich r=(1/2)[sqrt(2)-1]a.
|
Folgen von Dreiecken
top
...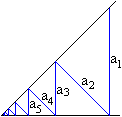 ... ... |
Zeichnet man in den Winkelraum eines 45°-Winkels
eine Zick-Zack-Linie, so entstehen gleichschenklig-rechtwinklige Dreiecke.
Gibt man die vertikale Strecke mit a1=a vor,
so bilden die "Sprossen" die geometrische Folge a1=a, a2=a/sqr(2),
a3=a/[sqr(2)]², a4=a/[sqr(2)]³, ....
Die dazugehörige Summe, also die geometrische Reihe,
hat den Grenzwert [2+sqr(2)]*a. Das ist ungefähr gleich 3,4*a. |
...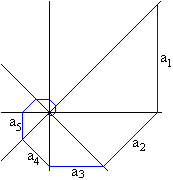 ... ... |
Eine Vertikale, eine Horizontale und die dazugehörigen
Winkelhalbierenden bilden eine Geradenkreuzung aus vier Geraden.
In diese Figur kann man einen Streckenzug einzeichnen,
der die Form einer Spirale hat.
Er wird aus den gleichen Strecken wie die Zickzacklinie
oben gebildet.
Die Länge der Spirale nähert sich wie oben
[2+sqr(2)]*a. |
Körper aus
Dreiecken top
Drei gleichschenklig-rechtwinklige Dreiecke bilden eine
unten offene dreieckige Pyramide. Die Grundfläche ist ein gleichseitiges
Dreieck.
Diese Pyramide kommt in einem Würfel vor, wie das
folgende Stereobild zeigt. Das Bild zeigt zwei Pyramiden dieser Art.
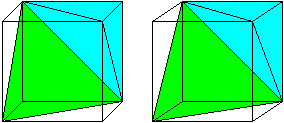
Klappt man die grüne Pyramide nach oben und legt
sie auf die blaue Pyramide (gleichseitiges Dreieck auf gleichseitiges Dreieck),
so erhält man eine Doppelpyramide. Dieser Körper wird von sechs
gleichschenklig-rechtwinkligen Dreiecken begrenzt.
Tangram-Puzzles
top
Klassisches Tangram
...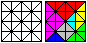 ... ... |
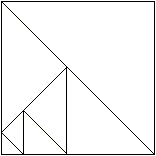
Teilt man ein Quadrat in 16 Quadrate und zeichnet die
Diagonalen ein, so entstehen 32 gleichschenklig-rechtwinklige Dreiecke.
Bestimmte Dreiecke fasst man zu den sieben "Tangramstücken"
zusammen. |
... ... ... |
Aufgabe ist es, aus diesen "Steinen" neue Figuren zu legen.
Mehr findet man auf meiner Tangram-Seite an anderer
Stelle.
Oktagram
...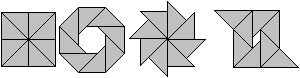 ... ... |
Zeichnet man in ein Quadrat die Diagonalen und die Mittellinien
ein, so entstehen acht gleichschenklig-rechtwinklige Dreiecke. Aus ihnen
kann man neue Figuren legen.
Dieses Puzzle heißt Oktagram (6). |
Quadrat
aus 7 Dreiecken
 Quelle: Ivan Skvarca, Journal of Recreational Mathematics
1998, zugesandt von Wolfgang Schlüter
Quelle: Ivan Skvarca, Journal of Recreational Mathematics
1998, zugesandt von Wolfgang Schlüter
Farbquadrate
top
...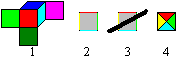 ... ... |
Ein attraktiver Gegenstand für Spielereien ist der
Satz Farbwürfel von Mac Mahon. Das sind
die Würfel, die auf den Seitenflächen sechs verschiedene Farben
in allen Kombinationen haben. Links ist ein Würfel dargestellt. Will
man vom Würfel auf Quadrate zurückgehen, müsste man konsequenterweise
den Quadratseiten vier Farben geben (2). Diese Färbung erweitert man
besser auf die gleichschenklig-rechtwinkligen Dreiecke, die den Seiten
anliegen (3, 4). |
... ... ... |
Es gibt sechs verschiedene Farbquadrate mit vier verschiedenen
Farben. |
...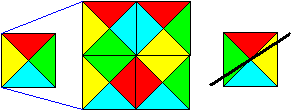 ... ... |
Das Würfelproblem von Mac Mahon lautet für
Quadrate:
Man greife ein Quadrat heraus und baue aus vier der fünf
übrigen Quadrate ein doppelt so großes Quadrat mit gleichen
Farben außen. Innen sollen gleiche Farben aufeinander treffen.
Links wird eine Lösung dargestellt. Das Spiegelquadrat
zum ersten Quadrat bleibt zurück.
|
Diese Farbquadrate heißen auch
Wang-Täfelchen, denn Hao Wang hat für sie 1961 das Parkettierungsproblem
in vielen Variationen erfunden: Man soll die Steine in der Ebene so verlegen,
dass immer gleiche Farben aneinander stoßen. Mehr findet man in Buch
4.
Geodreieck
top
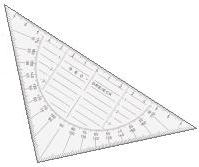 Das Geodreieck ist ein Zeichengerät, das erst in den
1950iger Jahren auf dem Markt kam und sich seitdem immer mehr ausbreitete.
Heute (2003) ist es das Standard-Zeichengerät. Seine Verbreitung
spiegelt eine Entwicklung der Schulgeometrie wider. Ich werde hier aus
meiner (ungenauen) Erinnerung heraus die Entwicklung wiedergeben, die sich
auf das Gymnasium beschränkt.
Das Geodreieck ist ein Zeichengerät, das erst in den
1950iger Jahren auf dem Markt kam und sich seitdem immer mehr ausbreitete.
Heute (2003) ist es das Standard-Zeichengerät. Seine Verbreitung
spiegelt eine Entwicklung der Schulgeometrie wider. Ich werde hier aus
meiner (ungenauen) Erinnerung heraus die Entwicklung wiedergeben, die sich
auf das Gymnasium beschränkt.
Anfang der 1950iger Jahre bereiste ein Vertreter aus Hannover
die Volksschulen um ein neues Zeichengerät anzupreisen. Er wies auf
die folgenden Fähigkeiten hin: Man kann bequem >>Strecken halbieren,
>>Senkrechte und Parallelen zeichnen, >>Winkel zeichnen. Man sparte andere
Zeichendreiecke ein und m.E.auch den Zirkel. Das Geodreieck war allerdings
anfangs ziemlich teuer. Er legte eine Referenzliste von Schulen vor, die
das Dreieck schon eingeführt hatten. Darunter waren viele Berufsschulen.
Für das Gymnasium war das Geodreieck eigentlich überflüssig,
da im Unterricht (der Euklidischen Geometrie folgend) nur konstruiert,
also mit Zirkel und Lineal gezeichnet wurde. Doch die Schüler fanden
schnell heraus, dass das Konstruieren umständlich war und das Zeichnen
mit dem Geodreieck fixer ging. So benutzten sie es heimlich beim Anfertigen
von Hausaufgaben.
Erst als später in den Klassen 5 und 6 vermehrt
Geometrieunterricht vorgeschrieben wurde und das Geodreieck in jeder Familie
vorhanden war, gaben auch die Puristen unter den Lehrern nach. Das Geodreieck
wurde als Zeichengerät des Gymnasiums toleriert und später eingeführt.
Es wurde jedoch von Lehrerseite immer wieder betont, dass das Zeichnen
mit dem Geodreieck nur ein Ersatz für das Kontruieren war.
Die Konstruktion als geometrisches Problem ist inzwischen
fast eine Randerscheinung im Geometrieunterricht geworden und auf
die Zeichnungen beschränkt, die mit dem Geodreieck nicht möglich
sind.
Ich sehe in der Rückschau eine ähnliche Entwicklung
bei der Ablösung des Rechenstabes durch den Taschenrechner in den
1970iger Jahren im Bereich des Zahlenrechnens.
Etwas Nostalgie: Ein Zirkel mit einem
Bleistiftstummel (MADE IN ENGLAND, Pat.1261866&1526566)

Wer kennt ihn noch?
Polyabolos
Mit Figuren aus mehreren gleichschenklig-rechtwinkligen
Dreiecken kann man in Analogie zu den Pentominos
oder den
Polyiamonds viele Lege-Probleme untersuchen.
Sie heißen Polyabolos. Die Tetrabolos aus vier Dreiecken sind der
Favorit, denn die Anzahl 14 der Steine ist nicht zu groß und nicht
zu klein. Weitere Informationen finden sich auf der Seite Polyabolos
an anderer Stelle meiner Homepage.
Auch auf anderen Seiten meiner
Homepage tauchen gleichschenklig-rechtwinklige Dreiecke auf, z.B. beim
Fröbelstern
oder bei Himmel und Hölle.
Gleichschenklig-rechtwinkliges
Dreieck im Internet top
Deutsch
Bildungsserver Südtirol
Messen
von Winkeln mit dem Geodreieck
Wikipedia
Gleichschenklige
Dreiecke, Geodreieck
Englisch
Eric W. Weisstein (MathWorld)
Isosceles
Right Triangle, Polyabolo
Wikipedia Special
right triangles#45-45-90 Triangle, Polyabolo
Referenzen top
(1) Martin Gardner: Mathematische Hexereien, Ullstein,
Berlin/Frankfurt/Wien, 1988 (ISBN 3 550065787)
(2) bild der wissenschaft 8/1979, (Halbquadrat-Mehrlinge),
Seite 102ff.
(3) Karl-Heinz Koch: ...lege Spiele, DuMont, Köln
1987 (ISBN 3-7701-2097-3)
(4) Friedrich L. Bauer: Einladung zur Mathematik, Deutsches
Museum, München 1999
(5) Bruno Kerst: Mathematische Spiele, Berlin 1933 (Nachdruck:
Martin Sändig, Wiesbaden 1968)
(6) Ulrich Namisloh: Oktagram - Grafisches Figurenrätsel
und Legespiel, Köln 1984 (ISBN 3-7701-1636-4)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |



 ...
... ...
...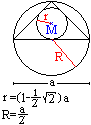 ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
...