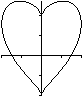|
Was ist die Herzkurve?
 |
Die Herzkurve ist eine in sich geschlossene Kurve, die
die Form des Herzens hat.
Die Herzfom ist als Spielkartenfarbe neben Pik, Kreuz
und Karo wohlbekannt. |
Wenn man von einem Herzen redet, meint man mehr die Herzfläche
als die Herzkurve.
... ... ... |
Im einfachsten Falle besteht ein Herz aus einem auf der
Spitze stehenden Quadrat und zwei auf die Seiten gesetzten Halbkreisen.
Kennzeichen der Herzfigur sind offenbar eine Einkerbung oben und eine Spitze
unten. |
... ... ... |
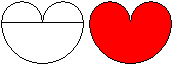
Eine Herzfigur entsteht auch, wenn man auf ein Dreieck
zwei Halbkreise setzt. Dann entstehen seitlich zwei unschöne Ecken.
Man erwartet offenbar, dass die Seiten abgerundet sind. |
... ... ...
|
Fehlt die Spitze unten, so spricht man eher von einer
herzförmigen Figur. Allerdings kommt diese Form dem menschlichen Herzen
näher.
Die Figur besteht aus drei Halbkreisen. |
Gezeichnete Herzkurventop
Methode 1
...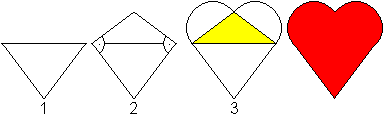 ... ...
|
1 Zeichne ein gleichschenkliges Dreieck.
2 Zeichne zu den Schenkeln die Senkrechten.
Sie erzeugen ein zweites gleichschenkliges
Dreieck.
3 Zeichne über die Schenkel des gelben Dreiecks
Halbkreise. |
Ist das Dreieck unten gleichschenklig-rechtwinklig, so besteht
die Herzkurve wie oben aus einem Quadrat und zwei Halbkreisen.
Methode
2
...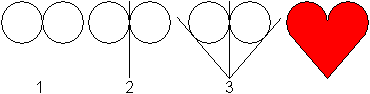 ... ...
|
1 Zeichne zwei sich berührende Kreise.
2 Zeichne die gemeinsame Tangente.
3 Zeichne von einem Punkt der Tangente aus zwei weitere
(äußere) Tangenten. |
Ist der Winkel unten an der Spitze ein rechter, so besteht
die Herzkurve wie oben aus einem Quadrat und zwei Halbkreisen..
Methode
3
...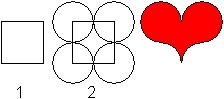 ... ... |
1 Zeichne ein Quadrat.
2 Zeichne gleiche Kreise um die Eckpunkte des Quadrates
mit dem Radius "halbe Quadratseite". |
Methode
4
...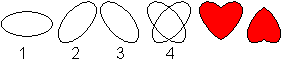 ... ... |
1 Zeichne eine Ellipse.
2 Drehe sie.
3 Spiegele sie.
4 Bilde zwei Herzen. |
Methode
5
...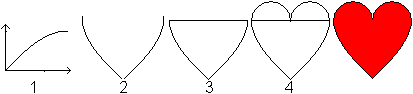 ... ... |
1 Zeichne den Graphen zu f(x)=sin(x), 0<x<pi/2.
2 Drehe die Kurve um 90°. Spiegele diese Kurve.
3 Bilde aus den beiden Kurvenstücken und einer Strecke
ein Dreieck.
4 Setze auf das Dreieck zwei Halbkreise. |
Methode
6
...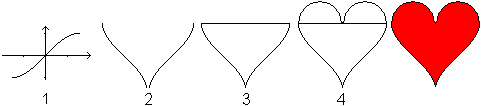 ... ... |
1 Zeichne den Graphen zu f(x)=sin(x), -pi/2<x<pi/2.
2 Drehe die Kurve um 90°. Spiegele diese Kurve.
3 Bilde aus den beiden Kurvenstücken und einer Strecke
ein Dreieck.
4 Setze auf das Dreieck zwei Halbkreise. |
Bézierkurven top
Es gibt die Möglichkeit beliebige Kurven in Grafikprogrammen
zu zeichen, warum nicht auch Herzkurven?
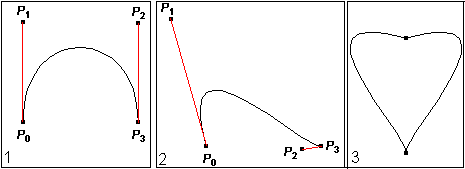 |
1 P0, P1,P2 und P3
stehen
als Kontrollpunkte zur Verfügung. Dabei sind P0 der
Anfangs- und P3 der Endpunkt eines Bogens. P0P1
und P3P2 sind Tangenten an die Kurve.
2 Verschiebe P1 und P2, so dass
sich ein halbes Herz bildet.
3 Ergänze die Kurve nach Drehung und Spiegelung
zu einer Herzkurve. |
Ich verwendete ein Java-Applet einer Seite von Jan Schormann
(URL unten)
Jeder, der das Betriebssystem
Windows verwendet, hat auch das Zeichenprogramm PAINT.
Es wird bei neueren Versionen unter Start/Programme/Zubehör
versteckt. Es hat auch eine Routine für das Kurvenzeichnen.
...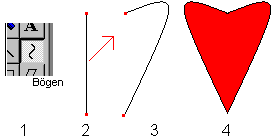 ... ... |
Wähle in der Werkzeugleiste die Schaltfläche
Bögen.
1 Zeichne den Anfangs- und Endpunkt eines Bogens.
2, 3 Fasse mit dem Mauszeiger die Strecke und gehe mit
gedrückter Maustaste in Pfeilrichtung. Fixiere den Bogen mit Klick.
4 Spiegele die Kurve 3 und setze beide Bögen zu
einer Herzkurve zusammen. |
Berechnete
Herzkurven top
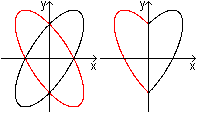
Formeln zu finden, die zu einer
Herzkurve führen, ist eine Herausforderung.
... ... ...
|
Man kann die Methode 4 von oben durch Formeln beschreiben.
Die schwarze Ellipse hat die Formel 2x²-2xy+y²-1=0.
Als Nebenbedingung muss x>=0 sein. Die rote Ellipse hat die Formel 2x²+2xy+y²-1=0.
Als Nebenbedingung muss x<=0 sein. |
Die Einschränkung des Definitionsbereichs kann man weglassen,
wenn man y eliminiert und die Betragsfunktion einsetzt.
Dann stellen y=|x|+sqrt(1-x²) und y=|x|-sqrt(1-x²)
ein Herz dar.[Siehe auch (7)]
Die Spitze unten bekommt
einen Dreh, wenn man die Formeln etwas abändert: y=sqr(|x|)+sqrt(1-x²)
/\ y=sqrt(|x|)-sqrt(1-x²).
Weitere Gleichungen:
Quellen:
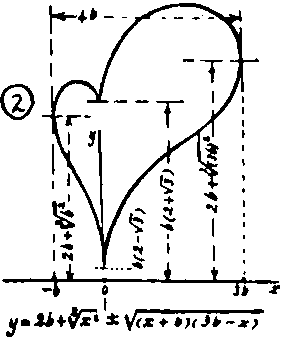
(Bild 1) Buch 8, Eugen Beutel 1901 (2)
Buch 4, Aufgabe 8.5.5.,
(3) nach MathWorld (URL unten) (4)
Webseite von H.-J. Caspar (URL unten) (6) Jurjen N.E. Bos
Aus der Werkstatt von Torsten Sillke
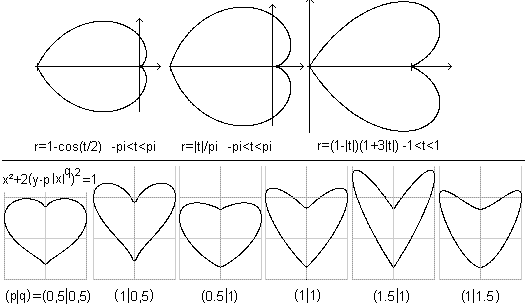
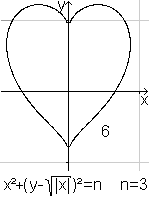
Dreidimensional
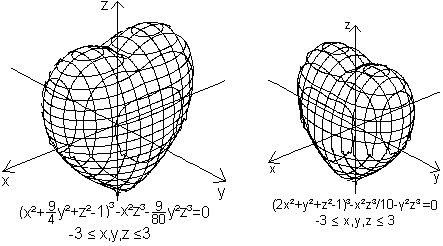
Setzt man y=0 bzw. x=0, so erhält man die Gleichung
des linken 2D-Herzens oben.
gefunden bei MathWorld (URL unten)
Die Graphen wurden erstellt
mit dem Freeware-Programm "winplot" (Version vom 23.05.2000, URL unten).
Winword-Herzen top
Und wie stellen sich Graphiker eine Herzkurve vor?
Das Herz erscheint als bekannte Figur auch in Zeichensätzen
von Programmen unter Windows.
|
Hier eine Auswahl aus bekannten Zeichensätzen. |
Die Zeichensätze sind Normaler Text, Arial, Courier
New, Estrangelo Edessa, Lucida Console, Symbol, Times New Roman, Webdings.
Erst bei einer Vergrößerung der Schrift von
12 auf 72 sieht man die Formen deutlicher.

Die an sich schwarzen Figuren wurden hier mit der Herzfarbe
Rot gefärbt.
Der obere Teil der Herzfigur wird von Kurven ähnlich
den Halbkreisbögen gebildet. Die Linien unten laufen nicht linear
auf die Spitze zu, sondern sind meist erst nach innen und dann nach außen
gebogen. Das verleiht den Herzfiguren einen gewissen Schwung.
Gefunden unter Unicode Standard,
Version 4.0
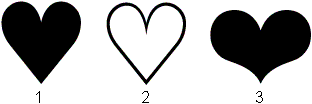
|
1 BLACK HEART SUIT 2665
2 WHITE HEART SUIT 2664
3 HEAVY BLACK HEART 2764 |
Schülerherzentop
Und wie zeichnen heute Schülerinnen und Schüler
spontan ein Herz?
23 Schülerinnen und Schüler der HS Lohfeld
in Bad Salzuflen erhielten die Aufgabe, ein einfaches Herz zu zeichnen.

Dank an die Klasse 7c, Jg.2003/2004, etwa 12 Jahre alt.
Kardioide top
Entstehung
... ... ... |
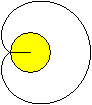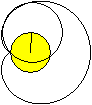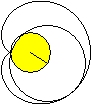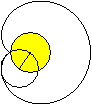
Man gibt einen festen Kreis (links, gelb) vor und rollt
einen gleich großen Kreis auf ihm ab.
Markiert man auf der Kreislinie des beweglichen Kreises
einen Punkt und verfolgt während eines Umlaufs den Weg dieses Punktes,
so beschreibt er die Herzkurve oder
Kardioide (rechts). |
...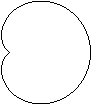 ... ... |
Zweite
mögliche Entstehung
... ... ... |
Eine Kardiode entsteht auch als Einhüllende von
Kreisen.
Gegeben ist ein (gelber) Kreis und ein Punkt P der Kreislinie.
Alle Kreise, deren Mittelpunkte auf der Kreislinie des
(gelben) Kreises liegen und die durch den festen Punkt P gehen, haben als
Einhüllende eine Kardioide. |
Flächeninhalt
und Umfang der Kardioide
Man verwendet zur Berechnung der beiden Größen
A und U am besten die einfachste Darstellung der Kardiode, nämlich
die Polarform r=2a[1+cos (phi)]. Für diese einfache Gleichung liegt
der Nullpunkt des Koordinatensystems in der Spitze der Kardioide.
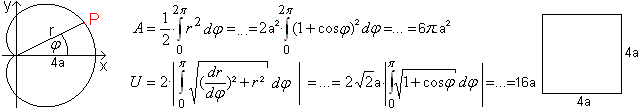 Der Umfang ist rational und so groß wie der Umfang
eines Quadrats mit der Seite 4a.
Der Umfang ist rational und so groß wie der Umfang
eines Quadrats mit der Seite 4a.
Apfelmännchen
und Kardioide
...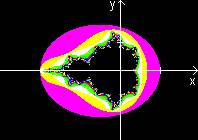 ... ... |
Der "Hauptkörper" der Mandelbrotmenge hat die Form
einer Kardioide. Der zweite Name Apfelmännchen greift diese
Form auf.
Der Hauptkörper hat nicht nur die Form, er ist eine
Kardioide. Die Punkte der Mandelbrotmenge, denen eine konvergente Folge
zuzuordenen ist, bilden das Innere einer Kardioide.
Quelle: (5), Seite 208ff. Dort finden sich auch ein Beweis
und Literaturangaben. |
Das Bild stammt von meiner Seite Apfelmännchen.
Katakaustik
und Kardioide
... ... ... |
Fällt Licht auf einen sphärischen Spiegel (Trauring
im Sonnenlicht), so bildet das reflektierte Licht eine Brennfläche,
die Katakaustik. Das ist aber keine Kardioide, sondern eine sogenannte
Nephroide.
Eine Kardioide entsteht als Einhüllende, wenn Lichtstrahlen
von einem Punkt eines Kreises ausgehen und dann innen an der Kreislinie
reflektiert werden (rechts). |
...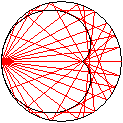 |
Das Foto stammt von meiner Seite Ringe.
Richtcharakteristik
eines Mikrofons
...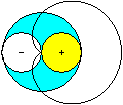 ... ... |
Mikrofone besitzen eine bestimmte Richtcharakteristik.
Bei Schalldruckempfänger ist sie kugelförmig, bei Druckgradientenempfängern
(Schnelleempfängern) ist sie keulenförmig und ähnelt einer
liegenden Acht.
Bestimmte Mikrofone wie Kondensatormikrofone haben beide
Eigenschaften. Ihre Richtcharakteristik entsteht durch Überlagerung
und führt zu einer Kardioide. |
Quelle: (6), Seite 550
Das gebrochene Herz
top
Das gebrochene Herz ist ein Tangramspiel.
...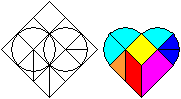 ... ... |
Man legt in ein 3x3-Quadrat zwei Kreise und verbindet
gewisse Punkte. Auf diese Weise entsteht ein Herz, das in neun Stücke
aufgeteilt wird. |
...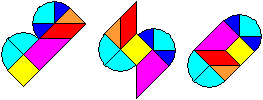 ... ... |
Aufgabe ist es, aus den Stücken
wieder das Herz zu legen oder neue Figuren zu entdecken.
Quelle: (1) Seite 22, (2) Seite 140-145
Das geflochtene
Herz top
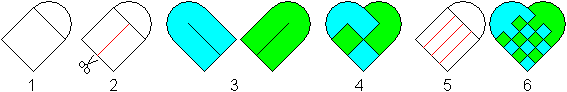
1 Zeichne ein Quadrat mit aufgesetztem Halbkreis.
2 Schneide längs der roten Linie. - Stelle
ein zweite Figur, eine Kopie, her.
3 Färbe die Blätter in zwei verschiedenen Farben
oder verwende gleich Buntpapier.
4 Stecke die beiden Figuren ineinander.
5,6 Das Herz wird ansehnlicher, wenn man mehr Streifen
verwendet.
... ... ...
|
Wer möchte, kann auch die Seite Herzkörbchen
besuchen, die mir Christopher Hamkins zur Verfügung gestellt hat. |
Origami-Herz
top
... ... ... |
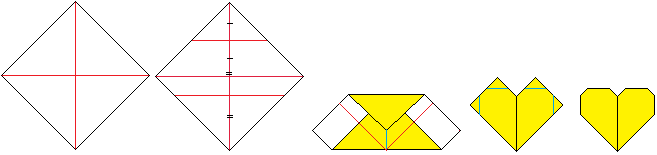 |
Parkettierung
mit Herzen top
...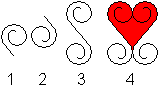 ... ... |
1 Gib eine Spirale vor.
2 Spiegele die Spirale an ihrem Endpunkt.
3 Setze die beiden Spiralen zu einer Doppelspirale zusammen.
4 Spiegele die Doppelspirale. Sie bildet mit dem Urbild
ein Herz. - Viele Herzen führen zu einer Parkettierung (rechts). |
...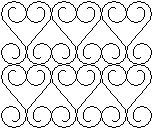 ... ... |
Die Idee zu diesem Entwurf stammt von einem Fenstergitter
in Venedig (Juni 2004).

Venedig ist reich an Gittern
mit Herzen.

Venedig ist exemplarisch
für Herzgitter. Man findet auf meiner Seite Spiralen
ein weiteres Foto aus den USA.
Rosetten aus
Herzfiguren top
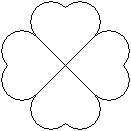
Glückskleeblatt
|

Noch einmal ein Foto aus Venedig - mit etwas Rot nachgeholfen
|
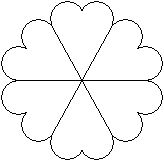
Sechs Waffeln
|

|
Ein Schwanenpaar bei der Balz |
Foto dazu bei der fotocommunity (URL unten)
Emoticons top

Referenzen top
(1) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1998 ISBN 3-88034-87-0]
(2) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont
taschenbuch1480) [ISBN 3-7701-2097-3]
(3) Heinz Nickel u.a: Algebra und Geometrie für Ingenieur-
und Fachschulen, Frankfurt / Zürich 1966
(4) Hans Schupp, Heinz Dabrock: Höhere Kurven,
BI Wissenschaftsverlag 1995 [ISBN 3-411-17221-5]
x^2 + 2( 3/5 (x^2)^(1/3) - y )^2
= 1
(5) Herbert Zeitler: Über die Hauptkörper spezieller
Funktionen, MNU, Jg.52, 1999, Heft4
(6) Bergmann-Schaefer: Lehrbuch der Expermentalphysik,
Berlin, NewYork 1975 [ISBN 3 11 004861 2]
(7) Norbert Herrmann: Mathematik ist überall, Oldenbourg
Verlag 2004 [ISBN 3-486-57583-X]
y = |x| +- sqrt(1 - x^2)
y = 2/3 ( (x^2 + |x| - 6)/(x^2
+ |x| + 2) +- sqrt(36 - x^2) ) (siehe auch Webseite von Thomas Jahre)
(8) Eugen Beutel: Algebraische Kurven, G.J. Göschen,
Leipzig 1909-11
(x^2 + y^2 - 1)^3 = 4x^2*y^3
(9) Ulrich Graf: Kabarett der Mathematik, Dresden,
L. Ehlermann, 1942 Hardcover, 1.Auflage. (1943 Hardcover. 2. Auflage.)
y = 2/3 ( (x^2 + |x|
- 6)/(x^2 + |x| + 2) +- sqrt(36 - x^2) ).
(10) Michael Zettler: Und noch ein Herz. PM 6/99 Seite
274
y = sqrt(1 - (|x|-1)^2),
y = arccos(1 - |x|) - pi
(11) Thomas Hechinger: ... und noch ein weiteres
Herz. PM 2/00 Seite 67
y = sqrt(1 - (|x|-1)^2),
y = -3 sqrt(1 - sqrt(|x|/2))
(12) Mitteilung von Torsten Sillke:
x^2 + 2 (y - p*|x|^q)^2 = 1 (siehe
Schupp / Eisemann)
r = 2 sin^2(phi/4) = 1 - cos(phi/2)
mit |phi| <= pi (siehe Eisemann)
r = |phi|/pi
mit |phi| <= pi. (Archimedische Spirale)
r = (1 - |phi|)(1 + 3|phi|)
mit |phi| <= 1. (siehe Caspar)
(13) El-Milick, Elements d'Algebre
Ornementale, Paris, 1936:
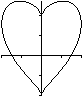
y=(x)^(2/3)+(a²-x²)^(1/2)
und y=x^(2/3)-(a²-x²)^(1/2) und a=2
|
|
Die Herzkurve im
Internet top
Deutsch
33. Evangelischer Kirchentag in Dresden 2011
Google
Bilder
Armin Dietz
Das Herzsymbol
Christian Ucke und Christian Engelhardt
Kaustik
in der Kaffeetasse
[erschienen in: Physik in unserer Zeit, 29 (1998), Seite
120 bis 122]
luther.de
Die
Lutherrose
Fotocommunity
Frühlingsgefühle
(Thomas Th.)
Benutzer:Georg-Johann (Wikipedia)
Von
Punkt zu Punkt |
x(t)=12sin(t)-4sin(3t)
y(t)=13cos(t)-5cos(2t)-2cos(3t)-cos(4t) |
 |
Hans-Jürgen (Matroids Matheplanet)
Herzkurven
Hans-Jürgen Caspar
Kurven
x = a (-phi² + 40 phi +1200)
sin(pi*phi/180)
y = a (-phi² + 40 phi +1200)
cos(pi*phi/180)
Friedrich Krause
y = sqrt(|x|) +- sqrt(1 - x^2)
Michael Holzapfel
Herzkurve
aus zwei Funktionsteilen
y = sqrt(1 - (|x|-1)^2),
y = arccos(1 - |x|) - pi
(x^2 + y^2)(x^2 + y^2 - 2ax) -
a^2y^2 = 0 (Kardioide)
NN (Matheplanet)
Geometrie
in der Teetasse
Thomas Jahre (Chemnitzer Schulmodell)
Ein Herz für die Mathematik |
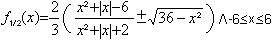 |
Torsten Sillke
Herzkurven
Wikipedia
Kardioide,
Herz
(Symbol), Herz
(Heraldik),
Herz
(Farbe)
Englisch
Alex Bogomolny (Cut The Knot!)
Hearty
Munching on Cardioids
Eric W. Weisstein (MathWorld)
Circle
Catacaustic
Jan Wassenaar
cardioid
JOC/EFR (School of Mathematics and Statistics, University
of St Andrews, Scotland)
Cardioid
Kurt Eisemann
x^2 + (y - 3/4 (x^2)^(1/3))^2 =
1 (Footnote)
r = sin^2( pi/8 - phi/4 ) (Footnote)
pacifict.com
Heart(3D)
Pavel Boytchev
Mathematics
... loves you (Video)
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Cardioid,
Heart
(symbol)
Xah Lee
Cardioid
Französisch
Robert FERRÉOL (mathcurve)
CARDIOIDE,
DOUBLE-COEUR
Japanisch
Nobuo YAMAMOTO
Heart
Curves, Heart
Curves II , Heart
Curves IIb
Ich bedanke mich bei Torsten
Sillke für etliche Tipps.
Im Internet gefunden ;-):
------------------------------
the nerdy way of drawing a heart.
http://www.mathematische-basteleien.de/heart.htm
Must they do EVERYTHING in math? ><;; lol.
------------------------------
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
Jürgen Köller 2004
top |
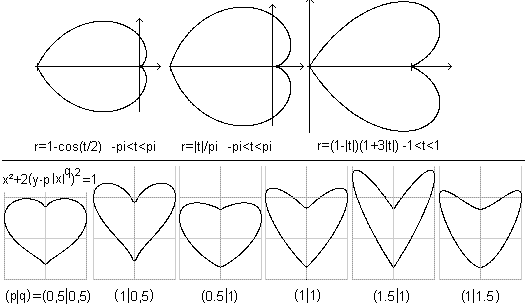
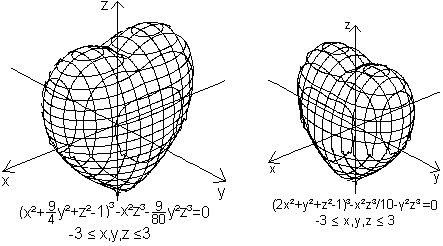

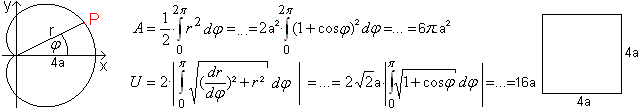


 ...
... ...
... ...
...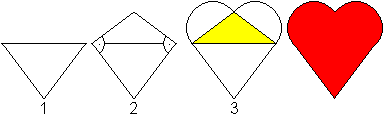 ...
...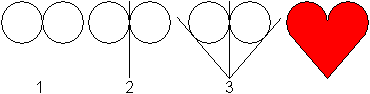 ...
... ...
...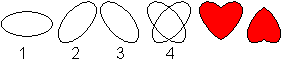 ...
... ...
... ...
...
 ...
... ...
...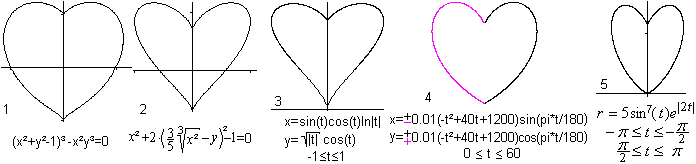

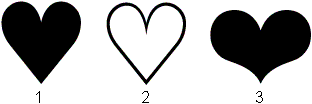
 ...
... ...
... ...
... ...
... ...
...
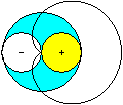 ...
...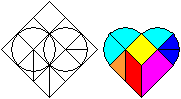 ...
...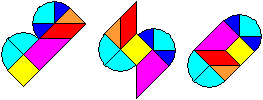 ...
...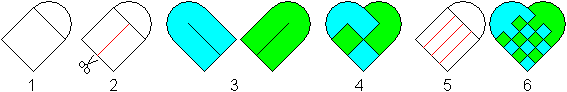
 ...
... ...
...
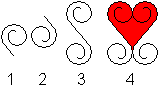 ...
... ...
...