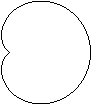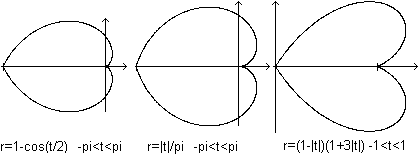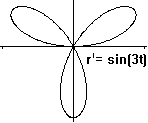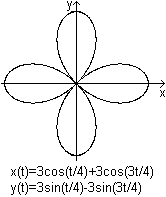|
Kurven im Polarkoordinatensystem
|
Was sind Kurven im Polarkoordinatensystem?
Kurven erhält man meist mit Hilfe von Gleichungen,
die Beziehungen zwischen Koordinaten beschreiben.
...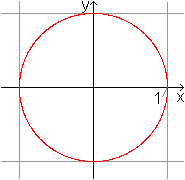 .... .... |
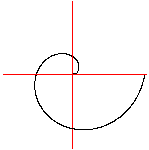
Man erhält zum Beispiel einen Kreis mit dem Radius
R, wenn man im kartesischen Koordinatensystem den Graphen zur Relation
x²+y²=R²
bestimmt. |
...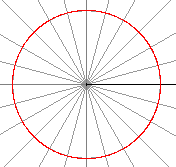 ... ... |
Der Kreis gehört zu den Kurven, die sich im sogenannten
Polarkoordinatensystem bequemer beschreiben lassen.
Es gilt für den Kreis r(t)=R. |
Auf dieser Seite sollen Polarkoordinaten eingeführt
und auf die Darstellung von Kurven angewandt werden.
Einführung
des Polarkoordinatensystems top
Kartesische Koordinaten
...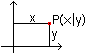 ... ... |
Im kartesischen Koordinatensystem gibt man zwei aufeinander
senkrecht stehende Achsen vor, die sich im Nullpunkt schneiden.
Man legt einen Punkt in der Ebene fest, indem man die
Abstände zu den Achsen und entsprechende Vorzeichen angibt. |
Polarkoordinaten
...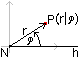 ... ... |
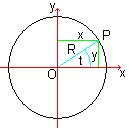
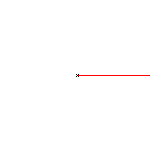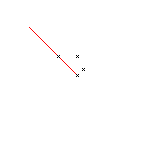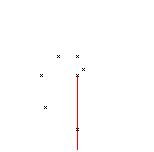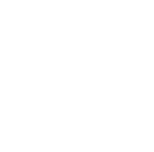
Bei Polarkoordinaten führt man einen (horizontal
liegenden) Strahl h ein, der in einem Nullpunkt N beginnt. Man legt in
der Ebene einen Punkt P fest, indem man ihn mit dem Nullpunkt N verbindet
und dann die Entfernung r vom Nullpunkt und den Winkel phi zwischen der
Geraden NP und der Halbgeraden h angibt.
P(r|phi)
|
Der Winkel wird entgegen dem Uhrzeigersinn orientiert.
Man nennt den Nullpunkt N
auch Pol, die Halbgerade h Polarachse, den Radius r auch Radiusvektor oder
Polabstand und den Winkel phi auch Polarwinkel. (1) Seite 212
Grundmengen
Für das kartesische Koordinatensystem sind die Grundmengen
der x- und y-Werte die Menge der reellen Zahlen.
So einfach ist es hier nicht.
Beim Polarkoordinatensystem darf von der Definition her
der Radius nur positive Zahlen annehmen.
Für die Winkel genügen für die Darstellung
von Punkten der Ebene die Zahlen von Null bis ausschließlich 360°.
Aber es ist zweckmäßig, auch Winkel über
360° zuzulassen. Dann erfasst man zum Beispiel auch die Spiralen. Allerdings
gibt es dann nicht mehr eine eineindeutige Zuordnung zwischen Winkel und
Punkt. Zu jedem Winkel gibt es zwar einen Punkt, aber einem Punkt können
neben phi die Winkel phi+n*360° (n=1,2,3,...) zugeordnet werden.
Bei Verwendung von Polarkoordinaten
bevorzugt man zur Messung des Polarwinkels das Bogenmaß, wobei man
die Einheit rad weglässt wie auch die Längeneinheit beim Radius.
Hier eine Gegenüberstellung der beiden Winkelmaße.
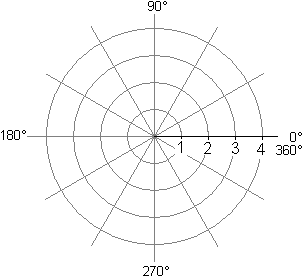
Winkelmaß
|
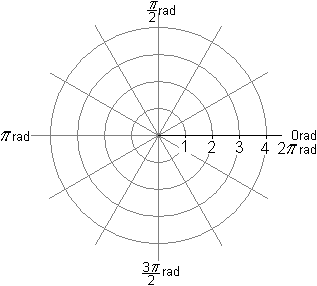
Bogenmaß
|
Beziehungen
... ... ...
|
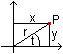
Die Beziehungen zwischen den beiden Koordinatensystemen
wird durch trigonometrische Funktionen vermittelt.
Es gilt cos(t)=x/r und sin(t)=y/r bzw. x=r*cos(t) und
y=r*sin(t).
Dabei wird vorausgesetzt, dass die Nullpunkte zusammenfallen. |
Es folgen Kurven dargestellt
durch Polarkoordinaten.
Entsprechende Darstellungen im kartesischen Koordinatensystem
werden meist weggelassen.
Von jetzt an wird auf dieser
Seite die Winkelbezeichnung phi durch den bequem zu schreibenden Buchstaben
t ersetzt.
Spiralen
durch Polargleichungen
top
Spiralen sind das Paradebeispiel für eine sinnvolle
Verwendung von Polarkoordinaten.
...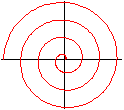 |
Die einfachste Spirale ist die archimedische Spirale
mit r(t)=t.
Es gilt hier |D={t | 0 <= t <= 7*pi}. |
Wie sie entsteht, zeigen
die drei folgenden Bilder.
Der Radius (links) und gleichzeitig der Winkel (Mitte) wachsen
gleichförmig.
Das führt im Zusammenspiel zur Spirale (rechts).
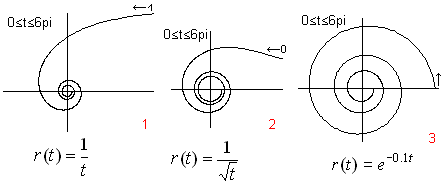
Allgemeiner führt jede Gleichung, in der der Radius
mit dem Winkel steigt oder fällt, zu Spiralen.
Das zeigen die folgenden Beispiele.
Näheres findet man auf meiner Seite Spiralen.
Kreise
durch Polargleichungen
top
... ... ... |
Die bekannte Darstellung eines Kreises mit dem Radius
R ist die Mittelpunktform x²+y² = R² (s.o.).
In Polarkoordinaten ist die einfache Gleichung r(t)=R
dieser Kreis. Bei ihm ändert sich der Radius mit dem Winkel nicht.
Verschiebt man den Mittelpunkt des Kreises vom Nullpunkt
weg, dürfte die Darstellung in Polarform umständlich werden. |
Die Sinus- und Kosinusfunktion
führen auch zu Kreisen.
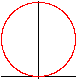
r(t)=sin(t)
|
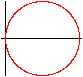
r(t)=cos(t)
|
Nachweis
Für den Kreis zum Sinus gilt:
Mittelpunkt M(0|1/2), Radius 1/2.
Dann gilt x²+(y-1/2)²=(1/2)²
<=> x²+y²-y+1/4=1/4
<=> x²+y²=y
<=> r²=y
<=> r=y/r
<=> r=sin(t).
|
Für den Kreis zum Kosinus gilt:
Mittelpunkt M(1/2|0), Radius 1/2.
Dann gilt (x-1/2)²+y²=(1/2)²
<=> x²-x+1/4+y²=1/4
<=> x²+y²=x
<=> r²=x
<=> r=x/r
<=> r=cos(t).
|
Die Schlussrichtung ist von unten nach oben.
Es fällt auf, das links
der Kreis im ersten und zweiten Quadranten liegt, rechts im ersten und
vierten.
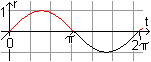
Trägt man die beiden Funktionen in einem kartesischen
Koordinatensystem r gegen t ab, so wird die Lage verständlich.
Ersetzt man in r(t)=sin(t)
bzw. r(t)=cos(t) die Variable t durch t+a, so bedeutet das, dass die Sinus-
bzw. Kosinuskurve längs der t-Achse verschoben wird. Das führt
im Polarkoordinatensystem zu Drehungen des Kreises.
Die Radien bleiben mit r=1/2 erhalten.

r(t)=sin(t)
|
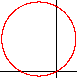
r(t)=sin(t-1/2)
|

r(t)=cos(t)
|
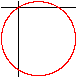
r(t)=cos(t+1)
|
Geraden
durch Polargleichungen
top
Beispiel
...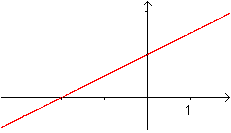 ... ... |
Die Gerade links hat die Darstellung y=(1/2)x+1.
Setzt man x=r*cos(t) und y=r*sin(t), so ergibt sich r*sin(t)=(1/2)r*cos(t)+1
oder r(t)=1/[(sin(t)-(1/2)cos(t)].
Das ist die Geradengleichung in Polarform. |
Verallgemeinerung
Eine Gerade hat die Darstellung y=mx+b. Mit x=r*sin(t)
und y=r*cos(t) ergibt sich die Geradengleichung in Polarform: r(t)=b/[sin(t)-m*cos(t)].
Geraden parallel zur y-Achse haben die Darstellung
x=a. Das führt mit x=r*cos(t) zu r(t)=a/cos(t).
Von den sechs trigonometrischen
Funktonen führen die im deutschsprachigen Bereich weniger bekannten
Sekans- und Kosekansfunktion auch zu Geraden [sec(t)=1/cos(t), csc(t)=1/sin(t)].
Das ist leicht einzusehen: Man setze in r(t)=b/[sin(t)-m*cos(t)]
m=0, b=1 bzw. in r(t)=a/cos(t) a=1.
Weitere Kurven top
Ellipse
...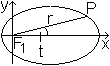 |
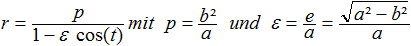 |
Für die Ellipse ist epsilon < 1.
Für die Parabel ist epsilon = 1.
Für die Hyperbel ist epsilon > 1. |
Mehr findet man auf meinen Seiten Ellipse,
Parabel
und Hyperbel.
Herzkurven
Kardioide
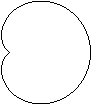
r=2[1+cos(t)]
|
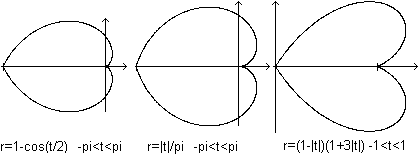
|
Mehr findet man auf meiner Seite Herzkurven.
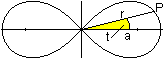
Eine Achtkurve
|
Die Lemniskate wird durch die Polargleichung r(t)=sqrt[cos(2t)]
dargestellt. |
Mehr findet man auf meiner Seite Achtkurven.
Eilinien
Folium
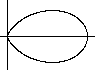
r(t)=cos³t
|
Doppel-Ei
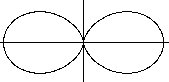
r(t)=cos²t
|
Krummes Ei
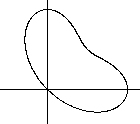
r(t)=sin³t+cos³t
|
Mehr findet man auf meiner Seite Eilinien.
Rosetten
Trifolium
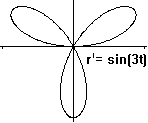
|
Quadrifolium
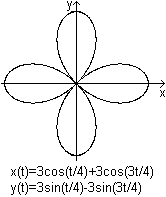
|
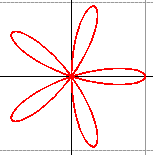
r=sin(5t)
|
Mehr findet man auf meinen Seiten Dreistrahlige
Figuren und Vierstrahlige Figuren.
Noch
weitere Kurven
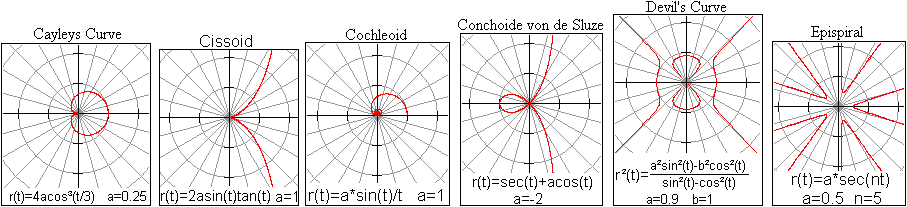
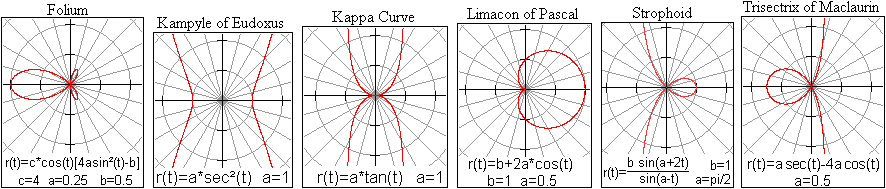
Mehr findet man über diese Kurven in der folgenden
Linkliste.
Kurven
im Polarkoordinatensystem im Internet top
Deutsch
Wikipedia
Polarkoordinaten,
Konchoide,
Konchoide
von de Sluze, Kegelschnitt,
Pascalsche
Schnecke, Strophoide,
Zissoide
Englisch
Abdelkader Dendane
Polar
Coordinates and Equations (Java Applet)
Eric W. Weisstein (MathWorld)
Polar
Coordinates, Polar
Angle,
Cayleys
Sextic,
Cycloid
of Ceva,
Cissoid
of Diocles, Cochleoid,
Conchoid,
Conchoid
of de Sluze, Conchoid
of Nicomedes, Devil's
Curve, Epispiral,
Freeth's
Nephroid, Hippopede,
Kampyle
of Eudoxus, Kappa
Curve, Limaçon,
Maclaurin
Trisectrix, Quadratrix
of Hippias, Rose,
Strophoid,
Tschirnhausen
Cubic, Watt's
Curve
Jan Wassenaar (2dcurves)
Algebraic curves
Cubic: conchoid
of de Sluze, cissoid,
oblique
strophoid,
right
strophoid,
trisectrix
of Longchamps,
trisectrix
of MacLaurin
Quartic: hippopede,
devil's
curve,
kampyle
of Eudoxus,
kappa
curve,
limaçon
sextic: nodal
curve, rhodenea,
arcs
of Samothrace,
Cayley's
sextic, Ceva's
trisectrix, dipole
curve, scarabaeus
Others: generalized
arcs of Samothrace, generalized
bean curve
Richard Parris (Freeware-Programme)
winplot
The MacTutor History of Mathematics archive
Famous
Curves index
Wikipedia (List
of curves)
Polar
coordinate system,
Cardioid,
Cissoid
of Diocles,
Cochleoid,
Conchoid
of de Sluze, Conic
section, Devil's
curve, Epispiral,
Folium
of Descartes, Hippopede,
Kampyle
of Eudoxus,
Kappa
curve, Strophoid,
Trisectrix
of Maclaurin
Xah Lee
A
Visual Dictionary of Special Plane Curves
Französisch
Robert FERRÉOL
COURBES
2D
Referenzen top
(1) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008 Jürgen Köller
top |

 ....
.... ...
... ...
... ...
...

 ...
...
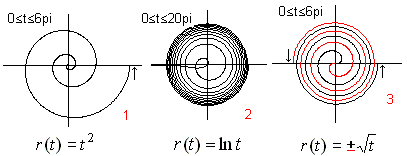
 ...
...




 ...
...