|
Was ist ein Kreis?
...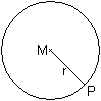 ... ... |
Die Menge aller Punkte P, die von einem festen Punkt
M die gleiche Entfernung r haben, bilden einen Kreis oder genauer eine
Kreislinie mit dem Mittelpunkt M und dem Radius r. |
Ein Kreis kann auch eine Kreisscheibe sein.
Dann ist der Kreis die Menge aller Punkte der Kreislinie
und der Punkte, die sie einschließt.
Auf dieser Seite findet man
eine persönliche Auswahl von "Kreisgeschichten".
Begriffe am Kreis top
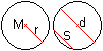 |
M Mittelpunkt,
r Radius oder Halbmesser,
d Durchmesser
s Sehne |
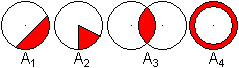 |
A1 Kreissegment oder Kreisabschnitt
A2 Kreisausschnitt oder Kreissektor
A3 Kreislinse
A4 Kreisring |

|
k Kreis oder Kreislinie
b Kreisbogen
alpha Mittelpunktwinkel
beta Umfangswinkel |
|
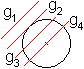
g1 Passante
g2 Tangente
g3 Sekante
g4 Zentrale |
Flächeninhalt
und Umfang top
Ein Kreis ist im Allgemeinen durch den Radius r
gegeben. Dann ist der Flächeninhalt A=pi*r² und
der
Umfang U=2*pi*r.
Dabei ist pi eine transzendente Zahl.
Eine Näherungsangabe auf 30 Dezimalen genau ist
pi=3.141592653589793238462643383279.
Erste
Herleitung mit Hilfe der Integralrechnung
Am einfachsten ist es, die beiden Formeln für den
Flächeninhalt und den Umfang mit Hilfe der Integralrechnung herzuleiten.
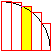
Aus Gründen der Symmetrie genügt es, sich auf
den Viertelkreis zu beschränken.
Seine Funktionsgleichung ist f(x)=sqrt(r²-x²).
... ... ...
|
Zur Herleitung der Formeln zerlegt man den Viertelkreis
in Streifen.
Für den Flächeninhalt summiert man den Flächeninhalt
der Streifen,
für den Umfang die Länge der Sehnen innerhalb
der Streifen. |
Flächeninhalt A
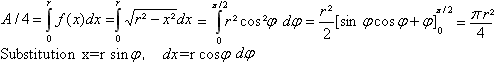
Umfang U
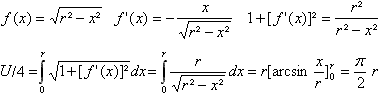
Zweite
Herleitung für den Schulgebrauch
Flächeninhalt
... ... ... |
Steht die Integralrechnung nicht zur Verfügung,
so kann man in einer ersten Überlegung eine Intervallschachtelung
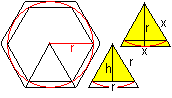
verwenden. Man legt zum Beispiel um den Kreis und in den Kreis ein regelmäßiges
Sechseck. |
Das äußere Sechseck hat ein Grunddreieck mit der
Höhe r und der Seite x mit r=sqrt(3)/2*x oder x=(2/3)sqrt(3)*r. Der
Flächeninhalt ist A1=xr/2=sqrt(3)/3*r².
Das innere Sechseck hat ein Grunddreieck mit der Seite
r und der Höhe h=sqrt(3)/2*r. Der Flächeninhalt ist A2=hr/2=sqrt(3)/4*r².
Das äußere Sechseck hat also einen Flächeninhalt
von 6A1=2sqrt(3)r², das innere 6A2=(3/2)sqrt(3)r².
Der Flächeninhalt des Kreises liegt damit zwischen
2sqrt(3)r² und (3/2)sqrt(3)r² oder 3,46r² und 2,60r².
Der Mittelwert ist 3,03r². Das führt zu pi=3,03.
Die Methode kann man zu einer
echten Intervallschachtelung erweitern, wenn man die Vieleckfolge
Dreieck, Sechseck, Zwölfeck, ...untersucht. Dann kann man pi beliebig
genau bestimmen.
Umfang 1
Mit Hilfe des Sechsecks erhält man die Schranken
6r>U>4sqrt(3) oder 6r>U>6,93r. Das führt zu pi=3,32.
Umfang 2
Für den Umfang gibt es noch eine anschauliche Überlegung.
... |
...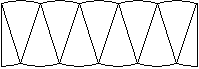 ... ... |
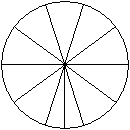
Man zerlegt die Kreisfläche in Kreisausschnitte
und setzt sie zu einer neuen Figur zusammen. Wenn man die Anzahl der Kreisausschnitte
immer größer werden lässt, kann man sich vorstellen, dass
die Figur sich immer mehr der Rechteckform nähert. |
Der Flächeninhalt ist A=r(U/2). Daraus folgt U=2A/r=2*pi*r.
Dritte
(experimentelle) Herleitung
Für den Physikunterricht kommen die Formeln A=pi*r²
und U=2*pi*r in Klasse 10 zu spät. Schon bei Schülerübungen
zur Dichtebestimmung mit Zylindern in Klasse 6 kommt man nicht am Kreis
vorbei.
Man wiegt ein Quadrat aus Pappe mit bekannter Fläche
und schließt dann durch Dreisatzrechnung auf die Masse pro cm².
Man wiegt Kreisscheiben aus der gleichen Pappe und misst
die Radien.
Man rollt die Kreisscheiben ab und gelangt so zum Umfang.
In beiden Fällen kommt man zu Messreihen A=A(r²)
und U=U(r). Der Proportionalitätsfaktor ist pi bzw. 2*pi.
Kreisteile top
Einfache Kreisteile sind der Kreisausschnitt und der
Kreisabschnitt.
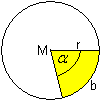
|
Der Kreisausschnitt wird
begrenzt von einem Kreisbogen b und zwei Radien r.
Für den Kreisbogen gilt: b : (2*pi*r)=alpha
:
360°
oder b=(pi*alpha*r)/180°.
Für den Flächeninhalt gilt: A' : (pi*r²)=alpha
:
360°
oder A'=(pi*r²)(alpha)/360°).
|
Der Kreisausschnitt wird
auf meiner Webseite Kreisausschnitt ausführlich
besprochen.
Der Kreisabschnitt
wird von einem Kreisbogen b und einer Sehne s begrenzt. Man erhält
den Flächeninhalt, wenn man die Dreiecksfläche vom Flächeninhalt
des Kreisausschnittes subtrahiert.
...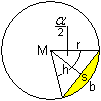 ... ... |
Für die Höhe h gilt cos(alpha/2)=h/r oder h=r*cos(alpha/2).
Für die Sehne s gilt sin(alpha/2)=(s/2r) oder s=2r*sin(alpha/2).
Damit ist A''=(pi*alpha*r²)/360°-(sh)/2=pi*alpha*r²/360°-r²*sin(alpha/2)*cos(alpha/2).
A''=pi*alpha*r²/360°-(r²/2)*sin(alpha)=[pi*alpha/180°-sin(alpha)]*(r²/2). |
Zur Kontrolle: Wählt man einen Halbkreis und setzt alpha=180°,
so ergibt sich A''=(pi/2)*r².
 Weitere Kreisteile findet man an anderer Stelle
meiner Homepage.
Weitere Kreisteile findet man an anderer Stelle
meiner Homepage.
Bogenmaßtop
Definition des Winkels
...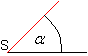 ... ... |
Ein Winkel entsteht, wenn man eine Halbgerade in horizontaler
Lage festhält und eine andere Halbgerade, die vom gleichen Endpunkt
ausgeht, in positiver Richtung dreht. |
Gradmaß
... ... ... |
Will man die Größe eines Winkels messen, so
muss man die Drehung messen.
Dazu führt man das Gradmaß ein, bei dem einer
Volldrehung die Winkelgröße 360° entspricht. Von da aus
kommt man zu kleineren Winkeln. |
Bogenmaß
Es gibt eine zweite, einfachere Definition des Winkelmaßes.
...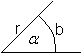 ... ... |
Ein Winkel ist eine Figur aus zwei Halbgeraden, die von
einem Punkt ausgehen.
Zeichnet man in die Figur noch einen Kreisbogen, so sind
bei festem Winkel die Bogenlänge b und der Radius r proportional. |
Der Quotient b/r ist ein Maß für die Größe
des Winkels und heißt Bogenmaß.
Die Einheit ist 1m/m für b=1m und r=1m, also ist
b/r dimensionslos.
Wählt man einen Vollkreis
mit dem Radius 1, so ist der Umfang das Bogenmaß eines Winkels mit
dem Winkelmaß 360°.
Es gilt also 2*pi=360°. Damit deutlich wird, dass
auch 2*pi ein Winkelmaß ist, fügt man Radiant oder rad hinzu:
2*pi rad=360°. Daraus folgt 1 rad=180°/pi oder
angenähert 1 rad=57,3°.
Obwohl das Bogenmaß
eine natürliche Einheit ist und auch im internationalen Einheitensystem
(SI-System) bevorzugt wird, ist in der Schulmathematik das Gradmaß
üblich, solange die Kreislehre noch nicht behandelt wurde.
... ... ... |
Der Taschenrechner gibt noch einen Hinweis auf eine dritte
Winkeleinheit, auf 1 Neugrad oder jetzt offiziell 1 gon. Da wird der rechte
Winkel nicht mit 90°, sondern mit 100 gon oder 100g gemessen. |
Dieses Vorhaben, das Dezimalsystem auch für Winkel einzuführen,
ist nach meiner Kenntnis nur in der Geodäsie verwirklicht.
Zur Definition
der Kreislinie top
Umfangswinkelsatz
Oben wird der Kreis über die Entfernung von einem
festen Punkt M definiert. Das ist eine anschauliche Definition und wird
bei einer ersten Einführung des Kreises verwendet. Sie setzt voraus,
dass ein Abstandsbegriff definiert ist. Viele Sätze zum Kreis, zum
Beispiel die Winkelsätze, erfordern das gar nicht. Da steht der Umfangswinkelsatz
(Peripheriewinkelsatz) an zentraler Stelle.
...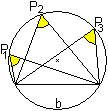 ... ... |
Er heißt:
Alle Umfangswinkel (Peripheriewinkel) über einem
Kreisbogen b sind gleich groß.
Dieser Satz ist charakteristisch für den Kreis.
D.h., er ist umkehrbar. |
Somit kann die Definition der Kreislinie auch lauten:
Eine Kreislinie ist die Menge aller Scheitelpunkte der
Winkel, die über einem Kreisbogen liegen und gleich sind.
Quelle: (1) Seite 126ff.
"Eine kennzeichnende Eigenschaft des Kreises"
Thalessatz
...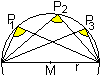 ... ... |
Der Satz des Thales besagt, dass jeder Winkel im Halbkreis
ein rechter Winkel ist. Auch dieser Satz ist umkehrbar und kann der Definition
der Kreislinie dienen. |
Sie lautet:
Eine Kreislinie ist die Menge aller Scheitelpunkte der
rechten Winkel, die über einer Strecke liegen.
Kreis
des Apollonios
...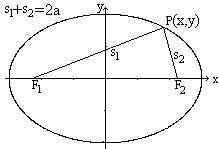 ... ... |
Der Kreis ist der Spezialfall einer Ellipse.
Eine Ellipse kann definiert werden als die Ortslinie
aller Punkte, deren Summe der Entfernungen von zwei festen Punkten konstant
ist.
Es stellt sich die Frage, ob und dann wie man die Bedingung
so abändern kann, dass sich an Stelle der Ellipse ein Kreis ergibt. |
Das führt zum sogenannten
Apollonios-Kreis (Apollonios von Perge).
...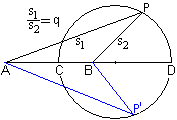 ... ... |
Man gibt zwei Punkte A und B und eine Zahl q vor. Dann
sucht man die Punkte P, für die AP:BP=q gilt. Zwei Punkte P und P'
werden stellvertretend eingezeichnet.
Es gilt die Aussage: Alle Punkte, deren Quotient der Länge
der Entfernungen von zwei festen Punkten A und B konstant ist, liegen auf
einer Kreislinie.
|
Zum Beweis
...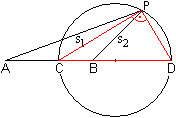 ... ... |
Zum Beweis kennzeichnet man die Schnittpunkte der Geraden
AB und des Kreises mit C und D. Verbindet man diese Punkte mit einem Kreispunkt,
so kann man zeigen, dass CPD ein rechter Winkel ist. Nach der Umkehrung
des Thalessatzes ist P ein Kreispunkt. |
Es ist erwähnenswert, dass der Punkt C die Strecke AB
innen im gleichen Verhältnis teilt wie der Punkt D außen. Es
handelt sich um eine harmonische Teilung.
Kreis
im kartesischen Koordinatensystem top
Allgemeine Gleichung
...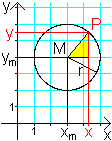 ... ... |
Gegeben sei ein Kreis mit dem Radius r und dem Mittelpunkt
M(xm|ym).
Es sei P ein beliebiger Kreispunkt P(x|y).
Dann gilt nach dem Satz des Pythagoras die Gleichung
(x-xm)²+(y-ym)²=r².
Umgekehrt gilt: Erfüllen die Koordinaten eines Punktes
P die Gleichung (x-xm)²+(y-ym)²=r²
gilt, so ist P ein Kreispunkt.
In der nebenstehenden Zeichnung gilt (x-3)²+(y-4)²=4 |
Mittelpunktgleichung
Liegt der Mittelpunkt des Kreises im Nullpunkt des Koordinatensystems,
so ist xm=0 und ym=0.
Die Kreisgleichung lautet dann x²+y²=r².
Gleichung
zweiten Grades
Multipliziert man die Quadrate in der allgemeinen Gleichung
(x-xm)²+(y-ym)²=r² aus, so erhält
man x²+y²-2xmx-2ymy+xm²+ym²-r²=0.
Diese Gleichung hat die Form x²+y²+Ax+By+C=0.
Es stellt sich die Frage, welche Bedingungen A, B und C erfüllen müssen,
damit diese Gleichung einen Kreis darstellt. Zum Beispiel darf A=B=C=0
nicht gelten. Dann ist nämlich x²+y²=0 und nur der Nullpunkt
erfüllt die Gleichung.
Zunächst einmal formt man die Gleichung zu (x-A/2)²+(y-B/2)²=(A/2)²+(B/2)²-4C
um. Nach der allgemeinen Gleichung oben muss der rechte Term (A/2)²+(B/2)²-4C
dem Quadrat r² entsprechen. Also muss (A/2)²+(B/2)²-4C>0
oder A²+B²>4C sein.
Ergebnis: Die Gleichung zweiten Grades der Form x²+y²+Ax+By+C=0
stellt genau dann einen Kreis dar, wenn A²+B²>4C ist.
Quelle: (3) Seite 351ff.
Kreis
halbieren
top
Halbkreis
.. .... ....
|
Einen Durchmesser einzuzeichnen ist die einfachste Art,
einen Kreis zu halbieren.
An anderer Stelle meiner Homepage findet man eine Webseite
nur über den Halbkreis. |
Die
grasende Ziege
Diese Halbierung ist Gegenstand des bekannten Problems
"The grazing goat".
...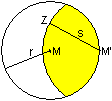 ... ... |
Gegeben sei eine kreisförmige Grasfläche. Im
Randpunkt M' ist ein Pflock eingeschlagen, an dem ein Seil befestigt ist.
An dessen Ende steht eine Ziege Z. Wie groß muss die Länge s
des Seils sein, damit die Ziege die Hälfte der Kreisfläche mit
dem Radius r erreichen kann? |
Diese einfach und harmlos erscheinende
Aufgabe hat es in sich.
...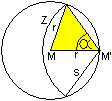 ... ... |
Es ist ungeschickt, die Sehne s
als Suchvariable einzuführen. Besser ist der eingezeichnete Winkel
alpha.
Dann erhält man die Gleichung
pi/2
+ 2alpha * cos(2alpha) - sin(2alpha) = 0 mit
der Näherungslösung alpha = 0.9528 rad=54.6°.
Das führt zur einer Länge
des Seils von s=1,1587r. |
Näheres bei Hans Henschel (URL unten).
Yin
und Yang
.. .... .... |
Von dieser Figur weiß wohl jeder, dass sie etwas
mit der chinesischen Kultur und mit männlich/weiblich zu tun hat.
Wer etwas Genaueres wissen will, findet bei Wikipedia
einige Informationen (URL unten).
Die Figur passt hier, da der Kreis auch so in zwei Hälften
geteilt wird. |
Zirkel top
Das Zeichengerät zum Zeichnen
eines Kreises ist der Zirkel.
Vorstellung dreier Zirkel
1
... ... ... |
Wer kennt ihn noch?
Ich hatte schon vergessen, dass früher diese Art
von Zirkel üblich war.
In England habe ich ihn noch gefunden. |
2
Dieses ist ein einfacher Schulzirkel,
den ein Lehrer bei den Schülern gerade noch durchgehen lassen kann.
1 Die Spitze ist nur eingeklemmt. Besser wäre es, wenn
sie herausnehmbar und so auch in der Länge verstellbar wäre.
2 Die Bleistiftmine wird durch einen Schraubmechanismus
festgehalten und kann in der Länge passend verändert werden.
3 Unentbehrlich ist eine Schraube
an dieser Stelle. Man muss sie anziehen können, wenn der Zirkel ausleiert,
wenn also die Schenkel sich zu leicht bewegen lassen.
4 An diesem Griff fasst man den
Zirkel an. Etwas bessere Zirkel haben einen Führungsmechanismus für
die Schenkel, so dass das Stäbchen immer in Richtung der Winkelhalbierenden
der Schenkel zeigt.
3
... ... ... |
Das ist der Zirkel, der heute oft gekauft wird und den
sich Schülerinnen und Schüler gerne gönnen.
Ein Nachteil ist die mühselige Veränderung
des Radius.
Einen zweiten Nachteil erkennt man an diesem Exemplar.
Die auf dem Foto vertikal liegende Führungsschraube ist krumm. Das
passiert leicht. Ein neuer Radius ist jetzt schwer einstellbar. |
Zeichenübungen
... ... ... |
Es ist gar nicht so leicht, mit dem Zirkel sachgerecht
umzugehen. Man muss lernen, nur die Spitze zu belasten.
Eine beliebte Hausaufgabe ist für Anfänger,
eine Rosette und eine Zielscheibe als Pflicht-, ein Männchen und einen
Hasen als Kür-Figuren zu zeichnen :-). |
Mittelpunkt
suchen
... ... ... |
Anfänger vergessen oft, vor dem Zeichnen eines Kreises
den Mittelpunkt durch ein Kreuz festzulegen.
Dann stellt sich das Problem, den Mittelpunkt des schon
gezeichneten Kreises zu finden. |
Ist der Radius noch eingestellt, so genügen zwei Kreise
mit einem Mittelpunkt auf der Kreislinie.
Sonst muss man zu je zwei Punktepaaren auf der Kreislinie
mindestens zwei Mittelsenkrechte zeichnen.
Da ist das Geodreieck mit den symmetrischen Skalen hilfreich.
Zur Quadratur
des Kreises
top
Es geht dabei um das sprichwörtlich gewordene Problem,
einen Kreis in ein flächengleiches Quadrat zu verwandeln.
Dabei ist Bedingung, dass die Quadratseite nur mit Zirkel
und Lineal aus dem Radius konstruiert werden muss.
Ohne diesen Zusatz ist die Lösung einfach. Der Ansatz
pi*r²=x² führt zu x=sqrt(pi)*r oder angenähert x=1,77r.
Seit Ferdinand von Lindemann
1882 der Beweis gelang, dass pi eine transzendente Zahl ist, weiß
man, dass die Quadratur des Kreises nicht möglich ist.
Trotzdem liest man immer wieder mal in der Zeitung, dass
jemand, der offenbar nicht mit der Theorie vertraut ist, angeblich eine
Lösung gefunden und es den studierten Mathematikern gezeigt hat.
Ich war der Meinung, dass Ferdinand von
Lindemann auf seinem Grabstein voller Stolz nur die Zahl pi als Dezimalzahl
mit etlichen Dezimalen einmeißeln ließ. Das ist eine schöne
Geschichte, die zu meinem Repertoire als Lehrer gehörte. Ich übernahm
sie von einem meiner Lehrer. Sie ist falsch.
... ... ... |
Im Internet fand ich ein Foto seines Grabsteins. Er enthält
die üblichen Daten seiner Person und die seiner Frau, einer Schriftstellerin.
Immerhin steht oben auf dem Grabstein pi und eine Kreis/Quadrat-Kombination.
Das ist vielleicht eine noch schönere Geschichte. |
Das vollständige Foto findet man bei Wolfgang Volk (URL
unten)
Ergänzung
Die Schülerin Rebecca fand im Rahmen ihrer Jahresarbeit
heraus, dass der mit pi auf dem Grabstein offenbar nicht Lindemann, sondern
Ludolph van Ceulen war, wie man auf der Wikipedia-Webseite (URL unten)
nachlesen kann. Da habe ich wohl als Schüler nicht aufgepasst, peinlich.
Eulenlochtop
Und nun zu einem Kapitel mit Lokalkolorit.
Zu sehen sind die Giebel dreier
Häuser in der Heldmannstraße in Bad Salzuflen, Ortsteil Schötmar.
Die kreisförmigen Fenster waren früher meist ein
einfaches Loch wie bei Nr.9 noch zu sehen ist. Die Öffnungen hießen
Eulenloch oder auf lippisch Platt Iulenlock. Sie waren für Schleiereulen
bestimmt. Früher lebten sie auf Dachböden als willkommene Gäste
und hielten den Boden (weitgehend) mäusefrei.
Haus Nr. 8 ist auch ein altes Haus, doch das Eulenloch
ist heute geschlossen.
Nr.4 ist ein Neubau von 2005. Der Kreis ist so etwas
wie das Zitat eines Eulenlochs. Da war ein sensibler Architekt tätig.
Kreis im Internet
top
Deutsch
Hans Henschel
Rätsel
/Die grasende Ziege, Lösung
Wikipedia
Kreis
(Geometrie), Kreissegment,
Kreissektor,
Kreis
des Apollonios, Pi
(Kreiszahl),
Peripheriewinkel,
Satz
des Thales,
Zirkel
(Gerät), Winkel
(Geometrie), Grad
(Winkel), Bogenmaß,
Gon,
Eulenloch,
Yin
und Yang,
Ludolph
van Ceulen
Wolfgang Volk
Grab
von Ferdinand von Lindemann in München (Deutschland)
Englisch
Eric W. Weisstein (MathWorld)
Circle
Wikipedia
Circle,
List
of circle topics
youtube
Two-circle
roller, World
Freehand Circle Drawing Champion
Auf meiner Homepage gibt
es an anderen Stellen etliche Informationen zum Kreis.
Kreisausschnitt, Kreisteile,
Halbkreis,
Sehnenviereck,
Tangentenviereck,
Kreise
im Kreis, Arbelos,
Gleichdick,
Achtkurve,
Kugel,
Zweikreisfiguren,
Salinon
Referenzen top
(1) Rademacher-Toeplitz: Von Zahlen und Figuren, Springer,
Berlin, Heidelberg, New York1968 (Nachdruck von 1930)
(2) C.Stanley Ogilvy: Unterhaltsame Geometrie, Braunschweig
1975 [ISBN 3 528 08314 x]
(3) Heinz Nickel (federführend): Algebra und Geometrie
für Ingenieur- und Fachschulen, Frankfurt/M. und Zürich, 1966.
(4) Jean-Paul Delahaye: Pi - Die Story, Basel, Boston,
Berlin 1999 [ISBN 3-7643-6056-9]
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |
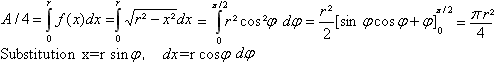
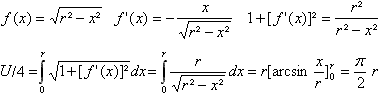
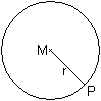 ...
...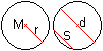
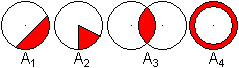


 ...
... ...
...
 ...
...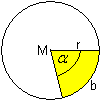
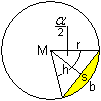 ...
... ...
...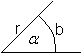 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ....
.... ...
... ...
... ....
.... ...
...

 ...
... ...
... ...
... ...
...

