|
Was ist ein 30-60-90-Dreieck?
...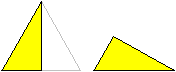 ... ... |
Halbiert man ein gleichseitiges Dreieck durch eine Höhe,
so entsteht ein Dreieck mit den Innenwinkeln 30°, 60° und 90°.
Deshalb nennt man es auch 30-60-90-Dreieck. |
Das Besondere an diesem Dreieck ist, dass die Innenwinkel
im Verhältnis 1:2:3 stehen.
Wenn auf dieser Seite von einem Dreieck
die Rede ist, dann ist es meist das 30-60-90-Dreieck.
Größen
des Dreiecks
top
...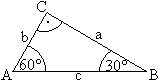 ... ... |
Ist die Hypotenuse des Ausgangsdreiecks gleich c,
so sind die Katheten b=(1/2)c und a=(1/2)sqr(3)c. Für
das Seitenverhältnis gilt a:b:c = sqrt(3):1:2.
Der Flächeninhalt ist A=(1/2)ab=(1/8)sqr(3)c². |
Der Umfang ist U= a+b+c = (1/2)[(3+sqr(3)]c.
...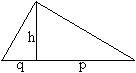 ... ... |
Da das 30-60-90-Dreieck rechtwinklig ist, gibt es nur
eine Höhe h, die anderen Höhen fallen mit den Katheten zusammen.
Die Höhe teilt die Hypotenuse c in die Hypotenusenabschnitte p und
q. |
Es gilt h=(1/4)sqr(3)c [folgt aus den Flächenformeln
(1/2)ab=(1/2)ch]
und p=(3/4)c, q=(1/4)c [folgt aus
dem Kathetensatz pc=b² bzw. qc=a²].
... ... ...
|
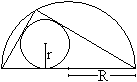
Wie jedes Dreieck hat das 30-60-90-Dreieck einen Umkreis
und einen Inkreis.
Der halbe Umkreis ist der Kreis des Thales mit dem Radius
R=c/2.
Der Radius des Inkreises ist r=(1/4)[3 - sqr(3)]c. |
Rechnung zum Radius r
...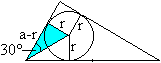 ... ... |
Man betrachte das blaue Dreieck. Es gilt tan(30°)
= r/(a-r). Setzt man tan(30°)=1/sqr(3) und a=c/2, so ergibt sich nach
einigen Umformungen r = (1/4)[3 - sqr(3)]c. |
Quadrate im Dreieck
top
... ... ...
|
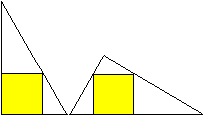
Man kann ein Quadrat auf zweierlei Weise in ein 30-60-90-Dreieck
legen.
Sind die Quadrate gleich groß? |
Lösung
...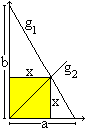 ... ... |
Zur Lösung legt man das Dreieck in ein Koordinatensystem
und betrachtet die Geraden g1 und g2.
Die Gerade g1 :f(x)=-(b/a)*x+b enthält
die Hypotenuse,
die Gerade g2 : g(x)=x ist die 1.Winkelhalbierende
und enthält zwei Ecken des Quadrates.
Für den Schnittpunkt der beiden Geraden gilt f(x)=g(x)
oder x = -b/a*x+b oder x=ab/(a+b). |
Herleitung
x = -b/a*x+b
|*a
ax=-bx+ab
|+bx
ax+bx=ab | x ausklammern
(a+b)x=ab |:(a+b)
x=ab/(a+b)
... ... ...
|
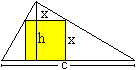
Nach dem 2.Strahlensatz (leicht abgewandelt) gilt h:c
= (h-x):x. Daraus folgt x=hc/(h+c). |
Die Ergebnisse sind bemerkenswert: Die halben Quadratseiten
sind in beiden Fällen ein harmonisches Mittel, einmal das von Höhe
und Hypotenuse, zum anderen das der beiden Katheten.
Die Aussagen gelten übrigens für beliebige
rechtwinklige Dreiecke.
Setzt man die Größen des
30-60-90-Dreiecks ein, so ergibt sich
im ersten Falle x=(1/4)[3-sqr(3)]c (ungefähr 0,32c),
im zweiten Fall x=(1/13)[4sqr(3)-3]c (ungefähr 0,30c).
Figuren
aus 30-60-90-Dreiecken
top
Quadrate, gleichseitige Dreiecke
oder gleichschenklig-rechtwinklige Dreiecke kann man so aneinanderlegen,
dass neue Figuren entstehen. Sie heißen dann Polyominos (Pentominos
oder
Hexominos),
Polyiamonds
oder Polybolos.
Natürlich kann man auch aus
30-60-90-Dreiecken
neue Figuren bilden.
... ... ...
|
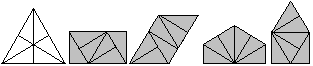
Man kann zwei Dreiecke schon auf sechs verschiedene Arten
zusammensetzen. Als Puzzlestücke sind sie nicht gut geeignet, weil
alle Strecken voneinander verschieden sind. |
Die Frage ist: Wie viele Figuren kann man aus drei (vier,
...) Dreiecken legen?
Allerdings: Diese Figuren kommen beim Eternity-Spiel
vor und heißen Polydrafter (Siehe Linkliste).
Figuren aus
sechs Dreiecken
... ... ...
|
Zeichnet man in ein gleichseitiges Dreieck alle Höhen
ein, so entstehen sechs 30-60-90-Dreiecke. Man kann sie als Tangram-Steine
benutzen. (1) |
Eine Figur
aus acht Dreiecken
...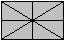 ... ... |
Zeichnet man in ein Rechteck die Diagonalen und die Mittellinien,
so entstehen acht rechtwinklige Dreiecke.
Die Figur entspricht der englischen Nationalflagge. Im
Allgemeinen sind die Dreiecke keine 30-60-90-Dreiecke. Nur wenn die Fahne
das Format sqr(3):1 hat, gilt dieses. |
Zum Vergleich: Das Din-Format hat das Seitenverhältnis
sqr(2):1.
Spirale
...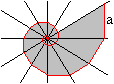 ... ... |
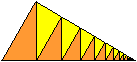
Sechs Geraden treffen sich in einem Punkt und bilden
12 Winkel der Größe 30°.
Gibt man die vertikale Strecke der Länge a vor und
führt sie in den Winkelräumen fort, indem man eine Senkrechte
zur nächsten Halbgeraden zeichnet, so entsteht eine Folge von immer
kleiner werdenden 30-60-90-Dreiecken. Die kürzeren Katheten bilden
eine Spirale (rot).
Welchem Grenzwert nähert sich die Länge der
Spirale, wenn a gegeben ist? |
Lösung
... ... ...
|
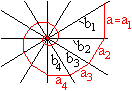
Gegeben sei a.
Die Folge der Hypotenusen b1, b2,
b3, b4,... bilden eine geometrische Folge. |
b1=2a
b2 = [(1/2)sqr(3)](2a)
b3 = [(1/2)sqr(3)]b2 = [(1/2)sqr(3)]²(2a)
b4 = [(1/2)sqr(3)]b3 = [(1/2)sqr(3)]³(2a)
...
Für die kürzeren
Katheten, die die Spirale bilden, gilt:
a1 =a
a2 = (1/2)b2 = [(1/2)sqr(3)]a
a3 = (1/2)b3 = [(1/2)sqr(3)]²a
a4 = (1/2)b4 = [(1/2)sqr(3)]³a
...
Das ist eine geometrische Folge. Die zugehörige
Reihe hat den Grenzwert 1/(1-q) = [4+2sqr(3)]a
(ungefähr 7.46a).
Noch zwei Figuren
... ... ...
Dreiecke in einem 30-60-90-Dreieck
|

Ein Stern aus neun Dreiecken
|
Zwei Kegel top
... ... ... ... ...
|
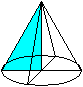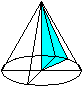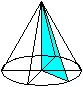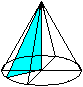
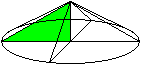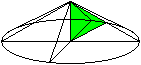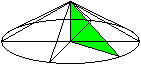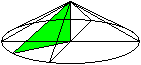
Es entstehen zwei Kegel, wenn das Dreieck je um eine
der beiden Katheten rotiert.
V(a) sei das Volumen bei Rotation um a, V(b) um b.
Die Volumina der beiden Kegel stehen im Verhältnis
V(b):V(a) = sqr(3):1. |
Das Dreieck kann sich auch
um die Hypotenuse drehen. Dann entsteht ein Doppelkegel mit V(q):V(p)=3:1.
Eternity Puzzle
top
... ... ... |
... ... ... |
Bekannt sind Puzzles, bei denen man aus einzelnen Stücken
ein rechteckiges Bild zusammensetzen soll.
In diesem Falle gibt es 24 Stücke. |
Im Juni 1999 brachte die britische Firma Racing Champions
Ltd das sogenannte Eternity Puzzle auf den Markt. Erfinder war Christopher
Monckton. Nach (2) wurde das Puzzle mehr als 250 000 mal verkauft.
... ... ...
|
... ... ...
|
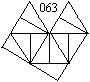
Das Puzzle besteht aus 209 Teilen. Jedes Teil besteht
aus zwölf 30-60-90-Dreiecken.
Mit diesen Teilen soll ein fast regelmäßiges
Zwölfeck ausgelegt werden.
Ist a die Länge der Seite und h die Höhe des
gleichseitigen Dreiecks, so hat das Zwölfeck abwechselnd die Seiten
7a und 8h. |
Im Mai 2000 lösten zwei Mathematiker aus Cambridge das
Puzzle zuerst - mit Computerhilfe.
Mehr findet man über meine Linkliste.
30-60-90-Dreieck
im Internet top
Deutsch
Wikipedia
Eternity-Puzzle
Englisch
Eric W. Weisstein (MathWorld)
30-60-90
Triangle, Eternity,
Polydrafter
Ed Pegg Jr. (Math Puzzles)
THE
ETERNITY PUZZLE
John Page
30°-
60°- 90° Triangle
Lawrence Spector (TheMathPage)
THE
30°-60°-90° TRIANGLE
Wikipedia
30-60-90
triangle, Eternity
puzzle
Referenzen top
(1) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (ISBN
3-7701-2097-3)
(2) Ingo Althöfer: Eine Million britische Pfund
für zwei Mathematiker, Magazin Omega, Spektrum Spezial 4/2003
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...


 ...
... ...
... ...
... ...
... ...
...