|
Was ist ein Triomino-Puzzle?
... ... ... |
Das sind die Triominos.
Unter Triomino-Puzzles fasse ich die Aufgaben zusammen,
aus den Spielsteinen nach einer Vorschrift Figuren zu legen.
|
...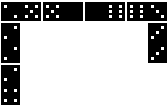 ... ... |
Domino ist ein bekanntes Gesellschaftsspiel,
bei dem mindestens zwei Spieler nacheinander Dominosteine passend ablegen.
Gewonnen hat der, der zuerst seine Steine abgelegt hat.
Links eine Darstellung aus der ersten Phase des Spiels. |
...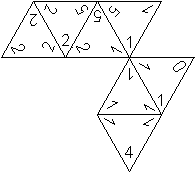 ... ... |
Triomino ist eine Erweiterung.
Statt der Doppelquadrate sind die Spielsteine oder Triominos
gleichseitige Dreiecke, die in den Ecken die Ziffern 0, 1, 2, 3,
4 oder 5 tragen. Zwei Spieler oder mehr legen sie abwechselnd so aneinander,
dass die Ziffern an einer Ecke übereinstimmen. Gewonnen hat (nach
einer Spielregel unter mehreren) derjenige, der zuerst die Steine abgelegt
hat.
Links eine Darstellung aus der ersten Phase des Spiels. |
Auf das Spiel Triomino soll hier nicht eingegangen werden,
sondern auf Puzzles mit Triominos.
Offenbar gibt es viele Hersteller
des Triomino-Spiels, die ihm dann gerne einen eigenen Namen geben. Auf
der Webseite BoardGameGeek (URL unten) werden 23 Namen genannt. Dabei ist
die Liste nicht vollständig. Ich nenne noch Tridom. - Am Ende dieser
Seite gehe ich noch auf die Varianten Troiker, Trominos und
MacMahons
Farbdreiecke ein.
Aufbau der Triominos
top
Das mir vor Jahren geschenkte
Triominos Pocket (Spiel) (©
Goliath BV,NL 8051 KR Hattem)
ist wohl eine Standard-Version, was die Beschriftung der
Steine und die Anzahl 56 angeht.
Es stellt sich die Frage, wie die Ziffern 0, 1 , 2, 3,
4 und 5 auf den Triominos verteilt sind und wie die Anzahl 56 einzuordnen
ist.
Ordnen
der Triominos.
Die Triominos sollen dreistellige Zahlen als Namen bekommen.
...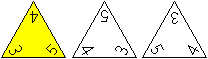 ... ... |
Der Spielstein mit den Ziffern 3, 4 und 5 könnte
zum Beispiel die Namen 345, 453 oder 534 tragen. Dabei beachtet man den
Uhrzeigersinn. |
Er wird eindeutig, wenn man die kleinste dreistellige
Zahl wählt. Das ist hier 345.
Es folgen alle 56 Triominos
in dieser Schreibweise. Sie sind der Größe nach geordnet.
000 001 002 003 004 005 011 012 013 014 015 022 023 024
025 033 034 035 044 045 055
111 112 113 114 115 122 123 124 125 133 134 135 144 145
155
222 223 224 225 233 234 235 244 245 255
333 334 335 344 345 355
444 445 455
555
Man stellt fest, dass die
einstelligen Zahlen, deren Ziffern die dreistelligen Zahlen bilden, gleich
bleiben oder ansteigen. Und da gibt es alle Möglichkeiten.
...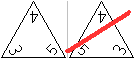 ... ... |
Das bedeutet, dass unter den Triominos Steine wie 354
nicht vorkommen.
Man verzichtet damit auf Paare achsensymmetrischer Steine. |
Die
Formel hinter der Anzahl 56
Dazu werden die 56 Triominos neu geordnet, und zwar nach
der Anzahl der Ziffern.
In jeder Zeile taucht eine weitere Ziffer auf.
000
001 011 111
002 012 022 112 122 222
003 013 023 033 113 123 133 223233 333
004 014 024 034 044 114 124 134 144 224 234 244334 344
444
005 015 025 035 045 055 115 125 135 145 155 225 235 245
255 335 345 355 445 455 555
Die Anzahl ergibt sich, wenn
man die Tripel zeilenweise abzählt. Es gilt 1+3+6+10+15+21=56.
Die Summanden bilden die Dreieckszahlen,
die Folge der Partialsummen die Tetraederzahlen.
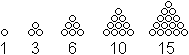
Dreieckszahlen
|
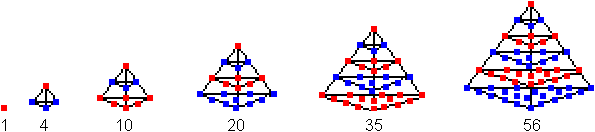
Tetraederzahlen
|
Das n-te Glied der Folge
der Tetraederzahlen aber ist T(n)=(1/6)n(n+1)(n+2).
Setzt man n=6, ergibt sich 56.
Puzzles ohne
Domino-Regel top
Figuren aus Dreiecken
Man kann die Triominos einfach aneinanderlegen, ohne
darauf zu achten, ob Ecken mit entsprechende Ziffern aneinanderstoßen,
so dass mehr oder weniger ansehnliche Figuren entstehen.
Ich stellte mir die Aufgabe, nacheinander die Triominos
nach Ziffern getrennt und dann alle Triominos zu einem Dreieck anzuordnen.
Das gelang nur mit dem Triomino-Satz mit zwei Ziffern,
immerhin kann man sich Dreiecken annähern.
Puzzles mit
Domino-Regel top
Die folgenden Möglichkeiten, mit den Triominos zu
spielen, sollen Anregungen sein.
Polyiamonds
Polyiamonds sind Figuren, die
man aus kongruenten, gleichseitigen Dreiecken bilden kann. Bekannt sind
die Hexiamonds, die Iamonds aus 6 Dreiecken. Ein Problem ist, eine
Figur aus 12*6=60 Dreiecken zu entwerfen und sie dann mit den "Hexiamonds"
auszulegen.
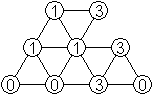
Man kann die einzelnen Hexiamonds
aus sechs Triominos unter Berücksichtigung der Domino-Regel legen.
Da das leicht ist, kann man sich auf möglichst wenige Ziffern beschränken.
...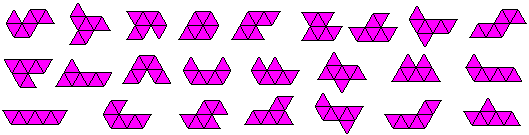 ... ... |
Es ist sicher auch möglich, die 24 Heptiamonds mit
Triominos auszulegen.
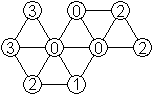
|
Dreiecke aus
Triominos
Sechsecke
aus Triominos
Die folgende Figur aus acht
Sechsecken schickte mir Frank, der auch die Anregung für das Erstellen
dieser Webseite gab.
Götz schickte mir u.a. eine abgeänderte Figur mit
einem Sechseck mehr.

Im November 2024 schickten
mir Norri + Balduin auch eine Lösung mit acht Sechsecken. Fast wären
es neun geworden. Sie schreiben: "Der Stein", der sich nicht einfügen
lässt, "wird als Strafe von dem „Triominos-Monster“ gefressen :-D".

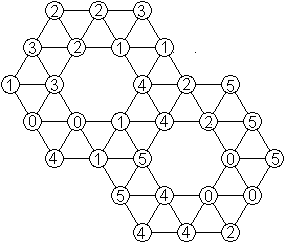
Ein
Sechseck aus 32 Steinen
...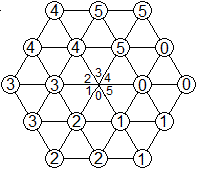 ... ... |
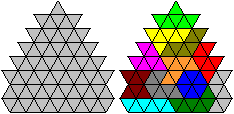
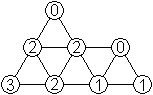
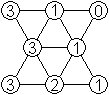
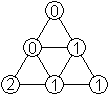
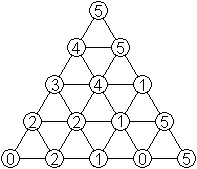
Im Internet fand ich mehrfach dieses schöne Sechseck.
In der Mitte konnte die Anlegeregel nicht erfüllt
werden.
Aber dafür stehen dort die Zahlen von 0 bis 5 und
außen alle Zahlen dreimal in der natürlichen Reihenfolge................................................ |
Ringe
"Viele Sechsecke"
Es stellt sich die Frage, wie viele verschiedene Sechsecke
man mit den Triominos legen kann.
...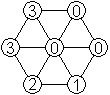 ... ... |
Da keine Ziffer bei der Verteilung auf die Dreiecken
bevorzugt oder benachteiligt wird, müsste man neue Figuren erhalten,
indem man die Ziffern austauscht. |
...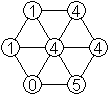 ... ... |
Das heißt zum Beispiel, dass man die Ziffern 0,
1, 2, 3 durch 4, 5, 0, 1 ersetzt.
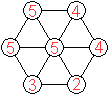
Das führt zum nebenstehenden Sechseck, das in der
Tat auch existiert. |
Nach der Theorie gibt es
6! Möglichkeiten, die Ziffern 0, 1, 2, 3, 4, 5 umzuordnen (zu permutieren).
Damit ist die Anzahl der möglichen Sechsecke 1*2*3*4*5*6=720.
... ... ... |
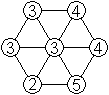
Doch Vorsicht! Ersetzt man zum Beispiel die Ziffern 0,
1, 2, 3 durch die Ziffern 3, 2, 5, 4, so gibt es eine Schwierigkeit. Das
entworfene Sechseck links gibt es nicht. Dafür gibt es das achsensymmetrische
Sechseck rechts. Die Achse liegt vertikal. |
... ... ... |
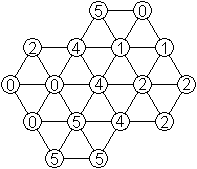
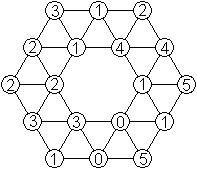
Es gibt noch viele weitere Sechsecke.
... ... ... |
 ... ...
|
 ... ...
|
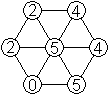
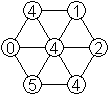
Die beiden neuen Sechsecke rechts haben andere Strukturen.
Im mittleren Sechseck fehlt das Dreieck aus gleichen
Ziffern,
im rechten auch die beiden Ziffernpaare auf dem Rand. |
Es ist wohl sinnvoll, nur diese drei Sechsecke als verschieden
anzusehen.
Sechsecke
und ihre Augenzahl
Man kann die Sechsecke unter einem anderen Gesichtspunkt
betrachten.
Man addiert die Augenzahl und ordnet die Summe einem
Sechseck zu.
Das sind die bisher angegebenen Sechsecke mit ihren Summen.
...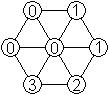 ... ...
7
|
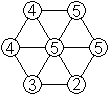 ... ...
28
|
Dann kann man Sechsecke gleicher Augenzahl oder - wie
hier - das Sechseck mit möglichst kleiner bzw. möglichst
großer Augenzahl suchen. |
Sechsecke
mit gleichem Umfang
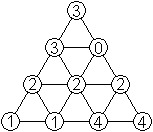
|
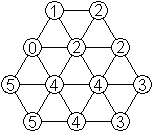
|
Die beiden Figuren haben eine gemeinsame Eigenschaft:
Sie haben den gleichen Umfang, nämlich 9 Längeneinheiten. |
Man kann sich die Aufgabe
stellen, neue Figuren mit dem Umfang 9 zu entwerfen und zu lösen.
Ablegen
aller Triominos
...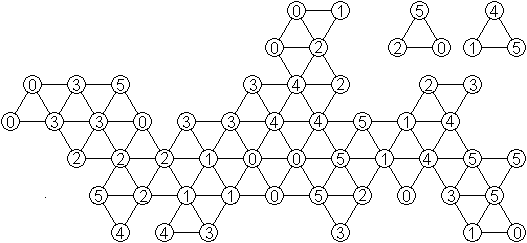 ... ... |
Es gelang mir nicht, ein zusammen hängendes Gebiet
ohne Löcher aus allen Triominos zu legen.
Zwei Dreiecke blieben übrig. |
Frank fand die folgende perfekte
Lösung.
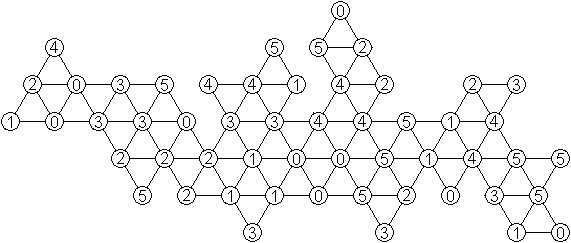
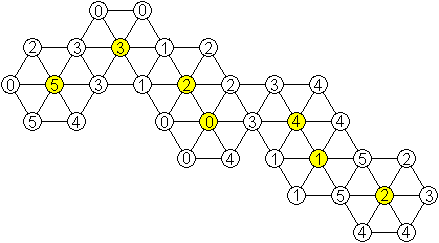
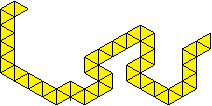
Ketten aus Triominos
Harald Hiessl beschäftigte sich mit dem Problem,
die Triominos linear anzuordnen. Er fand bisher sechs Lösungen.
Das ist eine Lösung.

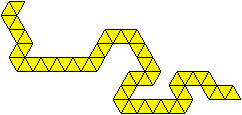
Struktur von drei weiteren
Lösungen
Er stellt folgende Fragen.
> Wie viele Anordnungen gibt es?
> Gibt es eine Konstruktionsregel?
> Gibt es eine geschlossenen Anordnung?
Das ist mit 42 Triominos
vielleicht die längste Kette längs einer Geraden. Oder?
...
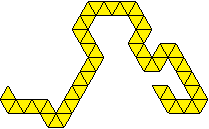
Ablegen
aller Triominos
Walter Keil spielt Triomino so. Ein Stein liegt offen
auf dem Tisch und weitere werden nach den üblichen Regeln an eine
passende Stelle angelegt. Ziel ist es allein, am Ende alle Steine abgelegt
zu haben, es soll also keiner übrig bleiben. Er schreibt, dass es
selten passiert.
Dieses ist eine seiner bisher gefundenen sieben Lösungen.

Er fragt, ob es wohl ein Programm dafür geben könnte
dies auszurechnen?
Jo Flacke sandte mir eine Figur mit zwei Löchern,
in der auch alle Triominos verwendet werden.

Troiker top
Das oben vorgestellte Triominos besteht aus 56 Dreiecken,
die die sechs Ziffern 0, 1, 2, 3, 4 und 5 tragen.
000 001 002 003 004 005 011 012 013 014 015 022 023 024
025 033 034 035 044 045 055
111 112 113 114 115 122 123 124 125 133 134 135 144 145
155
222 223 224 225 233 234 235 244 245 255
333 334 335 344 345 355
444 445 455
555
Beschränkt man sich
auf die vier Ziffern 0, 1, 2 und 3, so kommt man auf 20 Dreiecke.
000 001 002 003 011 012 013 022 023 033
111 112 113 122 123 133
222 223 233
333
Das sind 20 Steine des Spiels Troiker, wobei noch vier
Steine fehlen.
Es gibt vier Steine mit drei verschiedenen Ziffern, nämlich
012 013 023 123, zu denen es noch vier achsensymmetrische gibt: 021
031 032 132. Die 24 Steine bilden das Spiel Troiker.
... ... ... |
Statt der Ziffern stehen auf den Dreiecken die Augen,
die man vom Domino kennt. |
Das Spiel und viele Varianten werden in Buch 1 auf 200 Seiten
untersucht.
Trioker
selbst gemacht
Offenbar kann man das Troiker-Spiel aus 24 Steinen heute
nicht kaufen. Doch man kann die Dreiecke selbst herstellen. Man verwendet
die 20 Steine mit den Ziffern 0, 1, 2 oder 3 des Triomino-Spiels.
... ... ... |
Dann beschriftet man vier passende Papier-Dreiecke mit
021 031 032 und 132, schneidet in die Mitte ein kleines Loch und klebt
sie auf Steine, die eine 4 und 5 tragen.
Die Spielsteine haben in der Mitte Kuppen aus Metall,
die es ermöglichen, die Steine leichter anzuheben. |
Dann kann man versuchen,
Figuren wie oben nachzulegen.
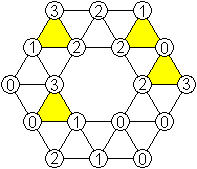
18 von 24
|
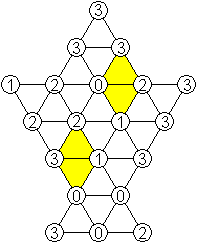
22 von 24
|
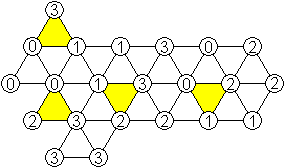
24 von 24
|
Trominos top
Heinz Haber beschreibt in Buch (1) ein Puzzle aus 24
Dreiecken und nennt es das Tromino-Spiel. Es gibt einen wesentlichen
Unterschied zum Spiel Troiker. Die Ziffern werden nicht den Ecken der Dreiecke
zugeordnet, sondern den Seiten. Dazu werden die Dreiecke in drei Teildreiecke
aufgeteilt.
| Das führt zu 24 Dreiecken. |
 |
Es werden die gleichen Tripel
wie bei Troiker verwendet, nämlich
000 001 002 003 011 012 013 022 023 033
111 112 113 122 123 133
222 223 233
333 |
+ 021 031 032 132 |
...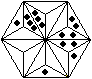 ... ... |
Ich will es bei diesem gelösten Sechseck belassen,
da sich die Figuren im nächsten Kapitel als farbige Figuren wiederholen
würden. |
Man könnte auch das
Triomino-Spiel mit den Ziffern 0 bis 5 um die symmetrischen Dreiecke erweitern.
000 001 002 003 004 005 011 012 013 014 015 022 023 024
025 033 034 035 044 045 055
111 112 113 114 115 122 123 124 125 133 134 135 144 145
155
222 223 224 225 233 234 235 244 245 255
333 334 335 344 345 355
444 445 455
555 |
+ 021 031 041 051
032 042 052
043 053 054
132 142 152
143 153 154
243 253 254 354 |
Dann kämen zu den 56 Triominos noch 20 Dreiecke hinzu.
Das macht 76 Steine.
Es stellt sich die Frage
nach einer allgemeinen Formel für die Anzahl a(n) der Dreiecke mit
n Ziffern.
Die Anzahl der zusätzlichen symmetrischen Dreiecke
wird durch "n über 3" oder C(n,3) angegeben. Dabei hält man sich
an den Term C(49,6) beim Lotto 6 aus
49.
Es gilt C(n,3)=n!/[3!*(n-3)!]=(1/6)n(n-1)(n-2).
Es gilt weiter a(n)=T(n)+C(n,3)=(1/6)n(n+1)(n+2) + (1/6)n(n-1)(n-2)=(1/3)n*(n²+2).
Es gilt a(4)=(1/3)*4*18=24 und a(6)=(1/3)*6*38=76, was
für die Formel spricht.
MacMahons Dreiecke
top
Der Name MacMahons Dreiecke weist auf Percy
Alexander MacMahon (1854 bis 1929) hin, der schon in den 1920er Jahren
auf die Möglichkeit hinwies, diese farbigen Dreiecke als Puzzlesteine
zu verwenden. Er untersuchte eher farbige Würfel (s.u.).
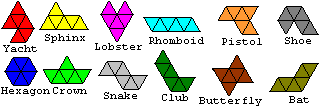
Martin Gardner machte die
24 Dreiecke zum Thema seiner Mathematik-Ecke der Zeitschrift Scientific
American. In einem Kapitel seines Buches (1) fasste er das Thema unter
Berücksichtigung zahlreicher Zuschriften zusammen.
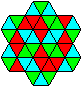
Es gibt einen unwesentlichen
Unterschied zum Tromino. Jede Ziffer wird durch eine Farbe ersetzt.
Ich wähle Rot 0, Grün 1, Blau 2 und Rot 3.
| Das führt zu 24 Dreiecken: |
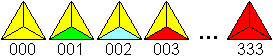 |
... ... ... |
Dann sieht das Sechseck links des Spiels
Tromino farbig so aus:
|
...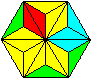 . . |
Immer, wenn Martin Gardner
ein Puzzle in einer Kolumne vorstellte, erhielt er viele Zuschriften mit
Anregungen und Lösungen. Ich stelle zwei bemerkenswerte Ergebnisse
vor.
...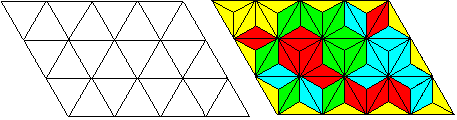 ... ... |
Es gibt 24 farbige Dreiecke.
Das zu 24=4*6 gehörige Parallelogramm kann man mit
Dreiecken auslegen und dabei sogar erreichen, dass der Rand gelb wird. |
...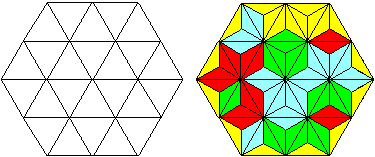 ... ... |
24 gleichseitige Dreiecke bilden ein regelmäßiges
Sechseck.
Man kann wieder erreichen, dass es ausgelegt wird und
der Rand gelb wird. |
Gardners Artikel ist eine Fundgrube für weitere Probleme.
Es ist wohl nicht möglich,
diese einfachen Figuren mit den Troiker-Steinen zu legen.
Ähnliche
Puzzles auf meiner Homepage top
Puzzle Wabe
Instant
Insanity
... ... ... |
...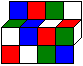 ... ... |
Aufgabe des Puzzles ist es, die Würfel so zu einer
1x1x4-Stange zusammenzustellen, dass auf allen vier Seitenflächen
die vier Farben erscheinen. |
MacMahons
Farbwürfel
... ...... ......
|
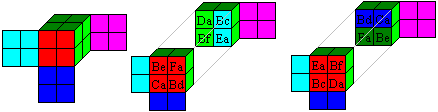
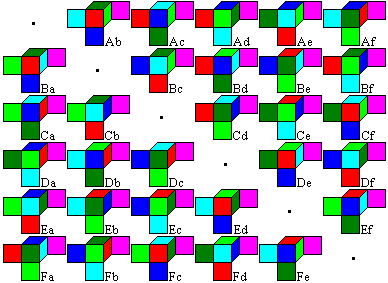
MacMahons Problem:
Baue einen 2x2x2 Würfel mit den gleichen Farben
auf den entsprechenden Seitenflächen wie ein Einzelwürfel.
Erschwerend kommt hinzu, dass innen gleiche Farben aufeinander
liegen.
|
Farbkontakt-Puzzle
Schlussbemerkung top
Ich habe auf dieser Seite das Triomino-Spiel aus 56 Steinen
in den Mittelpunkt gestellt, weil man es in jedem gut sortierten Spielzeugladen
kaufen kann. Da habe ich die Hoffnung, dass diese Seite "praxisnah" ist.
Trotzdem ist es als Puzzle aus zwei Gründen nicht ideal.
... ... ... |
>Mit 56 Steinen ist die Anzahl zu groß.
>Man vermisst die beiden jeweils zueinander symmetrischen
Dreiecke.
Oft scheiterte ich an einer Situation wie links. |
Die anderen Versionen des
Triomino-Spiels auf dieser Seite (Troiker, Tromino, MacMahons Farbdreiecke)
haben diese beiden Nachteile nicht. Nur über sie gibt es dann auch
eine gehaltvolle Literatur für Puzzle-Liebhaber (s.u.).
Triominos im Internet
top
Deutsch
Claudia Schlee & Andreas Keirat
Spieletest
für das Spiel : TRI-OMINOS
Jörg Binnewald
Zehnerbrüche
und Dezimalbrüche
Wikipedia
Triomino
(Spiel),
Domino
(Spiel)
Youtube
Spielerklärung
Triominos
Englisch
BoardGameGeek
Tri-ominos
Auf dieser Webseite wird erwähnt, dass man die 20
symmetrischen Spielsteine zum Triomino-Spiel als Extra Stones dazukaufen
kann.
Eric W. Weisstein (MathWorld)
Triomino
Wikipedia
Triomino
(game),
Dominoes (game)
Wikipedia
Triomino |
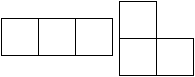
|
Das sind auch Triominos. |
Le
Trioker
Referenzen top
(1) Heinz Haber: Mathematisches Kabinett, dtv
10121, München 1967 und 1970 [ISBN 3-423-10121-0]
(2) M-Oldier, Y.Roussel: Troiker mathematisch gespielt,
Braunschweig 1979 [ISBN 3-528-08394-8]
(3) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont
taschenbuch1480) [ISBN 3-7701-2097-3]
(4) Martin Gardner: Mathematische Hexereien, Berlin 1988
[ISBN 3550065787]
Ferner:
(5) Major P.A.MacMahon: New Mathematical Pastimes, Cambridge
University Press, 1921
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
August 2012 Jürgen Köller
top |
|








 ...
... ...
... ...
... ...
... ...
...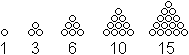




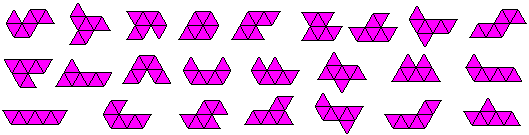 ...
...


 ...
...
 ...
... ...
... ...
... ...
... ...
... ...
...
 ...
...

 ...
...
 ...
...


 ...
...
 .
. ...
... ...
...
 ...
... ......
......


 ...
...