|
Was ist ein magisches Quadrat?
Das soll am magischen Quadrat auf Albrecht Dürers
Kupferstich
Melancholie von 1514 erklärt werden.
... .... ....
|
Man ordnet die Zahlen 1 bis 16 so zu einem Quadrat an,
dass die Summe der Zahlen untereinander, nebeneinander oder diagonal 34
ist.
Verwendet man als Zahlen 1 bis 16 wie hier, so erhält
man das normale magische Quadrat. |
Magische Quadrate und Varianten
sind schon seit alters her ein beliebtes Thema der Unterhaltungsmathematik.
Aus der Fülle des Angebots in Literatur und Internet habe ich das
zusammengetragen, was ich interessant finde.
Magische
Quadrate n-ter Ordnung top
Die Existenz magischer Quadrate ist für alle natürlichen
Zahlen n>2 gesichert. Es ist aber kein Bildungsgesetz für beliebige
Zahlen n bekannt. - Das sind Beispiele der kleinsten,
magischen Quadrate.
Die Seitenlänge heißt
auch Ordnung. Die Beispiele sind also magische Quadrate der Ordnungen 3,
4, 5, 6, 7 und 8.
Allgemein definiert man:
Ein Quadrat n-ter Ordnung ist magisch, wenn die Zahlen
1, 2, 3, ... , n² so in einem n x n-Quadrat verteilt werden, dass
die Summen der n Zahlen untereinander, nebeneinander oder diagonal konstant
sind. Die Summe heißt magische Zahl.
Es gilt (1+2+3+...+n²):n = (1/2)n(n²+1).
Und das sind die magischen Summen der ersten acht Quadrate.
Magisches Quadrat:
Magische Summe: |
3x3
15
|
4x4
34
|
5x5
65
|
6x6
111
|
7x7
175
|
8x8
260
|
9x9
369
|
10x10
505
|
Das
magische 3x3-Quadrat
Es gilt 1+2+3+4+5+6+7+8+9=45. Beim magischen Quadrat
werden jeweils 3 Zahlen addiert. Also ist die mittlere Summe dreier Zahlen
gleich 45:3=15.
Man kann auch auf die magische Zahl 15 kommen, wenn man
den mittleren Summanden 5 dreimal addiert.
Die Zahl 15 lässt sich achtmal in eine Summe aus
drei Summanden zerlegen:
15=1+5+9
15=1+6+8
|
15=2+4+9
15=2+5+8
|
15=2+6+7
15=3+4+8
|
15=3+5+7
15=4+5+6
|
In den Zerlegungen kommen die ungeraden Zahlen 1,3,7 und
9 zweimal vor, die geraden Zahlen 2,4,6 und 8 dreimal, und die Zahl 5 erscheint
viermal.
Daraus folgt, dass man die Zahl 5 in die Mitte eines
magischen 3x3-Quadrates setzen muss. Die übrigen ungeraden Zahlen
muss man in die Seitenmitten und die geraden Zahlen in die Ecken setzen.
Es gibt unter diesen Bedingungen acht Möglichkeiten
ein Quadrat zu bilden:
...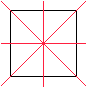 ... ... |
Alle acht Quadrate gehen ineinander über, wenn man
sie an ihren Symmetrieachsen spiegelt.
Das sind die Diagonalen und die Mittellinien.
Symmetrische Quadrate dieser Art zählt man nur einmal. |
Es gibt unter diesem Gesichtspunkt
nur ein magisches 3x3-Quadrat.
Varianten
der 3x3-Quadrate
top
Nicht-normale magische Quadrate
...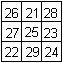 ... ... |
Die Zahlen 21 bis 29 bilden ein magisches Quadrat mit
der magischen Summe 75. |
Die Erklärung ist einfach.
........6+c....1+c....8+c........
........7+c....5+c....3+c........
........2+c....9+c....4+c........ |
Ein magisches Quadrat bleibt nämlich magisch, wenn
man jede Zahl mit einer Konstanten c verändert, zum Beispiel durch
Addition von c zu jeder Zahl. Oben ist c=20.
Man kann auch subtrahieren, multiplizieren oder dividieren. |
Quadrat aus
Primzahlen
...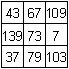 ... ... |
Das ist ein magisches Quadrat aus Primzahlen................................................................................. |
Quadrat
aus Quadratzahlen
...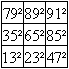 ... ... |
Das ist ein "semi"-magisches Quadrat aus Quadratzahlen.
Nur die Summen durch den Mittelpunkt sind gleich................................................................ |
Quelle: http://www.mathpages.com/home/kmath417.htm
Das magische
Multiplikationsquadrat
Das ist ein magisches Quadrat, bei dem nicht die Summen,
sondern die Produkte aus den Zahlen in den Zeilen, Spalten und Diagonalen
gleich sind.
Es gibt eine einfache Bildungsregel.
... ... ... |
...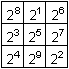 ... ... |
Man geht z.B. von dem magischen 3x3-Quadrat aus und ersetzt
die Zahlen durch Zweierpotenzen mit ihnen als Hochzahlen.
Das magische Produkt ist 215=32768. |
...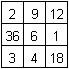 ... ... |
Dieses 3x3-Quadrat ist das Quadrat mit dem kleinsten
Produkt.
Das magische Produkt ist 216. |
Das magische
4x4-Quadrat top
Zerlegungen der magischen Zahl
Die magische Zahl ist (1+2+...+15+16):4 = 34.
Der Computer fand 86 Zerlegungen von 34 in eine Summe
von vier Summanden aus den Zahlen 1 bis 16:
34=01+02+15+16
34=01+03+14+16
34=01+04+13+16
34=01+04+14+15
34=01+05+12+16
34=01+05+13+15
34=01+06+11+16
34=01+06+12+15
34=01+06+13+14
34=01+07+10+16
34=01+07+11+15
34=01+07+12+14
34=01+08+09+16
34=01+08+10+15
34=01+08+11+14
34=01+08+12+13
34=01+09+10+14
34=01+09+11+13 |
34=01+10+11+12
34=02+03+13+16
34=02+03+14+15
34=02+04+12+16
34=02+04+13+15
34=02+05+11+16
34=02+05+12+15
34=02+05+13+14
34=02+06+10+16
34=02+06+11+15
34=02+06+12+14
34=02+07+09+16
34=02+07+10+15
34=02+07+11+14
34=02+07+12+13
34=02+08+09+15
34=02+08+10+14
34=02+08+11+13 |
34=02+09+10+13
34=02+09+11+12
34=03+04+11+16
34=03+04+12+15
34=03+04+13+14
34=03+05+10+16
34=03+05+11+15
34=03+05+12+14
34=03+06+09+16
34=03+06+10+15
34=03+06+11+14
34=03+06+12+13
34=03+07+08+16
34=03+07+09+15
34=03+07+10+14
34=03+07+11+13
34=03+08+09+14
34=03+08+10+13 |
34=03+08+11+12
34=03+09+10+12
34=04+05+09+16
34=04+05+10+15
34=04+05+11+14
34=04+05+12+13
34=04+06+08+16
34=04+06+09+15
34=04+06+10+14
34=04+06+11+13
34=04+07+08+15
34=04+07+09+14
34=04+07+10+13
34=04+07+11+12
34=04+08+09+13
34=04+08+10+12
34=04+09+10+11
34=05+06+07+16 |
34=05+06+08+15
34=05+06+09+14
34=05+06+10+13
34=05+06+11+12
34=05+07+08+14
34=05+07+09+13
34=05+07+10+12
34=05+08+09+12
34=05+08+10+11
34=06+07+08+13
34=06+07+09+12
34=06+07+10+11
34=06+08+09+11
34=07+08+09+10
.
.
.
. |
In den Zerlegungen von 34 sind die Summanden 1 bis 16 etwa
gleichmäßig verteilt.
Summand:
Anzahl: |
01
19 |
02
20 |
03
21 |
04
22 |
05
22 |
06
23 |
07
23 |
08
22 |
09
22 |
10
23 |
11
23 |
12
22 |
13
22 |
14
21 |
15
20 |
16
19 |
Im Unterschied zum 3x3-Quadrat kann man daraus kaum Schlüsse
auf die Verteilung der Zahlen 1 bis 16 im 4x4-Quadrat ziehen.
Muster
im Dürer-Quadrat
... .... ....
|
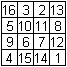
Wie oben erwähnt ist im Deutschen das magische Quadrat
von Dürer das magische Quadrat schlechthin. |
...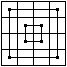 ... ... |
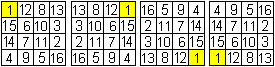
Markiert man vier Zahlen mit der Summe 34, so liegen
sie oft symmetrisch im Quadrat verteilt und bilden einfache Figuren wie
die Quadrate links. |
In Buch (7) findet man 28 Figuren, die symmetrisch sind
und auch symmetrisch bzgl. von Achsen des Quadrates liegen.

10 Strecken
|

4 Quadrate
|

2 Rauten
|

4 Rechtecke
|

8 Parallelogramme
|
Ich habe mich gefragt, welche
Muster die 86 Zerlegungen der Zahl 34 bilden.
Dazu werden die 86 Zerlegungen mit Computerhilfe graphisch
dargestellt.
Ordnet man die Figuren, so
ergeben sich z.B. vier Klassen.
Standard
... .. .. |
Da sind zuerst einmal die 28 symmetrischen Figuren von
oben aus Buch (7)................................... |
Achtfach
... ... ... |
Eine Figur tritt 8x auf. ....................................................................................................................... |
Vierfach
... ... ... |
Acht Figuren treten 4x auf. Sie sind bis auf eine Ausnahme
symmetrisch.............................
Das sind insgesamt 32 Figuren. |
Doppelt
... ...... ...... |
9 Figuren treten doppelt auf. Sie sind asymmetrisch.
Das sind insgesamt 18 Figuren........................................................................................................................... |
Kontrolle: 28+8+32+18=86
Mehr über das Ordnen
dieser Figuren findet man auf der Webseite von Harvey Heinz Order 4
Magic Squares
(URL unten).
Konstruktion
eines 4x4-Quadrates
Es gibt eine einfache Möglichkeit, ein magisches
4x4-Quadrat zu erzeugen.
... ............. ............. |
>Schreibe die Zahlen von 1 bis 16 Zeile für Zeile
in das Quadrat. |
...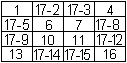 ... ... |
>Lasse die Zahlen in den Ecken und im mittleren 2x2-Quadrat
stehen.
Ersetze die übrigen Zahlen n durch 17-n. |
... ... ... |
Es ist ein magisches Quadrat entstanden..... |
Quelle: (1) Seite 134
Achsensymmetrische
magische Quadrate
Man erhält neue Quadrate,
indem man an den vier Achsen des Quadrates spiegelt.
Wie beim magischen 3x3-Quadrat sieht man die acht Varianten
als gleich oder äquivalent an.
Man weiß: Es gibt insgesamt
880 magische 4x4-Quadrate.
Dabei werden die eben vorgestellten achsen- und zugleich
punktsymmetrischen Quadrate nur einmal gezählt.
Punktsymmetrisches
magisches Quadrat
... ... ... |
Bilden die beiden zum Mittelpunkt punktsymmetrisch zueinander
liegende Zahlen die Summe n²+1=17, so heißt das magische Quadrat
punktsymmetrisch oder selbstkomplementär.
Die Ersetzung aller Zahlen n durch 17-n bedeutet eine
Drehung um 180°. |
Das Dürer-Quadrat ist punktsymmetrisch.
Halbmagisches Quadrat
Ein Zahlenquadrat heißt halbmagisch,
wenn nur
die Summe der Zahlen untereinander und nebeneinander die
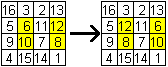
magische Zahl ist. Man kann das Dürer-Quadrat leicht so abändern,
dass die Summe der Zahlen in den Diagonalen nicht mehr 34 ist.
... ... ...
|
Dazu tauscht man wie links zwei untereinanderliegende
Paare mit gleicher Summe aus. Die Zahlen 6 und 10 liegen auf Diagonalen
und stören die Summen. Aus 34 und 34 wird 30 und 38. |
Magisches
Parkett
...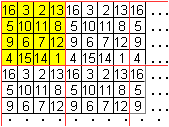 ... ... |
Ein halbmagisches Parkett entsteht, wenn man ein beliebiges
magisches Quadrat (z.B. das Dürer-Quadrat) auswählt und nebeneinander
und untereinander wiederholt. |
...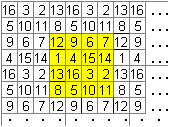 ... ... |
Dann ist jedes Quadrat aus 16 Zahlen halbmagisch......................................................................... |
... ... ... |
Hat das parkettbildende Quadrat noch die zusätzliche
Eigenschaft, dass die Summen der "gebrochenen" Diagonalen auch noch den
Wert der magischen Zahl haben, so heißt es panmagisch. |
...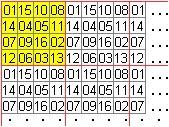 ... ... |
Ein magisches Parkett entsteht, wenn man ein panmagisches
Quadrat wählt und nebeneinander und untereinander wiederholt. |
...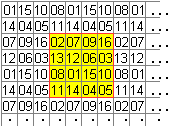 ... ... |
Jedes Quadrat aus16 Zahlen, das man in des Feld legen
kann, ist magisch...................................... |
(8), Seite 253ff.
"Antimagisches"
Quadrat
... ... ... |
Alle Summen in den Zeilen, in den Spalten und in den
Diagonalen sind voneinander verschieden (4). |
Das magische
5x5-Quadrat top
Die magische Zahl ist (1+2+...+24+25) : 5 = 65.
Zerlegungen
der magischen Zahl 65
65 = 01+02+13+24+25
65 = 01+02+14+23+25
65 = ...
65 = ... |
65 = ...
65 = ...
65 = 10+12+13+14+16
65 = 11+12+13+14+15 |
Der Computer fand 1394 Zerlegungen der Zahl 65. |
Die Summanden und ihre Anzahl in den Summen:
Es fällt auf, dass der mittleren Zahl 13 = 65:5 die
größte Anzahl zugeordnet ist.
Die Anzahl der Summanden zu größer und kleiner
werdenden Summanden nimmt beidseitig symmetrisch ab.
Man weiß: Es gibt 275 305 224
magische 5x5-Quadrate. (Scientific American 1/1976, deutsche Ausgabe)
Konstruktion
eines magischen 5x5-Quadrats
Die Zahlen 1 bis 25 werden der Reihe nach auf die Felder
verteilt. Dabei werden für die nächste Zahl die Regeln "weiter
oben rechts" und "falls besetzt, darunter weiter" beachtet.
..................... .................... .................... |
Die Zahl 1 kommt in die
Mitte der ersten Zeile.
Die nächste Zahl 2
folgt oben rechts. Aber dann verlässt man das Feld.
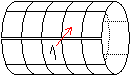 Deshalb muss man sich das Quadrat als einen Zylinder denken.
Der Zylinder hat die vertikalen Seiten als Kreisumfänge, die horizontalen
Seiten stoßen aufeinander und schließen den Mantel des Zylinders.
Dann ist oben rechts ein Platz für die 2. Wieder auseinandergerollt
ist die Zahl 2 in die letzte Zeile ein Feld nach rechts gewandert.
Deshalb muss man sich das Quadrat als einen Zylinder denken.
Der Zylinder hat die vertikalen Seiten als Kreisumfänge, die horizontalen
Seiten stoßen aufeinander und schließen den Mantel des Zylinders.
Dann ist oben rechts ein Platz für die 2. Wieder auseinandergerollt
ist die Zahl 2 in die letzte Zeile ein Feld nach rechts gewandert. |
Zahl 3 folgt oben rechts.
...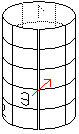 ... ... |
Die Zahl 4 würde wieder
außerhalb des Feldes liegen. Man denkt sich wieder einen Zylinder,
dieses Mal mit vertikaler Achse. Man kann dann die Zahl 4 wieder oben rechts
unterbringen. Auseinandergerollt liegt die Zahl in der dritten Zeile ganz
links. |
Die Zahl 5 liegt oben rechts.
Für die Zahl 6 wird
eine zweite Regel angewandt: Ist das Feld oben rechts besetzt, so gelangt
die nächste Zahl eine Zeile tiefer in die gleiche Spalte.
Man fährt mit 7,8
usw. fort. Für die Zahl 16 wird übrigens
die gleiche Regel wie für die Zahl 6 angewandt.
Dieses Bildungsgesetz lässt
sich auf alle magische Quadrate mit ungerader Seitenzahl übertragen
:-).
Zusammengesetzte
Quadrate top
Rahmenquadrate
... ... ... |
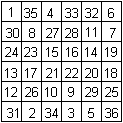
Das 7x7-Quadrat hat die magische Zahl 175.
Es enthält zwei weitere magische Quadrate.
Das 5x5-Quadrat hat die magische Zahl 125=5*12+65.
Das 3x3-Quadrat hat die magische Zahl 75=3*20+15. |
(1), Seite 154
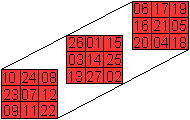
Magisches
Quadrat 9x9 mit magischen Teilquadraten
...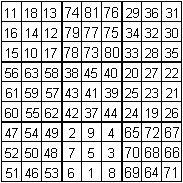 ... ... |
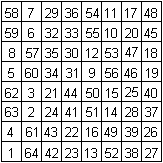
Das 9x9-Quadrat hat die magische Zahl 369.
Es setzt sich aus neun magischen 3x3-Quadraten zusammen.
Die magischen Zahlen sind
9+8
9+54
9+45 |
9+72
9+36
9+0 |
9+26
9+18
9+63 |
(1), Seite 156 |
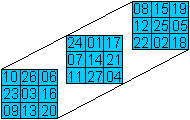
Magisches
Quadrat 8x8 mit magischen Teilquadraten
...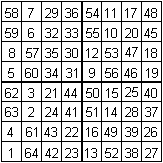 ... ... |
Das 8x8-Quadrat hat die magische Zahl 260.
Es setzt sich aus vier magischen 4x4-Quadraten zusammen.
Alle vier magischen Quadrate haben die magische Zahl 130.
(1), Seite 155
|
Besondere
Quadrate top
Lateinisches Quadrat
.... .. .. |
Auch hier sind die acht Summen im Quadrat konstant.
Es werden allerdings nur die ersten drei Zahlen verwandt.
Lateinische Quadrate gibt es allgemein für die n-te
Ordnung. |
Magic
21 Square
... ... ... |
Das ist ein Schiebepuzzle nach Art des Fünfzehnerspiels.
In den fünf Zeilen und den fünf Spalten ist
die Summe 21.
Ziel des Puzzles ist es, die Steine so zu verschieben,
dass auch in den Diagonalen die Summe 21 wird.
©
2008 Taquinze (Hans Janmaat) |
Sudoku
... ... ... |
 ... ... |
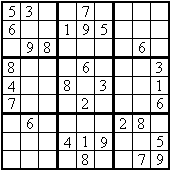
Von den lateinischen Quadraten
ist es ein kleiner Schritt zum Sudoku. |
Magische
Buchstaben-Quadrate
...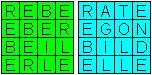 ... ... |
Diese und ähnliche magische Quadrate aus Buchstaben
kennt man aus Rätselecken von Zeitschriften.
Die Buchstaben bilden sinnvolle Wörter. |
Ein bekanntes Quadrat dieser
Art ist das Sator-Quadrat, zu dem es eine Wikipedia-Seite gibt (URL unten).
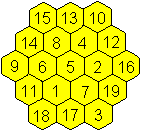
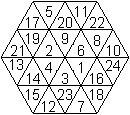
Magischer Würfel
top
...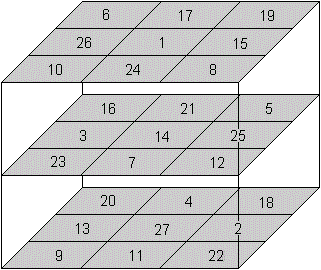 ... ... |
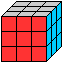
Der magische Würfel dritter Ordnung ist eine Verallgemeinerung
des magischen 3x3-Quadrates.
Die Zahlen 1 bis 27 werden so auf die Felder eines 3x3x3-Würfels
verteilt, dass die Summen
>der Zahlen der 18 Zeilen,
>der Zahlen der 9 Spalten
>der Zahlen der 4 Raumdiagonalen konstant sind.
Die magische Zahl ist 42. |
Auf eine Eigenschaft muss verzichtet werden: Die Summe der
Zahlen der 18 Flächendiagonalen ist nicht 42.
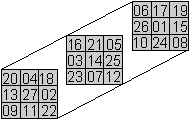
Andere Sichtweise
Der magische Würfel enthält neun verschiedene
halbmagische Quadrate.
Längs der vier Raumdiagonalen
liegen die folgenden Summen.
| 09+14+19=42 |
22+14+06=42 |
20+14+08=42 |
18+14+10=42 |
(3), Seite 142f.
Keine Quadrate mehr
top
Einfache Varianten mit magischer
Summe
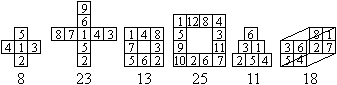
Magisches
Rechteck
... |

|
Das 2x4-Rechteck hat die magischen Zahlen 9 und 18.
Das 4x8-Rechteck hat die magischen Zahlen 66 und 132.
(1), Seite 156 |
Magische
Pythagoras-Figur
...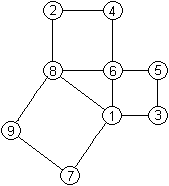 ... ... |
25² =20²+15² lässt sich schreiben
als (1+8+9+7)² = (6+4+2+8)²+(5+3+6+1)².
Diese Rechnung veranschaulicht man, indem man die Zahlen
1 bis 9 auf die Ecken der Pythagoras-Figur verteilt. |
(3), Seite 143
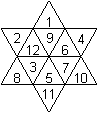
Magischer
fünfeckiger Stern
...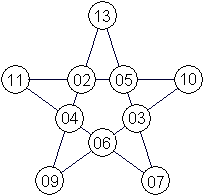 ... ... |
Der magische Fünfeck-Stern enthält zehn viergliedrige
Summen mit der magischen Zahl 28.
Es werden von den ersten 13 Zahlen 10 Zahlen verwendet
(8), Seite 213. |
Offenbar gibt es keinen normalen magischen Stern der Ordnung
5.
Magisches
Sechseck und Varianten
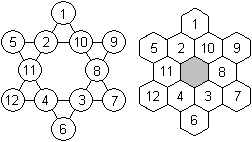
Auf meiner Webseite Magisches
Sechseck findet man unterschiedliche magische Figuren in Sechseckform,
darunter auch magische Sterne.
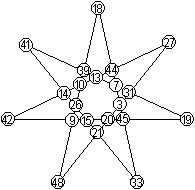
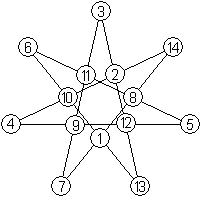
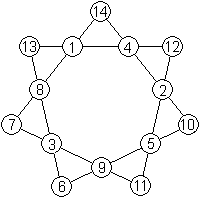
Magischer
siebeneckiger Stern
Zwei normale magische Sterne mit der magischen Summe
30.
Quelle: Homepage von Harvey D. Heinz (URL unten)
... |
Vollständiger magischer Stern
Verwendet werden 21 Zahlen aus der Menge {3, 4, 5, ...,
46, 47, 48}.
Die magische Summe ist 150.
(7) Seite 24 |
Der
magische Kreis
...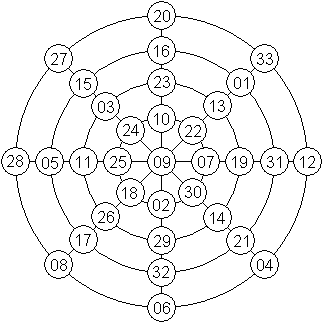 ... ... |
Der magische Kreis enthält 4+8=12 achtgliedrige
Summen.
Die Summe auf jedem Kreis ist 138.
Die Summe auf jedem Durchmesser (die 9 in der Mitte ist
zu streichen) ist ebenfalls 138.
Nach (7) wurde er 1275 vom Chinesen Yang Hui entworfen. |
Magische
Quadrate im Internet top
Deutsch
Christoph Pöppe (Spektrum der Wissenschaft - Dossier)
Edle magische
Quadrate
Felix Kunert & Karsten Lehmann (raetselverzeichnis.de)
Magisches
Quadrat Rätsel
Gerd Müller
Magisches
Quadrat interaktiv
Hans-Peter Gramatke
Magische
Quadrate
H.B. Meyer
magische Quadrate: 4
x 4, 5 x 5,
6
x 6
Holger Danielsson
Magische Quadrate
Jan Theofel und Martin Trautmann
Magische
Quadrate und Würfel
Maria Koth
Magische
Quadrate (.pdf.-Datei)
Paul Heimbach
Magische Quadrate
recordholders.org
Das
größte Magische Quadrat der Welt
Udo Hebisch (Mathematisches Café)
Magische
Quadrate
Wikipedia
Magisches
Quadrat, Vollkommen
perfektes magisches Quadrat, Sator-Quadrat,
Magischer
Würfel,
Lateinisches
Quadrat, Hexeneinmaleins
Englisch
Craig Knecht (Magic
Square Models)
|
...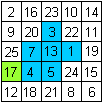 ... ... |
Man stelle sich vor: Die Quadrate sind die Spitzen quadratischer
Prismen der Höhe der Zahlenangaben. Schüttet man Wasser auf diesen
Körper, so bleibt es in der Mitte bis zur Höhe 17 als Teich stehen.
Da fließt es ab. Die Wassermenge ist (17-3)+(17-7)+(17-13)+(17-1)+(17-4)+(17-5)=69.
Es gibt schöne Probleme: Größte Wassermenge?
Getrennte Seen? Inseln?
Water
Retention Patterns |
...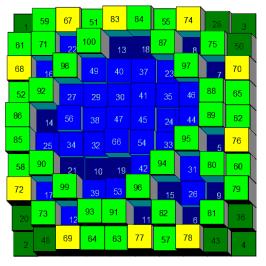 ... ... |
Das nächste Bild zeigt anschaulich, was unter Water
Retention Patterns zu verstehen ist.
Man findet Programme dazu auf der Webseite http://users.eastlink.ca/~sharrywhite/Download.html
(nicht mehr online) |
Eric W. Weisstein (MathWorld)
Magic
Square,
Panmagic
Square,
Associative
Magic Square, Lo
Shu, Prime
Magic Square, Magic
Cube, Magic
Circles
Harvey D. Heinz
Magic Hypercubes
Home Page,
Order
4 Magic Squares
H.B. Meyer
magic squares: 4
x 4, 5 x 5,
6
x 6
Holger Danielsson
Magic
Squares
Mark S. Farrar
Magic
Squares
MathPages
Solving
Magic Squares
Robin Moseley
Magic
Flexagon (.pdf-File)
The
On-Line Encyclopedia of Integer Sequences
magic
numbers, sequences related to ..., Sequence of magic numbers:
A006003
Wikipedia
Magic
square,
Most-perfect
magic square, Sator
Square, Magic
cube, Magic star,
Simple
magic cube,
Latin
square,
Magic
circle (mathematics), Water
retention on mathematical surfaces, Associative
magic square
Referenzen
top
(1 ) Hermann Schubert: Mathematische Mußestunden,
Berlin 1941 (Erstauflage )
(2) Wilhelm Ahrens: Mathematische Unterhaltungen und
Spiele, Leipzig 1901
(3) Walter Lietzmann: Lustiges und Merkwürdiges
von Zahlen und Formen, Göttingen 1969
(4) Bild der Wissenschaften, 8/1966, 6/1968, 7/1971,
9/1971, 3/1974, 10/1976
(5) Pieter van Delft /Jack Botermans: Denkspiele der
Welt, München 1980 (1998 neu aufgelegt)
(6) Maximilian Miller: Gelöste und ungelöste
mathematische Probleme, Leipzig 1982
(7) Kenneth Kelsey: Magische Zahlenspiele, dtv 1983 [ISBN
3-423-10199-7]
(8) Jan Gullberg: Mathematics - From the Birth of Numbers,
New York - London 1997 (ISBN0-393-04002-X)
(9) Tibor Bakos: Magische Quadrate, in "Mathematisches
Mosaik", Köln 1977 [ISBN 3-7614-0371-2]
Feedback: Emailadresse auf meiner Hauptseite
Die 2011 überarbeitete Seite
ist nicht in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |

 ....
....



 ...
... ...
... ...
...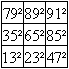 ...
...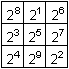 ...
... ...
... ...
...




 ..
..  ...
... ...
... ......
...... .............
............. ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ....................
....................
 ...
... ...
... ...
... ...
... ..
.. ...
... ...
... ...
...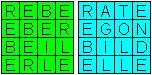 ...
... ...
...

 ...
... ...
...

 ...
... ...
... ...
...