|
Was ist ein Deltaeder?
Ein Deltaeder ist ein Körper, dessen Seitenflächen
gleichseitige Dreiecke sind.
Der Name geht auf den großen griechischen Buchstaben
Delta zurück, der die Dreiecksform hat.
... |
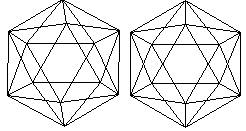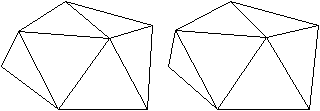
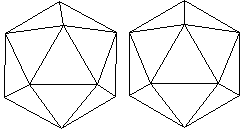
Ein bekannter Körper dieser Art ist das Ikosaeder
mit seinen 20 Seitenflächen.
Man sieht es dreidimensional, wenn man den 3D-Blick beherrscht. |
Es gibt unendlich viele Deltaeder. Man denke daran, dass
man beliebig viele Tetraeder aneinander legen kann.
Auf dieser Seite beschränke ich mich auf die acht
konvexen Deltaeder. Sie sind - anschaulich ausgedrückt - nur nach
außen gewölbt.
Diese Deltaeder werden der
Reihe nach besprochen. Sie werden nach der Anzahl der Seitenflächen
geordnet.
01 Tetraeder top
...
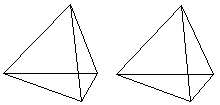
...durchsichtig |
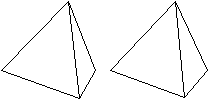
undurchsichtig |
4
|
Das Tetraeder hat 4 Ecken, 6
Kanten und 4 Seitenflächen und gehört
zu den platonischen Körpern.
Mehr darüber erfährt man auf meiner
Tetraeder-Seite.
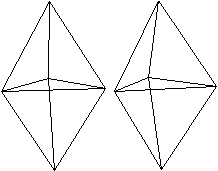
02 Triangulare
Bipyramide top
... ... |
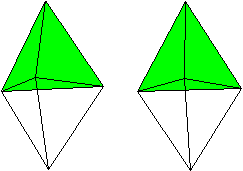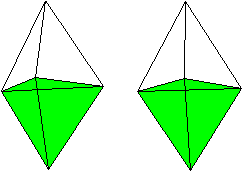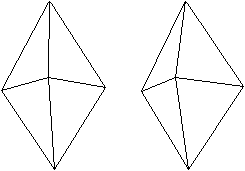
Wie der Name sagt entsteht dieser
Körper, indem man das Tetraeder an der Grundfläche spiegelt. |
Die triangulare Bipyramide
hat 5 Ecken, 9 Kanten und 6 Seitenflächen.
Sie gehört zu den 92 konvexen Körpern mit regulären
Flächen, die Norman M. Johnson katalogisiert hat, den Johnson-Körpern.
Sie trägt die Nummer 12 und wird mit J 12 bezeichnet.
03 Oktaeder top
Man kann das Oktaeder als quadratische
Bipyramide oder als Antiprisma
mit gleichseitigen Dreiecken als Grundseiten ansehen.
... |
 |
Das Oktaeder mit 6 Ecken, 12
Kanten und 8 Seitenflächen gehört
zu den platonischen Körpern.
Mehr darüber erfährt man auf meiner
Oktaeder-Seite.
04 Pentagonale
Bipyramide top
... ... |
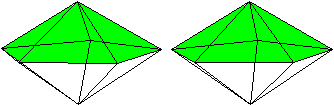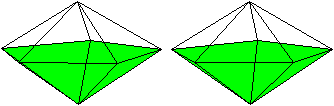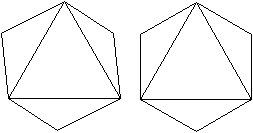
Wie der Name sagt entsteht dieser
Körper, indem man die regelmäßige fünfseitige
Pyramide an der Grundfläche spiegelt. |
Er
hat 7 Ecken, 15 Kanten und 10 Seitenflächen.
Er gehört zu den 92 Johnson-Körpern und wird
mit J 13 bezeichnet.
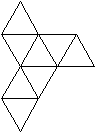
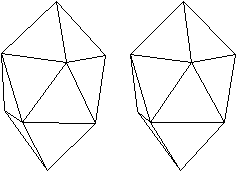
05 Trigondodekaeder
top
... |
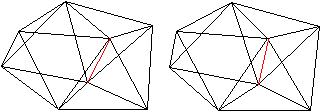Zeichnet man eine rote Linie ein, so liegt links ein
Oktaeder, rechts lehnen sich drei Tetraeder an. Die Körper sind aber
nicht regelmäßig, sondern verbogen. |
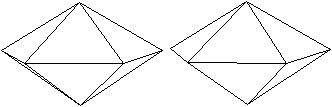
Einen
anderen Zugang bekommt man so.
... |
... |
|
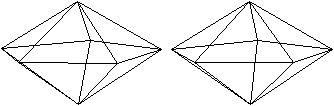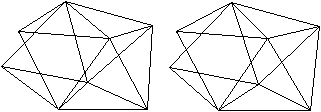Man geht aus von der fünfseitigen Bipyramide J 13 aus.
Dann öffnet man an der linken Ecke die Bipyramide wie eine Auster,
wobei zwei neue Kanten der Bipyramide auftreten. Dann verbindet man die
beiden freien Ecken links.
Dieser Körper hat 8 Ecken, 18 Kanten
und 12 Seitenflächen.
Er gehört zu den 92 Johnson-Körpern mit der
Bezeichnung J 84.
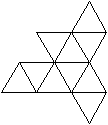
06
Dreifach erweitertes Dreiecksprisma top
... ... |
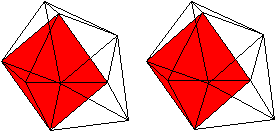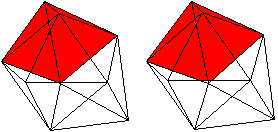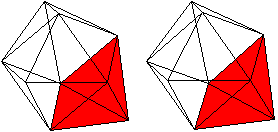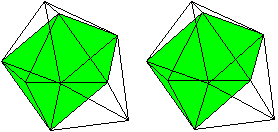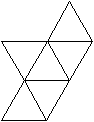
Der Körper besteht aus einem Dreiecksprisma (grün),
auf dessen drei Quadrate quadratische Pyramiden (rot) aufgesetzt werden. |
Er hat 9 Ecken, 21 Kanten und
14
Seitenflächen.
Er gehört zu den 92 Johnson-Körpern mit der
Bezeichnung J 51.
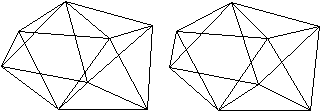
07
Zweifach erweitertes Antiprisma top
... ...
|
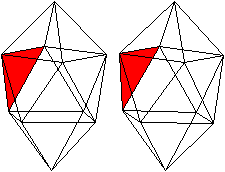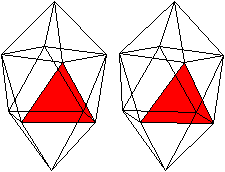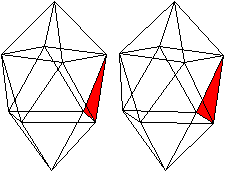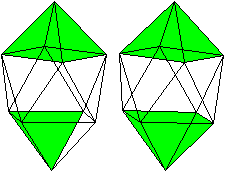
Der Körper hat acht gleichseitige Dreiecke (rot)
, die zu einem Antiprisma gehören.
Auf das Antiprisma werden zwei quadratische Pyramiden
(grün) gesetzt. |
Der Körper hat 10 Ecken,
24 Kanten, und 16 Seitenflächen.
Er gehört zu den 92 Johnson-Körpern mit der
Bezeichnung J 17.
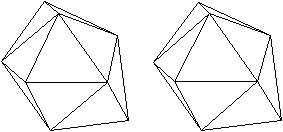
08 Ikosaeder top
... ... |
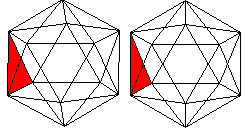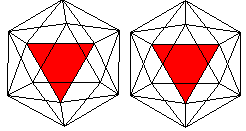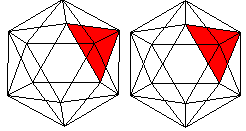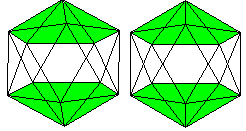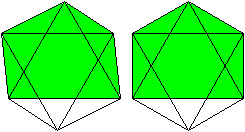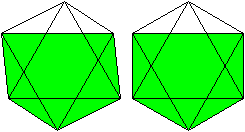
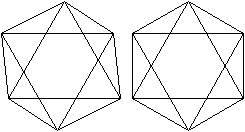
Man kann das Ikosaeder als fünfseitiges Antiprisma
mit zwei aufgesetzten Pyramiden ansehen. |
Das Ikosaeder hat 12 Ecken,
30 Kanten, und 20 Seitenflächen und gehört zu den platonischen
Körpern.
Mehr über diesen Körper erfährt man auf
meiner Ikosaeder-Seite.
Sonstiges top
Kanten und Seitenflächen
Es sei k die Anzahl der Kanten und f die der Seitenflächen.
Dann gilt für ein Deltaeder die Formel 2k = 3f.
Das sieht man so ein.
- Jedes Dreieck hat drei Kanten. Das führt zu f
= 3k.
- Da zwei nebeneinander liegende Dreiecke eine Kante
gemeinsam haben, muss man die Anzahl noch halbieren: f=(2k)/3.
Die Beziehung 2k = 3f findet
man in den einzelnen Deltaedern wieder.
Tetraeder
k=6, f=4
|
J12
k=9, f=6
|
Oktaeder
k=12, f=8
|
J13
k=15, f=10
|
J84
k=18, f=12
|
J51
k=21, f=14
|
J17
k=24, f=16
|
Ikosaeder
k=30, f=20
|
Die Gleichung f = (2k)/3
enthält auch die Aussage, dass die Anzahl der Seitenflächen gerade
ist.
Diese Beziehung findet man in der folgenden Tabelle.
Es fehlt f=18.
Ecken
eines Deltaeders
Man kann nur aus drei, vier oder fünf Dreiecke eine
Ecke formen. Man braucht nämlich mindestens drei Dreiecke für
eine Ecke und sechs Dreiecke haben schon zusammen 360° und liegen somit
in einer Ebene. Also bleiben nur 3, 4 und 5 Dreiecke.
Die Dreiecke bilden eine unten offene Pyramide.
Ist a die Grundseite, so haben die Pyramiden die folgenden
Höhen h.
Dreiseitige Pyramide
h=(1/3)sqrt(6)a
gerundet h=0,816a
|
quadratische Pyramide
h=(1/2)sqrt(2)a
gerundet h=0,707a
|
fünfeckige Pyramide
h=(1/10)sqrt[75-10*sqrt(5)]a
gerundet h=0,726a
|
Wie oft die drei Pyramiden
in den Körpern auftreten, entnimmt man der folgenden Tabelle.
Tetraeder
4*3 Kanten
|
J12
3*4 und 2*3
|
Oktaeder
6*4
|
J13
2*5 und 5*4
|
J84
4*5 und 4*3
|
J51
6*5 und 3*4
|
J17
8*5 und 2*4
|
Ikosaeder
12*5
|
Volumen
Es sei a die Kantenlänge eines Deltaeders. In der
folgenden Tabelle stehen die Formeln für die Volumina, darunter die
gerundeten Werte.
| Tetraeder
V = (1/12)sqrt(2)a³
V = 0,118a³ |
J12
V = (1/6)sqrt(2)a³
V = 0,236a³ |
Oktaeder
V = (1/3)sqrt(2)a³
V = 0,471a³ |
J13
V = (1/12)[5+sqrt(5)]a³
V = 0,603a³ |
Aus der Rolle fällt die Formel für das Volumen
des Trigondodekaeder J 84.
Das Volumen ist die positive reelle Lösung der Gleichung
5832V6-1377V4-2160V2-4 = 0.
Gerundet ist der Wert V = 0,859a³.
| J51
V = (1/4)[2sqrt(2)+sqrt(3)]a³
V = 1,140a³ |
J17
V = (1/3){sqrt(2)+sqrt[4+3sqrt(2)]}a³
V = 1,428a³ |
Ikosaeder
V = (1/12)[15+5sqrt(5)]a³
V = 2,182a³ |
Quelle: Eric W. Weisstein (MathWorld) (URL unten)
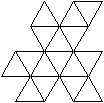
Übersicht
Zum Schluss zeigen sich die acht konvexen Deltaeder noch
einmal in der Aufsicht.
Weitere Deltaeder top
Boot
... ... |
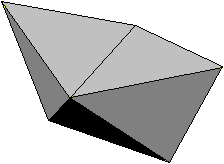Oben wurde schon erwähnt,
dass man weitere Deltaeder erhält, wenn man Tetraeder aneinander legt.
Drei Tetraeder bilden ein Boot.
Merkwürdig ist, dass es das gleiche Netz wie das Oktaeder hat. |
Hypertetraeder
... ... |
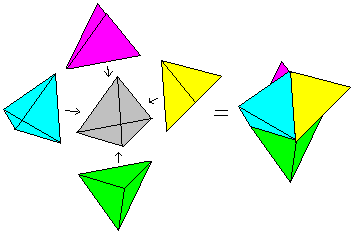Fünf Tetraeder bilden ein "Netz" des vierdimensionalen
Tetraeders, des Hypertetraeders. |
Sterntetraeder
... ...
|
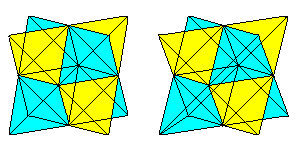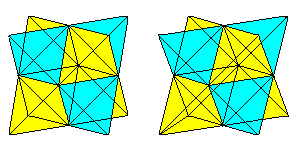Setzt man auf die Seitenflächen
des Oktaeders acht Tetraeder, so entsteht das Sterntetraeder mit acht Zacken. |
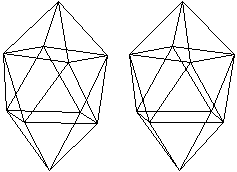
Bekrönte
Deltaeder
... ... |
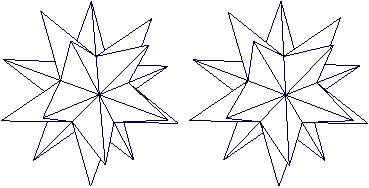Setzt man auf ein Ikosaeder 20 Tetraeder, so entsteht
ein Stern mit 60 Seitenflächen.
Die Firma Wolfram Research hat ihn zu ihrem Logo gewählt
(URL unten).
Statt des Ikosaeders kann man viele Deltaeder "bekrönen".
Der Stern links hat allerdings schlankere Zacken, da das
regelmäßige Fünfeck Grundlage ist. Der Körper heißt
Großes Sterndodekaeder
und gehört zu den
Kepler-Poinsot
Körpern. |
Deltaeder mit Vertiefungen
Verbindet man den Mittelpunkt des Kuboktaeders
mit seinen Eckpunkten, kann man Vertiefungen in Form von geraden Pyramiden
erkennen. Je nach Sichtweise sind das dreiseitíge oder quadratische
Pyramiden.
...
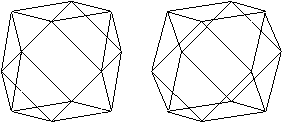
...Kuboktaeder |
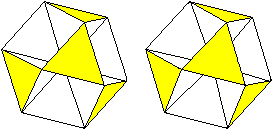
Oktahemioktaeder |
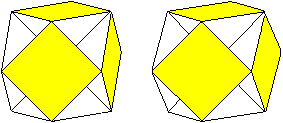
Kubohemioktaeder |
Nach diesem Prinzip gelangt man von vielen
Deltaedern zu neuen Deltaedern, indem man Vertiefungen in Form von Tetraedern
erzeugt.
Deltaeder im weiteren Sinne
Das abgestumpfte Tetraeder
ist ein Körper, der von 4 regelmäßigen Sechsecken und 4
gleichseitigen Dreiecken gebildet wird.
Da sich das Sechseck in sechs gleichseitige Dreiecke
zerlegen lässt, wird er aus 4*6+4 = 28 Dreiecken gebildet. Man könnte
ihn deshalb auch als Deltaeder im weiteren Sinne bezeichnen.
... |
 |
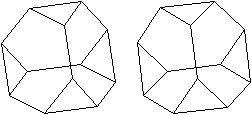Das abgestumpfte Tetraeder steht für viele Körper
dieser Art.
Geodätische Kuppel
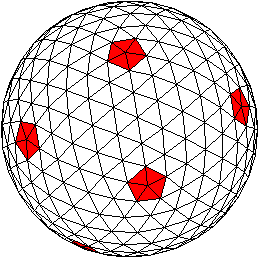Mehr auf Werner Brefelds Seite (URL unten)
Bau von Deltaedern
top
Will man sich mit Deltaedern beschäftigen, empfiehlt
es sich, sie selbst zu bauen.
... ... |
Da bieten sich Modelle aus Papier an, geklebt mit Hilfe
der Netze.
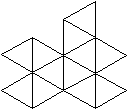
Die nebenstehende Vorlage z.B. zum Ikosaeder - größer
- findet man auf meiner Seite Platonische Körper. |
... ... |
Es gibt die Möglichkeit, z.B. den Körper J
51 sehr einfach aus Zahnstochern als Kanten und Kügelchen aus Knete
als Ecken zu bauen. |
... ... |
Es gibt auch die Möglichkeit, den gleichen Körper
aus Stabmagneten als Kanten und Eisenkugeln als Ecken zu bauen. |
Deltaeder im Internet
top
Deutsch
Christoph Pöppe (spektrumdirekt)
Folge
6: Körper aus lauter Dreiecken
Udo Hebisch (Mathematisches Café)
Die
Familie der (konvexen) Deltaeder
Werner Brefeld
Geodätische
Kuppeln
Wikipedia
Deltaeder,
Geodätische
Kuppel, Sterntetraeder
Englisch
Eric W. Weisstein (MathWorld)
Deltahedron,
Boat
George W. Hart
Convex
Deltahedra, Johnson
Solids
mathworld.wolfram
Spikey
Maurice Starck
the
eight convex deltahedra
Poly-pro 1.09
A program for downloading
(Poly is a shareware program for exploring and constructing polyhedra)
Die meisten Bilder auf dieser Webseite wurden mit
diesem Programm erstellt.
Tom Gettys
Deltahedra
Wikipedia
Deltahedron,
Geodesic
dome, Stellated
octahedron
Referenzen top
(1) F.L. Bauer, Einladung zur Mathematik,
Deutsches Museum, München (ISBN 3-924-18349-X)
(2) M.Odier, Y.Roussel: Troiker
mathematisch gespielt, Braunschweig, Wiesbaden 1979 (ISBN 3-5 28-08394-8)
(Seite 79 ff.)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003, überarbeitet 2015, Jürgen Köller
top |
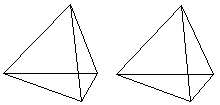
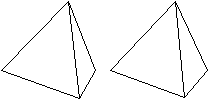
