|
Was ist das Hypertetraeder?
Das Hypertetraeder ist das vierdimensionale Tetraeder.
Schrägbild top
Das vierdimensionale Tetraeder ist ein Gedankengebilde.
Man kann sich ihm durch Analogieüberlegungen nähern, man geht
vom Tetraeder zum Hypertetraeder. Legitimiert wird das Vorgehen durch das
Permanenzprinzip, das in der Mathematik häufig angewandt wird, um
"vom Bekannten zum Unbekannten" zu gelangen.
. .. |
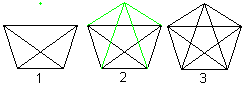Verbindet man die Eckpunkte eines Tetraeders (1) mit
einem fünften Punkt (2), so entsteht das Schrägbild eines Hypertetraeders
(3). |
Während ein Viereck mit den beiden Diagonalen das Schrägbild
eines Tetraeders ist, stellt ein Fünfeck mit den Diagonalen das Bild
des Hypertetraeders dar.
Eigenschaften top
Das Hypertetraeder hat 5 Ecken (1 Tetraeder und der fünfte
Punkt) und 10 Kanten (1 Tetraeder mit 6 Kanten und 4 Verbindungslinien
zum fünften Punkt).
Das Hypertetraeder hat 10 Dreiecke.
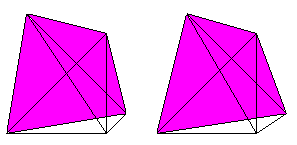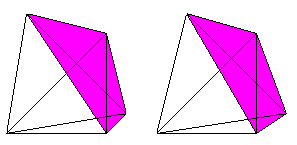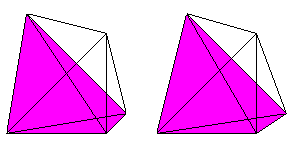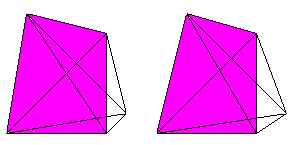
So wie das Tetraeder von vier Dreiecken wird das Hypertetraeder
von fünf Tetraedern gebildet.
Wer den 3-D-Blick beherrscht, sieht die fünf Tetraeder
in etwas anderer Ansicht auch räumlich.
An jeder Ecke des Hypertetraeders stoßen 4 Tetraeder,
6 Dreiecke und 4 Kanten zusammen.
An jeder Kante des Hypertetraeders stoßen 3 Tetraeder
und 3 Dreiecke zusammen.
An jeder Fläche des Hypertetraeders stoßen
2 Tetraeder zusammen.
Projektionen
top
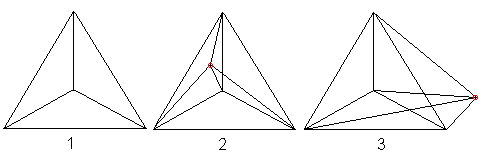Wenn man die Aufsicht eines Tetraeders (Zentralprojektion)
(1) vorgibt und einen fünften Punkt (rot) innerhalb (2) oder außerhalb
(3) wählt, erhält man zwei Darstellungen des Hypertetraeders.
Das Hypertetraeder 2 ist ein Dreieck mit gewissen Linien
im Inneren, das Hypertetraeder 3 ein Viereck, während oben der Umriss
ein Fünfeck ist.
Man erkennt in den Figuren 2 und 3, dass an jeder Ecke
vier Kanten zusammentreffen.
Netze top
.. .... |
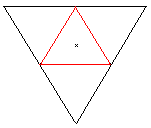Klappt man das Tetraeder auf, so entsteht sein Netz.
Die 4 Dreiecke haben zusammen 4*3=12 Seiten. 2*3=6 Seiten (rot) sind gebunden.
Beim Zusammenbau des Tetraeders müssen die restlichen 6 Seiten paarweise
zusammengeklebt werden.
Es gibt 2 verschiedene Netze. |
 ... |
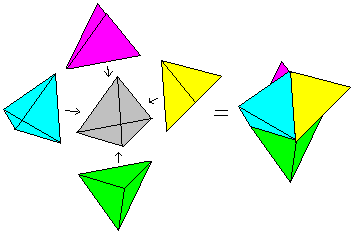Klappt man das Hypertetraeder auf, so entsteht als Netz
ein Körper aus 5 Tetraedern. Die fünf Tetraeder haben zusammen
5*4=20 Dreiecke. 2*4=8 Dreiecke sind gebunden. Beim Zusammenbau des Hypertetraeders
müssen die restlichen 12 Dreiecke paarweise zusammengeklebt werden. |
Formeln top
Die obigen Überlegungen erhalten durch Formeln eine
sicherere Grundlage.
"Tetraeder" mit den Dimensionen 1, 2 und 3 haben folgende
Eigenschaften.
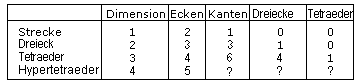Man müsste in der nächsten Zeile die Daten des
Hypertetraeders bestimmen. Dimension=4, Ecken=5 ist klar. Wie die Folge
der Kanten und Dreiecke fortgesetzt werden muss, beschreibt das folgende
Bildungsgesetz.
Setzt man in die Terme der Tabelle n=4, so erhält
man für das Hypertetraeder folgende Daten.
Für das 5-dimensionale Tetraeder ergibt sich:
Hypertetraeder
im Internet top
Deutsch
Marco Möller
Polytope
Wikipedia
Pentachoron
Englisch
Eric W. Weisstein, (MathWorld)
Regular
Polychoron, Pentatope,
Simplex
Paul Bourke
HyperSpace,
User Manual
NN
Pentatope
Wikipedia
Pentatope
Referenzen top
(1) Fritz Reinhardt, Heinrich Soeder: dtv-Atlas zur Mathematik
I (Seite 172), München 1977
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |