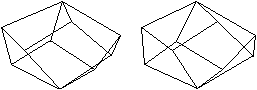|
Was ist ein quadratisches Antiprisma?
... ... |
Das quadratische Antiprisma ist ein Körper,
der von zwei Quadraten und acht gleichseitigen Dreiecken gebildet wird.
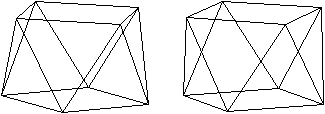
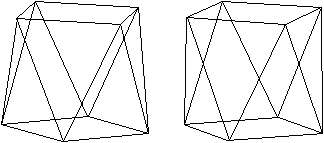
3D-Ansicht
|
Beschreibung
top
... ... |
 ... |
Zwei kongruente Quadrate liegen parallel und sind gegeneinander um
45° um eine Achse durch ihre Mittelpunkte gedreht.
Die Eckpunkte der Quadrate werden durch eine Zickzacklinie miteinander
verbunden, so dass acht kongruente, gleichseitige Dreiecke entstehen. |
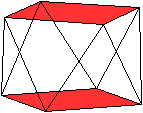
Die beiden Quadrate bilden die Grundflächen des Körpers, die
Dreiecke den Mantel.
Der Körper hat neben den 10 Flächen
8 Eckpunkte und 16 Kanten.
| Liegen die beiden Quadrate parallel zur Zeichenebene, so ergeben sich
folgende Ansichten. |
... ... |
 |
|
 |
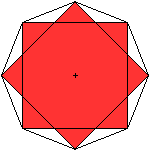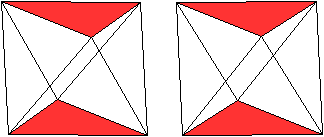
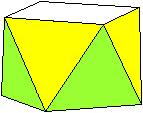
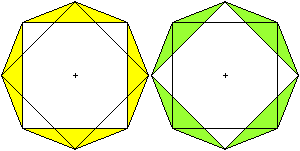
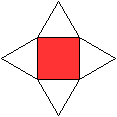
Jedes Quadrat ist von vier Dreiecken umgeben.
Jedes Dreieck ist von einem Quadrat und zwei Dreiecken umgeben. |
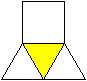
In jedem Eckpunkt treffen ein Quadrat und
drei Dreiecke aufeinander.
Die Gerade durch die Mittelpunkte der Quadrate
ist eine Symmetrieachse mit vierstrahliger Drehsymmetrie.
Besondere Ansichten
top
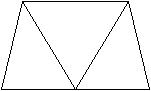
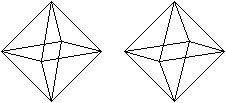
Die Quadrate erscheinen als Strecken.
|
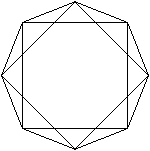
durchsichtig
|
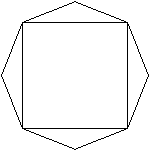
undurchsichtig
|
Die Quadrate liegen parallel zur Zeichenebene.
|
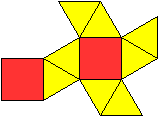
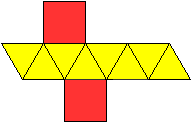
Netze
top
Größen
top
|
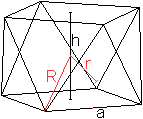Ein quadratisches Antiprisma ist i.a. durch die Kantenlänge a
gegeben.
Der Abstand der Quadrate und gleichzeitig die Höhe ist h.
Es gibt eine Umkugel mit dem Radius R, deren Mittelpunkt M auf
halber Höhe liegt.
Der Abstand des Mittelpunktes eines Dreiecks vom Mittelpunkt des Körpers
ist r.
Die Oberfläche ist O und das Volumen V. |
Formeln
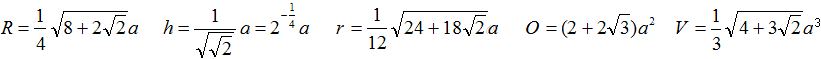
Zu den Herleitungen
Höhe h
... ... |
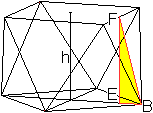Man findet im Körper das rechtwinkliges Dreieck BEF.
Es gilt EF=h, EB=(1/2)sqrt(2)a-(1/2)a und FB=(1/2)sqrt(3)a als Höhe
im gleichseitigen Dreieck.
Nach dem Satz des Pythagoras ist FB²=EB²+EF² oder h²
=(3/4)a²-(1/4)([sqrt(2)-1]²a² =(3/4)a²-(1/4)[2-2sqrt(2)+1]a²
=(1/2)sqrt(2)a².
Dann ist h =sqrt[(1/2)sqrt(2)]a =1/sqrt[sqrt(2)]a=2-1/4a. |
Radius der Umkugel R
... ... |
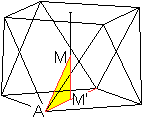Im rechtwinkligen Dreieck AM'M ist AM der gesuchte Radius R.
Es gilt R² =AM'²+M'M² =[(1/2)sqrt(2)a]²+(h/2)²
=a²/2+(1/4)(1/2)sqrt(2)a² =a²/2+(1/8)sqrt(2)a²
=8a²/16+[2sqrt(2)]/16 =(1/16)[8+2sqrt(2)]a².
Dann ist R=(1/4)sqrt[8+2sqrt(2)]a |
Abstand r
... ... |
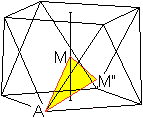Im rechtwinkligen Dreieck MAM'' ist r=MM''.
Es gilt r² =AM²-AM''² =R²-[(2/3)(1/2)sqrt(3)a]²
=a²/2+(1/8)sqrt(2)a²-a²/3 =a²/6+(1/8)sqrt(2)
=(24/144)a²+18sqrt(2)a²/144 = (1/144)[24+18sqrt(2)]a²
Dann ist r=(1/12)sqrt[24+18sqrt(2)]a |
Oberfläche O
O=2*a²+8*[(1/4)sqrt(3)a²]= [2+2sqrt(3)]a²
Volumen V
Im Mittelpunkt M treffen sich die Spitzen von zwei quadratischen Pyramiden
und acht dreiseitigen Pyramiden.
Das Gesamtvolumen ist
V=2*(1/3)a²(h/2)+8*(1/3)[(1/4)sqrt(3)a²]r =(1/3)(2-1/4)a³+(2/3)sqrt(3)a²*(1/12)sqrt[24+18sqrt(2)]a
={(1/3)(2-1/4)+(1/6)sqrt[8+6sqrt(2)]}a³.
Die Formel scheint falsch zu sein, denn in der Literatur findet man
die einfachere Formel V=(1/3)sqrt[4+3sqrt(2)]a².
Das ist nicht der Fall. Es gilt die Identität {(1/3)(2-1/4)+(1/6)sqrt[8+6sqrt(2)]}
= (1/3)sqrt[4+3sqrt(2)].
Das kann man durch zweimaliges Quadrieren nachweisen.
Ein Vergleich
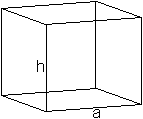
Betrachtet man das Antiprisma oberflächlich, so hat es etwa die
Form eines quadratischen Prismas
mit der Höhe h und der Grundseite a.
|
......
|
 ...
|
Es gilt für beide Körper h=0,84a
Prisma
R=0,82a
r=0,5a
V=0,84a³
O=5,36a²
|
Antiprisma
R=0,84a
r=0,59a
V=0,96a³
O=5,46a²
|
|
Die Zahlen sind auf zwei Dezimalen gerundet.
Weitere Antiprismen
top
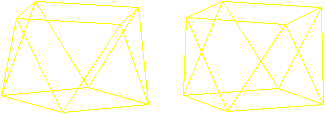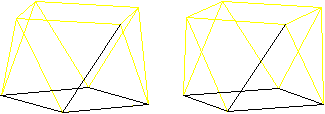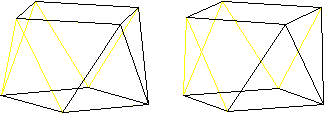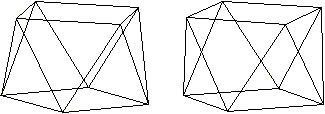
Allgemeines quadratisches Prisma
Verändert man den Abstand der Quadrate des oben vorgestellten
Antiprismas, so werden die gleichseitigen Dreiecke zu gleichschenkligen.
Der Name quadratisches Antiprisma trifft weiter zu.
Man nennt das linke Prisma mit den gleichseitigen Dreiecken genauer
regelmäßiges
quadratisches Antiprisma.
Antiprismen aus Vielecken
Ersetzt man die Quadrate durch regelmäßige n-Ecke, so erhält
man weitere Antiprismen. Die beiden parallel liegenden regelmäßigen
Vielecke sind um 180°/n gegeneinander verdreht. Der Mantel wird aus
2n gleichseitigen Dreiecken gebildet.
.
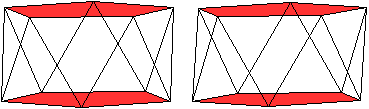
Pentagonales Antiprisma
|
Dekagonales Antiprisma
|
Auch das Oktaeder ist ein Antiprisma mit
gleichseitigen Dreiecken als Grundseiten.
Noch einmal V
Man kann Formeln für das quadratische Antiprisma auch so herleiten,
dass man Formeln für ein Antiprisma mit einem regelmäßigen
n-Eck als Grundseiten herleitet und dann auf n=4 spezialisiert.
Es gilt z.B.
 .
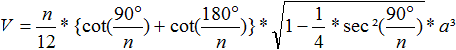Man findet eine Herleitung bei Literka (URL unten). Der Weg entspricht
dem der Herleitung oben.
Die Formel wird einfacher, wenn man das
Volumen durch die Höhe h ausdrückt.
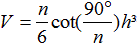Man findet die Formel auf der französischen Wikipedia-Seite und eine
Herleitung bei numericana (URL unten).
Abgeschrägtes
quadratisches Antiprisma
Bei diesem Körper liegt zwischen zwei quadratischen
Grundflächen ein Geflecht aus 24 gleichseitigen Dreiecken.
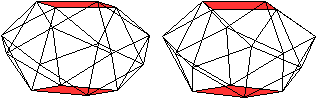
3D-Ansicht
|
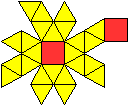
Netz
|
Der Körper hat neben den 26 Flächen 16 Eckpunkte und 40 Kanten.
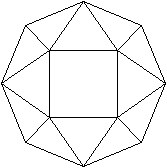
Besondere Ansichten
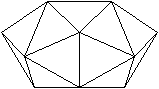
Die Quadrate erscheinen als Strecken.
|
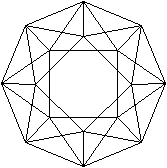
durchsichtig
|
undurchsichtig
|
Die Quadrate liegen parallel zur Zeichenebene.
|
Dieser Körper wird nur von regelmäßigen Vielecken begrenzt
und ist ein Johnson-Körper, und zwar Johnson-Körper J85.
Dualer Körper
top
Verbindet man die Flächenmitten der Seitenflächen des quadratischen
Prismas miteinander, so entsteht der duale Körper.
Er heißt quadratisches Deltohedron
oder quadratisches Trapezoeder.
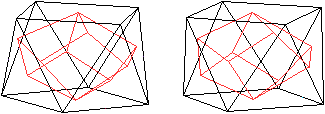
Eulerkreis
top
Mehr auf der Seite Haus des Nikolaus
Quadratisches
Antiprisma im Internet top
Deutsch
Hans-Bernhard Meyer
Quadratisches
Antiprisma (Polyeder aus Flechtstreifen)
Wikipedia
Prisma (Geometrie)
Englisch
Hans-Bernhard Meyer
Square
Antiprism (Polyhedra plaited with paper strips)
Eric W. Weisstein (MathWorld)
Square
Antiprism, Antiprism,
Trapezohedron,
Tetragonal
Trapezohedron
George W. Hart
Prisms
and Antiprisms
Honeylocust Media Systems
Square
Antiprism
Literka
Antiprisms.
Volume Formula
numericana
What
is the volume of a regular antiprism?
Poly
A program for downloading
(Poly is a shareware program for exploring and constructing polyhedra)
Die Zeichnungen auf dieser Seite entstanden mit Hilfe dieses Programms.
Wikipedia
Square antiprism,
Antiprism,
Trapezohedron,
Compound
of three square antiprisms, Apeirogonal
antiprism
Französisch
Robert FERRÉOL (mathcurve)
ANTIPRISME
Wikipedia
Antiprisme
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |
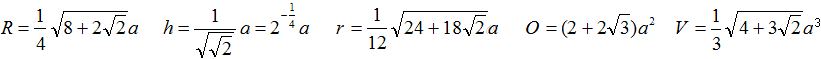
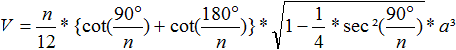