|
What is the Bascetta-Star?
... ... ... |
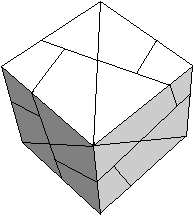
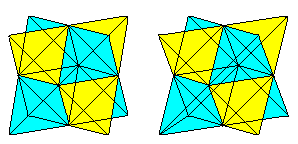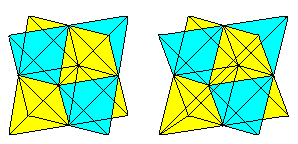
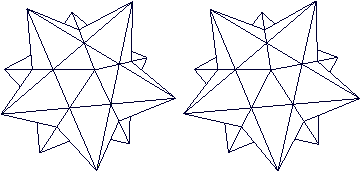
The Bascetta Star is a three-dimensional star that is
assembled from 30 modules.
The modules are folded from squares.
Mathematically, it is an icosahedron with 20 triangular
pyramids on its sides. |
The name goes back to the inventor of the module and the
star, the Italian Paolo Bascetta.
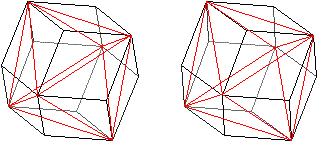
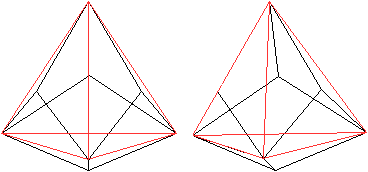
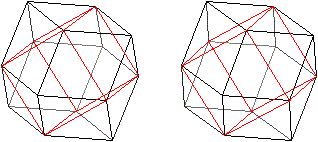
Comparison
with the Great Stellated Dodecahedron top
The great
stellated dodecahedron has the same structure. It is also an icosahedron
with straight triangular pyramids as the crown, but the pyramids are more
pointed.
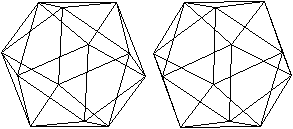
Ikosaeder
|
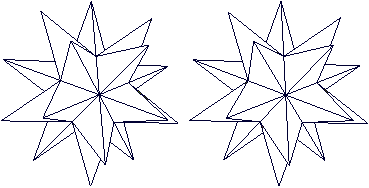
|
...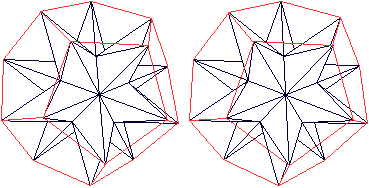 ... ... |
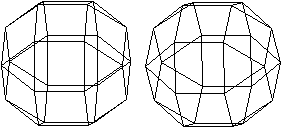
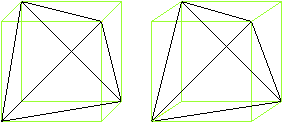
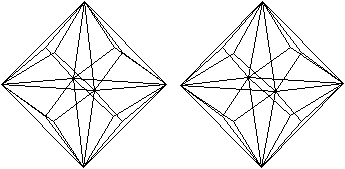
The name dodecahedron is explained by the fact that a
dodecahedron is formed, when you connect the vertices.
The image pairs become three-dimensional with the 3D view. |
... ... ... |
The Bascetta star is related to the Sonobe
star, which is also a stellated icosahedron and which is also assembled
from 30 modules. |
Folding
a Module top
... ... ... |
You need 30 squares of paper for the star.
You can use the 9cm x 9cm note paper. |
11
steps
01
...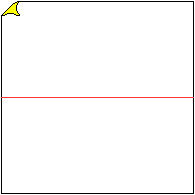 ... ... |
Halve the square with a valley fold.
It is convenient that for this fold and the following
ones you do not just go over the crease with your finger, but, for example,
with a pair of scissors inverted.
 |
02
...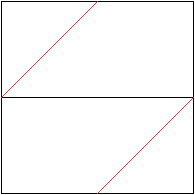 ... ... |
Fold on the red lines.
 |
03
...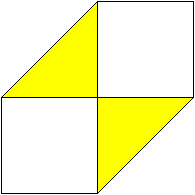 ... ... |
It should look like this.
 |
04
...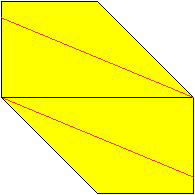 ... ... |
Turn the paper over and fold along the red lines.
 |
05
...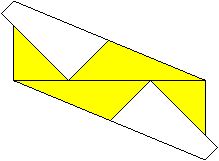 |
It should look like this.
 |
06
...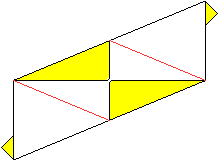 ... ... |
Turn the paper over and fold along the red lines.
 |
07
...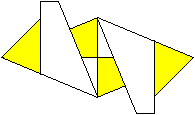 ... ... |
It should look like this.
 |
08
...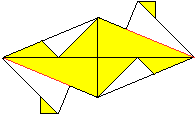 ... ... |
Turn the paper over and fold along the red lines.
 |
09
...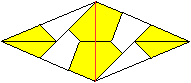 ... ... |
It should look like this.
Fold along the red lines.
 |
10
...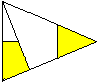 ..................... ..................... |
It should look like this.
 |
11
...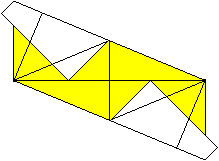 ... ... |
Unfold the triangle several times until you get back
to figure 05. |
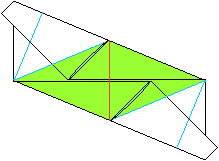
... ... ... |
You have to go through it.
Fold the module 29 more times. |
... ... ... |
It should be noted that each module contributes to two
faces of adjacent pyramids. |
Joining to
Form a Pyramid top
...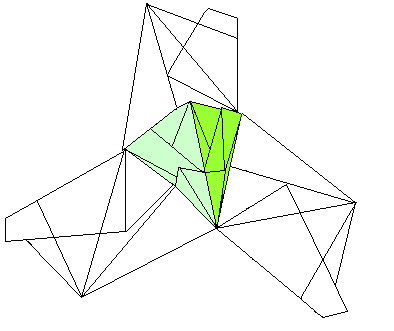 . . |
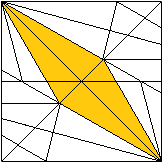
Three modules are plugged together to form a pyramid. |
And it goes like this.
...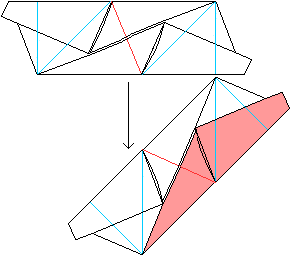 ... ... |
Put one module into the (pink) pocket of a second module. |
...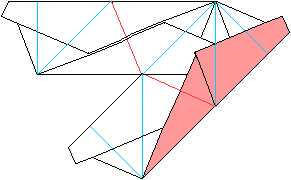 ... ... |
It should look like this. |
...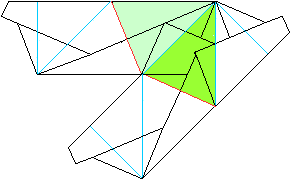 ... ... |
This is already two side faces of a pyramid.
The upper face is folded backwards. |
 |
A third module encloses the first two and is fixed.
The first pyramid is finished. |
Assembling the Star
top
Modules, each forming another pyramid,
are added to the first pyramid one after the other until the star finally
closes.
... ... ... |
It is a great help in the resulting confusion if you
imagine the generating icosahedron:
Five triangles meet at each vertex.
This means that five pyramids always form a wreath. |
Some Mathematics
top
...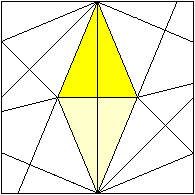 ... ... |
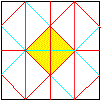
If you unfold the module, you will recognise two side
faces of pyramids as isosceles triangles.
The angle at the top of one triangle is 22.5° because
of the folding process.
The height of the triangle is half the side length of
the square. |
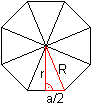
The angle 22.5° also
occurs in the basic triangle of the regular octagon.
... ... ...
|
Therefore, the following formulas can be adopted.
If the base a is given, then the height in the
triangle is r = (1/2)[sqrt(2)+1]a (rounded r = 1.207a)
and the leg is R = (1/2)sqrt[4+2sqrt(2)]a (rounded R
= 1.307a). |
Three questions
will be answered.
Question 1
Only a small part of the square
area A of the module is used. What percentage is this?
The
two isosceles triangles together have the area 2A = ar.
The square of the module has the
area A = 4r².
Then (2A)/A = (ar)/(4r²) =
a/(4r) = 1/[2(sqrt(2)+1)] = (1/2)[sqrt(2)-1] = 0.207 = 20.7%.
Result
About 20% of the area of the initial
square is used.
Question
2
What is the height H of a pyramid?
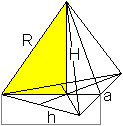 |
According to the Pythagorean theorem
H² = (1/4)[4+2sqrt(2)]a²-[(2/3)(1/2)sqrt(3)]²a²
= [1+(1/2)sqrt(2)-1/3]a² = [2/3+(1/2)sqrt(2)]a²
= (1/36)[24+18sqrt(2)]a²
Then H = (1/6)sqrt[24+18sqrt(2)]a (rounded H = 1,172a) |
Result
The height of a pyramid is H = (1/6)sqrt[24+18sqrt(2)]a
(rounded 1.172a).
According to the website
of wikipedia, the height of the pyramid of the Great Stellated Dodecahedron
is
k = (1/6)[3sqrt(3)+sqrt(15)] = 1.516a, so it is larger
than the pyramid of the Bascetta star.
Question
3
How big is the star?
This refers to the distance e between the tips of two
opposite pyramids.
> The distance between opposite
sides of the icosahedron is d=(1/6)[3sqrt(3)+sqrt(15)]a =1.152a.
> The height of a pyramid is H = (1/6)sqrt[24+18sqrt(2)]a
= 1.172a.
Then e = 2H+d = (1/3)sqrt[24+18sqrt(2)]a+(1/6)[3sqrt(3)+sqrt(15)]a
(rounded e = 3.496a).
It is convenient to relate the distance e to the side
length 2r of the initial square.
It is r = 1.207a or a = 0.829r. Then e = 3.496a = 3.496*0.829r
= 2.898r = 1.450(2r).
With 2r = 9cm, e = 13.04cm.
Results
If the side length of the initial square is 9cm, the
star will be 13.04cm.
The ratio e/(2r) is 1.45. The star is about 50% bigger
than the side length of the square.
More Figures
from the Modules top
Rudolf Kunstmann, who suggested this website, has obviously
worked intensively with solids from the Bascetta modules and their variants.
With his permission I show a small selection of his stars.
Stellated
octahedron
Star
to the cubeoctrahedron
Star to the rhombicuboctahedron
Star
to the snub cube
Figure from
other Modules top
On my website Körper flechten
I use another module to build a cube.
Modular origami is a broad field on which you can find a
lot in literature and on the internet.
Stellated Polyhedra
top
Stellated polyhedra are convex polyhedra with straight
pyramids on their sides.
Here are a list of solids of this type that can be found
on my homepage (German only).
Bekröntes
Tetraeder
Hypertetraeder
Bekröntes Oktaeder
 ... ...
Rhombendodekaeder
Bekrönter
Würfel
Bekröntes
Ikosaeder und bekröntes Pentagondodekaeder
Bekröntes
Rhombendodekaeder
Bekröntes
Kleines Rhombenkuboktaeder
... ..... ..... |
If you crowns the rhombicuboctahedron,
the result is a star made of 18 square pyramids
and eight triangular ones.
This is the shape of the well-known Herrnhut Stern or
Moravian Star. |
... |
This is the Herrnhut Star, built from a kit (12/2013). |
There is now (05/2022) another
web page on a stellated icosahedron made of 20 squares, the Kusudama
star.
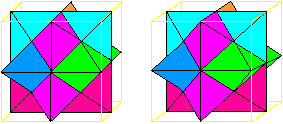
Comparison
of three stars
|
a=9,0cm
|
Sonobe Star
|
Bascetta Star
|
Kusudama Star
|
|
2A/Aq
|
12,7%
|
20,0%
|
26,8%
|
|
H
|
0,29a = 2,6cm
|
0,49a = 4,4cm
|
0,70a = 6,3cm
|
|
e
|
1,04a = 9,4 cm
|
1,45a = 13,1cm
|
1,97a = 17,7cm
|
|
Sonobe Star
|
Bascetta Star
|
Kusudama Star
|
|

|
|
Bascetta
Star on the Internet top
Deutsch
Annerose Gemeinhardt
Bascetta
Stern (.pdf-Datei)
Paolo
Bascetta ist bei Facebook.
Stephanie Meschke
3d-Stern,
Sonobe-Stern
(.pdf Dateien)
Wikipedia
Bascetta-Stern,
Sternkörper,
Herrnhuter
Stern,
Weihnachtsstern
(Symbol)
Englisch
Jo Nakashima
Origami
Bascetta Star (Video)
Origami-Resource-Center.com
Sonobe
Stellated Octahedron (12 units)
Wikipedia
Sonobe,
Moravian
star,
Star polyhedron,
Polyhedral
compound, Modular
origami, Mitsonobu
Sonobe
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2021 Jürgen Köller
top |

 ...
...
 ...
...

 ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... .....................
..................... ...
... ...
... ...
... .
. ...
... ...
... ...
... ...
... ...
...












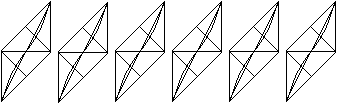


 .....
.....

