|
What ist the Kusudama Star?
... ...
This is the first of 20 pyramids ...
This is the first of 20 pyramids
|
On the internet I found under the
name Kusudama Star a series of stars which, like the Bascetta and Sonobe
stars, are folded of 30 modules and which are also stellated icosahedra.
For this page I have chosen the
"Origami Igel Kusudama", whose construction is shown in a Youtube video
(belongs to "Katrin Origami Page"). The inventor of the module and the
star is Ekaterina Lukasheva. |
I have chosen the star because the
pyramids are more pointed and thus more handsome than the pyramids of the
Bascetta star. - It is remarkable, that the module uses the creation of
a 30° angle by folding alone (step 4 below).
There
are own pages for the Sonobe Star and the Bascetta Star.
Folding
the Kusudama Module top
Materials
... ... ... |
You need 30 squares of paper for the star.
The 9cm x 9cm notepads that you can buy in stationery
shops would be a good choice.
They were good for the Bascetta and the Sonobe Star. But
for this star they are unsuitable in my opinion. You have to use thin origami
paper like shown in the video. I did that and it worked better. |
12
Steps
1
2
...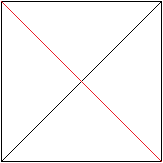 ......... ......... |
Fold on the red line and unfold again.

 |
3
...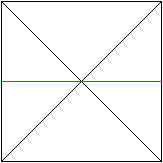 ... ... |
Fold on the red line and unfold again.
 |
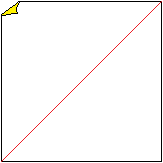
4
...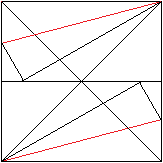 ... ... |
Fold on the red lines so that the corners of the square
touch the centre line.
 |
5
...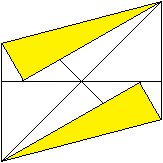 ... ... |
This should look like the picture
on the left.

 |
6
..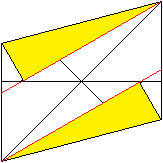 .... .... |
Fold on the red lines. The lower line and the upper line
should meet the diagonal.
 |
7
...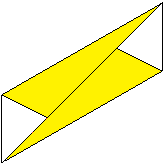 |
It should then look like this.

 |
8
...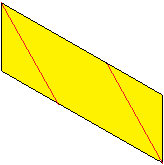 |
Turn over the module and fold on the red lines. Unfold
again.

 |
9
...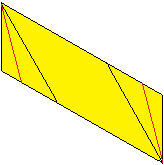 |
Fold on the red line.

 |
10
...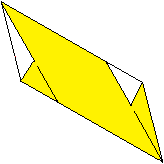 . . |
It should then look like this. Unfold.


 |
11
...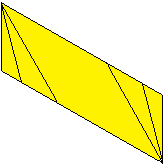 |
It should then look like this.

 |
12
Assembling the Star
top
...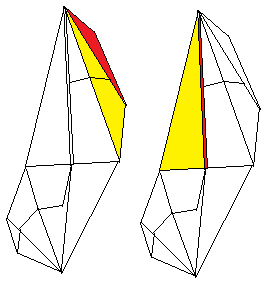 |
Connect two modules.
To do this, put the red flap into the red pocket. Then
the yellow triangles lie on top of each other.


 |
... ... ... |
It should look like this.
The flap did not stick in the pocket; a paper clip helps.

 |
... ....... ....... |
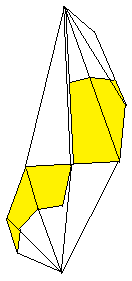
Enclose the two connected modules with a third module.
The first pyramid is finished.
Then add more modules step by step and form more pyramids.
When doing this make sure that five pyramids always form a wreath.


|
... ... ... |
At this point, the finished Kusudama star with 20 pyramids
should actually be stand.
For various reasons, I offer a smaller star made of 12
modules with eight pyramids.
The star is a stellated octahedron in which a wreath always
consist of four pyramids. |
My Experiences
with Notes top
... ... ... |
... ... ... |
If the modules are folded from notepads, the result is
unsatisfactory.
- As you can see on the left, the tip of the pyramid
is frayed. It is hardly possible to make five folding lines at one corner
of the notepads. The paper also often tears.
- Then the pockets are so open and the flaps so
small that I need paper clips to hold the modules together. |
Some Mathematics top
...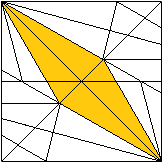 ... ... |
If you unfold the module, you will recognise the side
faces of two pyramids as isosceles triangles.
The angle at the top of a triangle is 30° because
of the folding process, the height of a triangle is half the diagonal of
the square with the side a. |
Maybe
three questions are interesting.
1st Question
Only a small part of the square
area Aq of the module is used. What percentage is this?
Answer
...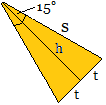 ... ... |
Ahead: tan(15°) = 2-sqrt(3)
In the half isosceles triangle the height h=(1/2)sqrt(2)*a
and the angle of 15° are known.
tan(15°) = t/h then t = h/tan(15°) = [sqrt(2)-(1/2)sqrt(6)]a
= 2*[2sqrt(2)-sqrt(6)]a .
The area of the side face of a pyramid is A = (1/2)(2t)h
= th = (1/2)[2-sqrt(3)]a² or rounded 0,134a². |
Two isosceles triangles contribute
to the formation of the star. They have the area 2A,
The square of the module has the
area Aq = a², then rounded 2A/Aq = 0,268.
Result
About 27% of the area of the initial
square is used.
2nd
Question
What is the height H of a pyramid?
Antwort
... ... ... |
Ahead: cos(15) = (1/4)[sqrt(2)+sqrt(6)]
s = h/cos(15°) =[2sqrt(2)/(sqrt(2)+sqrt(6))]a = [sqrt(3)-1]a.
The height in the equilateral triangle with side 2t is
h' = (1/2)sqrt(3)(2t). |
...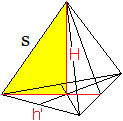 ... ... |
According to the theorem of Pythagoras the following
applies
H² = s²-[(2/3)h']² = [sqrt(3)-1]²a²-[(2/3)(1/2)sqrt(3)2t]a²
= [sqrt(3)-1]²a²-[(2/3)sqrt(3)t]a²
=[sqrt(3)-1]²a²-[(2/3)sqrt(3)(sqrt(2)-(1/2)sqrt(6))]²a²
= [sqrt(3)-1]²a²-[2/3sqrt(6)-sqrt(2)]²a²
= [4-2sqrt(3)]²a²-[14/3-8/3sqrt(3)]a²
= [-2/3+2/3sqrt(3)]a².
Then H = (1/3)sqrt[6sqrt(3)-6]a. |
Result
The height of a pyramid is H = (1/3)sqrt[6sqrt(3)-6]a
or rounded H = 0.699a.
If the side length of the initial square is a = 9 cm,
the height is H = 6.3 cm.
3rd
Question
How big is the star?
This means the distance e of the tops of two opposite
pyramids.
Answer
The distance between opposite side faces of the icosahedron
is twice the radius of the incircle.
d = (1/6)[3sqrt(3)+sqrt(15)](2t) = (1/6)[3sqrt(3)+sqrt(15)][2sqrt(2)-sqrt(6)]a
or rounded d=0.571a.
The distance is e = 2H+d = 2*0.699a+0.573a = 1.971a.
Result
If the side length of the initial square is a = 9.0 cm,
the size of the star will be 17.7 cm.
Comparison of three stars
|
a=9,0cm
|
Sonobe Star
|
Bascetta Star
|
Kusudama Star
|
|
2A/Aq
|
12,7%
|
20,0%
|
26,8%
|
|
H
|
0,29a = 2,6cm
|
0,49a = 4,4cm
|
0,70a = 6,3cm
|
|
e
|
1,04a = 9,4 cm
|
1,45a = 13,1cm
|
1,97a = 17,7cm
|
|
Sonobe Star
|
Bascetta Star
|
Kusudama Star
|
|
|

|
Kusudama
Stars on the Internet top
Ten Links to Stars with 20 Pyramids
1.Stern: Sonobe-Star
2.Stern: Bascetta-Star
3. Stern: Origami
Igel Kusudama (Youtube)
Und weiter
4. Stern: Origami
Radianta Kusudama (Youtube)
5. Stern: Origami
Modular Star (Bascetta-Stern, gespiegelt)
6. Stern: How
to fold an Origami Modular Star (Youtube)
7. Stern: 30-unit
Sky Star Kusudama (Creator: Maria Sinayskaya) (Youtube)
8. Stern: Origami
Kusudama/ 3D Star Ball for Christmas/ Paper 30-point Star (Youtube)
9. Stern: Origami
Estramallar Origami (Youtube)
10. Stern: Tutorial
for Origami Sonobe Variation Kusudama 30 (Youtube)
More Links
Elisa (japanliebe.de)
kusudama
– was haben origami-Bälle mit Medizin zu tun?
Katrin
Origami
die Kunst des Papierfaltens
Wikipedia
Kusudama
Youtube
PopUp
Star
Youtube
Kusudama
estrella Ostrum
Youtube
Dreiecke
durchdringen sich
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
May 2022 Jürgen Köller
top |
 ...
...
 .
.

 ...
... ....
.... .........
......... ...
... ...
... ...
... ....
....


 .
.

 ...
... ...
... ...
... ...
... ...
... ...
... ...
...
