|
Kleines Rhombenkuboktaeder
|
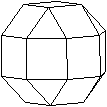
Was ist das kleine Rhombenkuboktaeder?
... ...
|
Das kleine Rhombenkuboktaeder (kurz:
Rhombenkuboktaeder) ist ein Körper, der von 18 Quadraten und
8 gleichseitigen Dreiecken gebildet wird.
Neben den 18+8=26 Seitenflächen hat es 48 Kanten
und 24 Eckpunkte. |
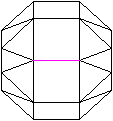
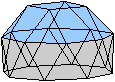
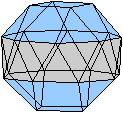
Die beiden folgenden, nebeneinander
liegenden Bilder ermöglichen mit dem "Stereoblick" eine dreidimensionale
Ansicht.
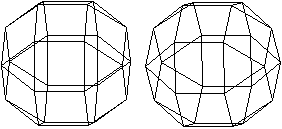
durchsichtig
|
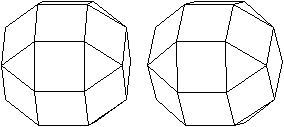
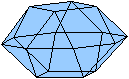
undurchsichtig
|
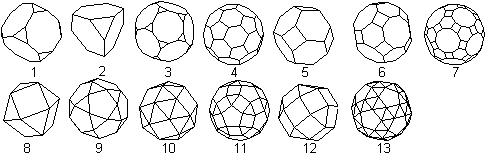Da beim Rhombenkuboktaeder (12)
an jeder Ecke regelmäßige Vielecke in gleicher Weise aufeinandertreffen,
gehört er zu den 13
archimedischen Körpern.
Beschreibung top
Umgebung der Dreiecke und Quadrate
... |
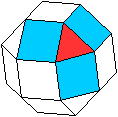Jedes Dreieck ist von drei Quadraten umgeben. |
... |
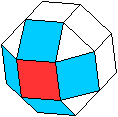Entweder:
Ein Quadrat ist von vier Quadraten umgeben. |
... |
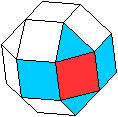Oder:
Ein Quadrat ist von von zwei Dreiecken und zwei Quadraten
umgeben. |
Parallelprojektionen
Ein Quadrat, ein Dreieck, eine
Kante 3/4, eine Kante 4/4 und ein Eckpunkt liegen vorne.
Netz
|
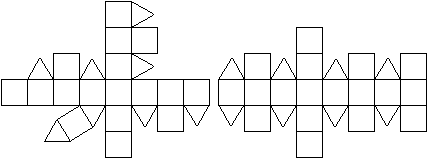
Zwei Netze des Rhombenkuboktaeders |
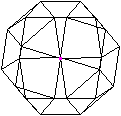
Schlegel-Diagramm
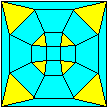
Diagonalen
36 Flächendiagonalen
... .... |
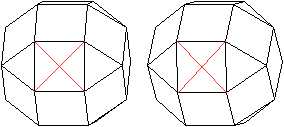Die Diagonalen der Quadrate sind die Flächendiagonalen
des Rhombenkuboktaeders.
Das Quadrat hat 2 Diagonalen.
Das führt zu insgesamt 18*2=36 Flächendiagonalen. |
192
Raumdiagonalen
... ... |
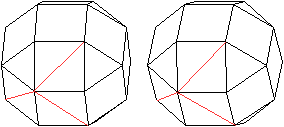Von jedem der 24 Eckpunkte gehen Verbindungslinien zu
den anderen Eckpunkten aus. Das sind 3 Flächendiagonalen und 4 Kanten,
wie die Zeichnung zeigt. In 24-7=17 Punkten enden dann Raumdiagonalen.
Das führt zu insgesamt (1/2)*24*16=192 Raumdiagonalen des Rhombenkuboktaeders. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das Rhombenkuboktaeder
bedeutet das, dass es (1/2)*23*24=276 Verbindungslinien gibt.
Das sind die 48 Kanten, 36 Flächendiagonalen und
192 Raumdiagonalen.
Entstehung top
Vom Würfel zum kleinen Rhombenkuboktaeder
... ... |
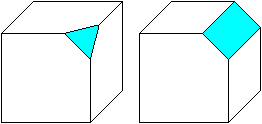Eine Reihe archimedischer Körper entsteht, wenn
man von platonischen Körpern passend alle Ecken entfernt.
Ein Beispiel ist der abgestumpfte
Würfel.
Das kleine Rhombenkuboktaeder
entsteht aus einem Würfel, wenn alle Kanten passend abgeschnitten
werden. |
Vorgehen
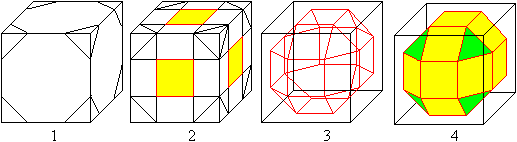1 Schräge die Kanten eines Würfels so ab, dass
die Quadrate zu regelmäßigen Achtecken werden.
2 Zerlege die Achtecke in Quadrate und Dreiecke. Drei
gelbe Zentralquadrate des kleinen
Rhombenkuboktaeders
auf
den Würfelflächen erkennt man schon.
3 Lösche alle überflüssige Linien. Es
bleibt das kleine Rhombenkuboktaeder übrig.
4 Mit Farbe und ohne Durchsicht
wird der Körper deutlicher.
Aus den 8 Ecken des Würfels
werden Dreieckseiten.
Die 12 Mitten der Kanten werden zu Quadraten.
Die 6 quadratischen Seitenflächen
des Würfels werden reduziert zu kleinen Quadraten.
Vom Oktaeder zum kleinen Rhombenkuboktaeder
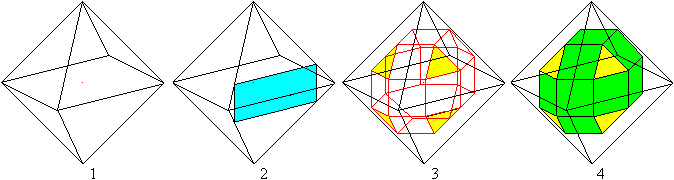Man kann das Rhombenkuboktaeder auch
aus einem Oktaeder gewinnen.
1 Gehe aus von einem Oktaeder.
2 Schräge alle Kanten passend
ab, so wie an einer Kante angedeutet.
3 Lösche alle überflüssige Linien. Es
bleibt das Rhombenkuboktaeder übrig.
4 Mit Farbe und ohne Durchsicht
wird der Körper deutlicher.
Die
8 dreieckigen Seitenflächen des Oktaeders werden reduziert zu kleineren
Dreiecken.
Die 8 Ecken des Oktaeders
werden abgeschnitten und werden zu Quadraten.
An den 12 Mitten der Kanten entstehen nach dem Abschrägen
auch Quadrate.
Größen top
Das Rhombenkuboktaeder sei
durch die Kantenlänge a gegeben.
Daraus lassen sich weitere Größen wie Radius
R
der Umkugel, Radius
rk der Kantenkugel, Volumen V,
Oberfläche O, Abstand
d3 der Dreiecke und
Abstand d4 der Quadrate berechnen.
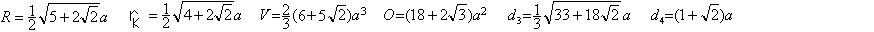
Oberfläche O
Die Oberfläche setzt sich
aus den Flächeninhalten der 18 Quadrate und der 8 Dreiecke zusammen.
O = 18A4+8A3 =
18a²+8*[(1/4)sqrt(3)a²] = [18+2sqrt(3)]a², wzbw.
Radius R
der
Umkugel
... ... |
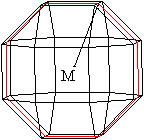Legt man durch die Mittellinie eines Ringes aus acht
Quadraten eine Schnittebene, so erhält man ein regelmäßiges
Achteck.
Der Mittelpunkt des Achtecks ist gleichzeitig Mittelpunkt
des kleinen Rhombenkuboktaeders. |
... ... |
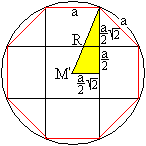Den Radius der Umkugel findet man
in einem rechtwinkligen Dreieck.
Es gilt nach dem Satz des Pythagoras
R² = [a/2+(a/2)sqrt(2)]²+[a/2sqrt(2]² =...
und weiter R = (1/2)sqrt[5+2sqrt(2)]a,
wzbw.. |
Radius
rk der Kantenkugel
Bei archimedischen Körpern liegen die Kantenmitten
auf einer Kugel, der Kantenkugel.
 |
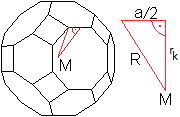Der Radius rk der Kantenkugel kann über
den Radius R der Umkugel bestimmt werden.
Im rechtwinkligen Dreieck gilt rk² =
R²-[(1/2)a]² = (1/4)[5+2sqrt(2)]a²-(1/4)a² = (1/4)[4+2sqrt(2)]a².
Dann ist rk= (1/2)sqrt[4+2sqrt(2)]a, wzbw. |
Abstand
d4
der
Quadrate
Der Abstand gegenüberliegender Quadrate ist in der
obigen Zeichnung als Kantenlänge des erzeugenden Würfels unmittelbar
abzulesen: d4 = a+sqrt(2)a = [1+sqrt(2)]a, wzbw..
Abstand d3
der
Dreiecke
... ... |
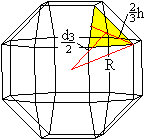Man kann in das Rhombenkuboktaeder
ein rechtwinkliges Dreieck legen, in dem die gesuchte Strecke (1/2)d3
Kathete ist. Die andere Kathete der Radius des Umkreises des gleichseitigen
Dreiecks. Der Radius der Umkugel ist die Hypotenuse.
Es gilt (d3/2)²
= R²-[(2/3)h]² = {(1/2)sqrt[5+2sqrt(2)]a}²-{(2/3)(1/2)sqrt(3)a}²
oder
d3² = (1/9)[33+18sqrt(2)]a²
oder d3 = (1/3)sqrt[33+18sqrt(2)]a, wzbw.. |
Volumen
V
Verbindet man die Eckpunkte des Rhombenkuboktaeders
mit dem Mittelpunkt, so wird es in Pyramiden zerlegt. Für das Volumen
gilt
V = 18*(1/3)a²(d4/2)+8*(1/3)(1/4)sqrt(3)a²(d3/2)={3+3sqrt(2)+(1/3)sqrt[11+6sqrt(2)]}a³
=...
= (2/3)sqrt[6+5sqrt(2)]a³,
wzbw..
Ein Winkel
Ferner gilt nach (1), Seite 105: Der Winkel zwischen
einer Dreieck- und Fünfeckfläche ist 135°44'.
Weitere Körper top
Deltoidalikositetraeder
... ... |
Verbindet man die Mittelpunkte benachbarter Seitenflächen
des kleine Rhombenkuboktaeders, so entsteht
der duale Körper, das Rhombentriakontaeder. |
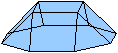
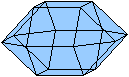
Quadratkuppel
... ... |
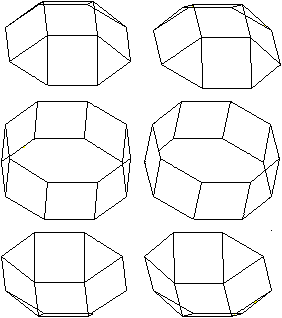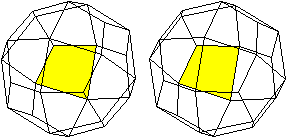
Das Rhombenkuboktaeders kann man
in zwei "Quadratkuppeln" und ein achtseitiges Prisma zerlegen.
Die Quadratkuppel besteht aus regelmäßigen
Vielecken, nämlich einem Achteck, 5 Quadraten und 4 Dreiecken.
Sie gehört zu den Johnson-Körpern, J4.
|
Die Quadratkuppel ist Bestandteil der Johnson-Körper
(J4), J19, J23, J28, J29, J37 und J45.
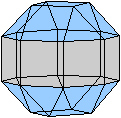
Verlängertes
verdrehtes Quadratsdoppelkuppel
J 37 (oder verdrehtes kleines Rhombenkuboktaeder)
Man erhält diesen Körper, indem man beim Rhombenkuboktaeder
eine Kappe entfernt, um 45° dreht und wieder aufsetzt.
... ... |
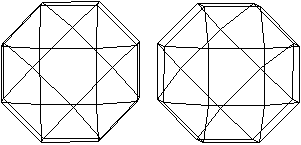Man könnte meinen, dieser Körper sei eine Variation
des kleinen Rhombenkuboktaeders, denn er hat die gleichen Daten:
8 Dreiecke, 18 Quadrate, (3,4,4,4), f=26, e=24,
k=48.
An jeder Ecke treffen ein Dreieck und drei Quadrate aufeinander. |
|
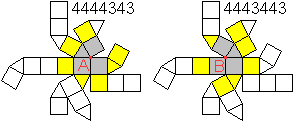
Betrachtet man das Netz der "verlängerten
verdrehten Quadratsdoppelkuppel", so ist zwar die Umgebung zweier Punkte
A
und B gleich (ein Dreieck, drei Quadrate), aber die weitere Umgebung zeigt
Unterschiede: Um A liegen vier aufeinander folgende Quadrate zwischen zwei
Dreiecken, um B höchstens drei. |
Rubik's
Snake
.. .... |
Das nebenstehende Puzzle
"Rubik's Snake" gehört zur Rubik's Cube Familie.
So sieht es beim Kauf aus. Er hieß
früher
Zauberschlange.
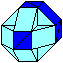
Man könnte meinen, es sei ein
kleines Rhombenkuboktaeder.
Aber es besteht aus Halbwürfeln
und deshalb ist das dunkelblaue Viereck zwar ein Quadrat, nicht aber die
anliegenden Vierecke. Es sind Rechtecke der Form 1:sqrt(2). |
.... .. |
Entwirrt man das Puzzle, erhält man eine Stange
aus 24 Halbwürfeln. |
... ... |
Basteln
eines Rhombenkuboktaeders top
|
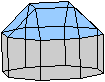
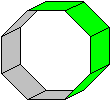
Acht Quadrate bilden einen Ring.
Es gibt drei Ringe dieser Art, die in die drei Richtungen
des Raumes zeigen. |
... ... |
Ein Ring lässt sich aus Papier bauen.
Drei Ringe lassen sich so ineinander stecken, dass sie
einen kleinen Rhombenkuboktaeder bilden, bei dem
die Dreiecksflächen als Löcher bleiben.
Das macht das Modell interessant. |
Kleines
Rhombenkuboktaeder im Internet top
Deutsch
Wikipedia
Rhombenkuboktaeder,
Deltoidalikositetraeder,
Archimedischer
Körper, Catalanischer
Körper, Herrnhuter
Stern, Nationalbibliothek
von Weißrussland
Englisch
Eric W. Weisstein (MathWorld)
Small
Rhombicuboctahedron, Dual: Deltoidal
Icositetrahedron, Archimedean
Solid
Geneviève Tulloue ( Figures Animées pour
la Physique )
Polyhedra
(Applets)
Gijs Korthals Altes
Paper
Model Rhombicuboctahedron
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programms.
Wikipedia
Rhombicuboctahedron,
Archimedean
solid,
Catalan
solid, Deltoidal
icositetrahedron
Rhombicuboctahedron
by Leonardo da Vinci, The
National Library of Belarus
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2007,
überarbeitet 2013, Jürgen Köller
top |
