|
What is the Sonobe Star?
... ... ... |
The Sonobe star is a three-dimensional star that is assembled
from 30 modules.
The modules are folded from squares.
Mathematically, it is an icosahedron with 20 three-sided
pyramids on its sides.
The name goes back to the Japanese origami enthusiast
Mitsunobu Sonobe. |
...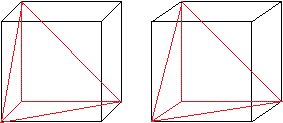 ... ... |
The pyramids are more exactly right-angled three-sided
pyramids. .................................
They occur at one corner of a cube.
Three congruent right-angled isosceles triangles meet
at the top.
The base is an equilateral triangle. |
... ... ... |
The Sonobe star is related to the Bascetta
Star, which is also a stellated icosahedron and which is also assembled
from 30 modules. |
Folding
of the Sonobe Module top
... ... ... |
You need 30 squares of paper for the star.
You can use the 9cm x 9cm note paper that you can
buy in stationery shops, for example. |
Nine
steps
1
...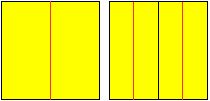 ... ... |
Divide the square sheet into four equal lengthwise strips
by folding three times.......

|
2
...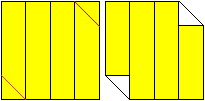 ... ... |
Fold on the red lines and you get the right figure................................................
 |
3
... ... ... |
Fold on the red lines and you get the right figure......................... |
4
...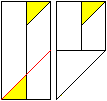 ... ... |
Fold on the red lines and you get the right figure. |
5
...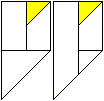 ... ... |
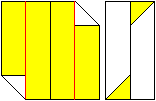
Undo the fold and tuck the lower
right triangle under the left longitudinal strip.........
This should look like the figure
on the right. |
6
...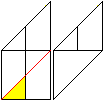 |
Turn the sheet 180° and fold on the red line. You
get the figure on the right. |
7
...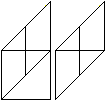 |
Undo the fold and tuck the lower right triangle under
the left longitudinal strip.
You get the right figure. |
8
...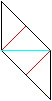 ... ... |
 |
Turn the figure over.
Fold on the red lines and on the blue line.
Unfold again. |
9
... |
This is the Sonobe module.
 |
Folding of
the Sonobe Star top
... ... ... |
You need 30 modules for the Sonobe star.
Don't worry, the module is easy to fold. |
... ... ... |
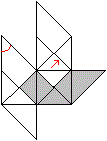 |
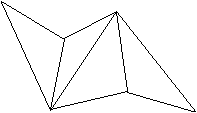
First you put three modules into each other and form
a pyramid corner
by pushing the tip marked in red into a pocket. |
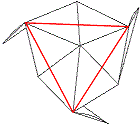
... ... ... |
This is the view of the pyramid corner............................................................................
 |
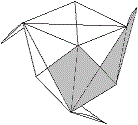
... ... ... |
Fold along the red lines to form a right-angled pyramid
with an equilateral triangle as its base. |
The
modules are added to the first pyramid one after the other until the star
finally closes.
...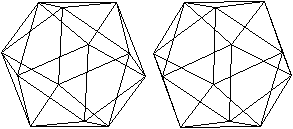 ... ... |
It is a great help in the resulting confusion if you
imagine the generating
icosahedron: Five triangles meet at each vertex.
For the star, this means that five pyramids always form
a wreath. |
... ... ... |
You can also see this in the photo of the finished star.
 |

Klasse VAB 2S der Justus-von-Liebig-Schule in Mannheim,
2015
More
3D-figures top
Folding of an octahedron star
...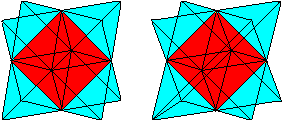 ... ... |
The octahedron star is created by placing tetrahedra
on the eight sides of an octahedron. |
...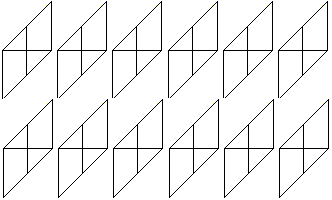 ... ... |
For a variant of the octahedron star you need 12 modules.
The tetrahedra become right-angled three-sided pyramids. |
... ... ... |
This is the star.
It is put together like the Sonobe star.
You just have to make sure that not five pyramids but
four pyramids form a wreath. |
Folding
of a Sonobe Cube
...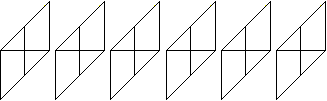 ... ... |
You need six modules for one cube.
 |
... ... ... |
 |
First you put three modules into each other and form
a cube corner,
by pushing the tip marked in red into a pocket. |
... ... ... |
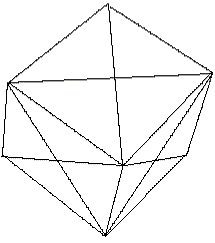
This is the view of a cube corner.
You add the three remaining modules one after the other
and finally arrive at the Sonobe cube. |
... ... ...
|
|
Construction
of a stellated cuboctahedron
...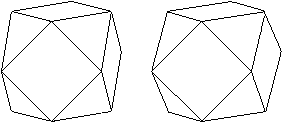 ... ... |
The cuboctahedron is an Archimedean solid formed by eight
equilateral triangles and six squares. The Sonobe modules allow it to be
stellated. |
... ... ... |
If you rebuild this figure from 24 modules, the result
is disappointing. It is similar to a cube, because the square pyramids
are very flat. |
Playing
with cubes
... |
Two cubes interpenetrate
Cube with double pyramid piggyback
Double cube |
Some Mathematics
top
..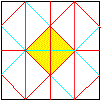 . . |
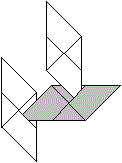
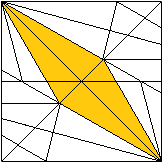
If you unfold the Sonobe module, a pattern of isosceles-rectangular
triangles emerges.
The triangle coloured yellow corresponds to the side
face of a right-angled pyramid. |
Two questions are of interest.
1
Only a small part of the surface of a module is used
for one pyramid. There are layers on top of each other.
What is the surface area O2 of the Sonobe
star in relation to the total area O1 of the 30 initial squares?
Calculation
Let a be the length of the square side, then the side
length of the basic triangle of a cone is (1/2)a.
The total area of all leaves is O1 = 30a².
The side area of a right-angled pyramid is (1/16)a².
The sum of all side areas or the surface area of the
star is then O2 = 20*3*(1/16)a² = (1/4)*15a².
The ratio O2:O1 is [(1/4)*15a²]:[30a²]
= 1/8 = 0.125 = 12.5 %.
Result
Only 12.5 % of the paper is used.
2
What is the size of the Sonobe star, if the initial square
has side length a.
The size of the star should be given by the distance
e of two opposite peaks.
Calculation
The distance is the sum of two heights H of the right-angled
pyramids and the distance d of opposite side faces of the icosahedron,
e = 2H+d.
On my website Three-Sided Pyramid you find H=(1/3)sqrt(3)*(1/2)a.
On my web page Bascetta Star you find d=(1/6)[3sqrt(3)+sqrt(15)](1/2)a.
That means e = (1/3)sqrt(3)a+(1/6)[3sqrt(3)+sqrt(15)](1/2)a
= [(5/12)sqrt(3)+(1/12)sqrt(15)]a = (1/12)[5sqrt(3)+sqrt(15)]a
or rounded e = 1.044a.
Result
If a is the side length of the square sheet of paper,
the Sonobe star is e = 1.044a.
If a= 9 cm, then e = 9.40 cm.
Variant of
the Sonobe Modul top
...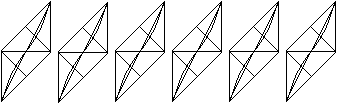 ... ... |
I know another variant of the Sonobe module that requires
an additional folding.
The module has the advantage that it is more stable.
Three modules form a bipyramid, six
a cube. - More details can be found via the two following
links. |
There is now (05/2022) another
web page on a stellated icosahedron made of 20 squares, the Kusudama
star.
Comparison
of three stars
|
a=9,0cm
|
Sonobe Star
|
Bascetta Star
|
Kusudama Star
|
|
2A/Aq
|
12,7%
|
20,0%
|
26,8%
|
|
H
|
0,29a = 2,6cm
|
0,49a = 4,4cm
|
0,70a = 6,3cm
|
|
e
|
1,04a = 9,4 cm
|
1,45a = 13,1cm
|
1,97a = 17,7cm
|
|
Sonobe Star
|
Bascetta Star
|
Kusudama Star
|

|
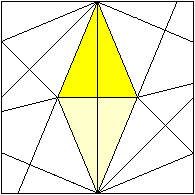
|
|
Sonobe Star
on the Internet top
German
greifswalderfalterstammtisch
Sonobe-Modul
(mit Somawürfel)
English
Origami-Resource-Center.com
Sonobe
Stellated Octahedron (12 units)
wikiHow
How
to Make a Sonobe Unit
Wikipedia
Sonobe
Youtube
Origami
Modular Sonobe Unit, Sonobe
instructions,
Youtube
DIY
- Stern Oktaeder Papier (Google Übersetzer)
Even though I couldn't understand the Russian commentator,
the octahedron star succeeded right away. The
pyramids are right-angled three-sided pyramids. That
is why this link appears on this page.
It is folded from a square sheet (cut to A4!) |

|
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2022 Jürgen Köller
top |

 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...

 ...
...
 ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
...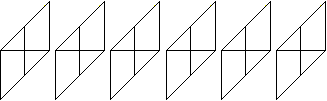 ...
... ...
...
 ...
... ...
...
 .
.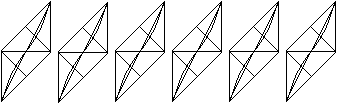 ...
...



